当前位置:网站首页>机械臂速成小指南(十六):带抛物线过渡的线性规划
机械臂速成小指南(十六):带抛物线过渡的线性规划
2022-08-02 15:10:00 【躺躺我啊】
🥰🥳需要机械臂相关资源的同学可以在评论区中留言哦
指南目录:
机械臂速成小指南(十八):圆弧规划
🦾🪐以下为正文🦾🪐
在上一章文末我们提到了线性规划的缺点:在起始点与终止点处存在速度的突变。因此,为了保证机械臂在起始与终止时的作业稳定性、安全性与精准性,我们使用抛物线对关节运动曲线进行过渡,这种关节空间轨迹规划方法称为带抛物线(parabolic)过渡的线性规划,使得关节角速度能以平滑的方式进行改变。
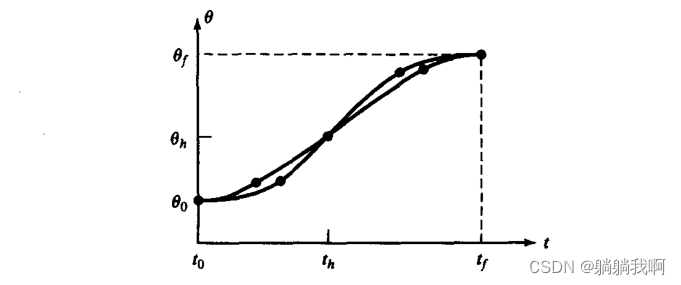
一、理论分析
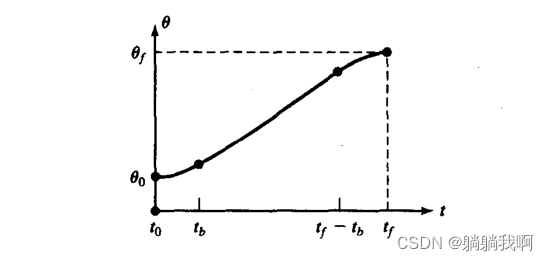
注:上图仅起到便于读者理解的作用,符号可能与下文不同
为便于计算,我们设起始拟合段与终止拟合段的持续时间一致,二者关于轨迹中点(t_mid,θ_mid) 中心对称,且拥有大小相等、符号相反的恒定角加速度。
设![]() 为抛物线拟合区域的角加速度,t_acc 为拟合区域的持续时间,θ_a 为起始拟合段终点角度值。由于起始拟合段终点的速度必须等于直线段的速度,则有
为抛物线拟合区域的角加速度,t_acc 为拟合区域的持续时间,θ_a 为起始拟合段终点角度值。由于起始拟合段终点的速度必须等于直线段的速度,则有
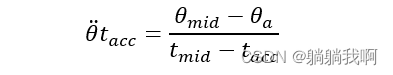
其中 ![]() 而θ_a 可表示为
而θ_a 可表示为
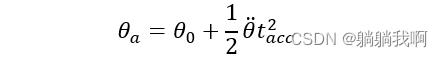
联立上方两个式子,我们可以得到
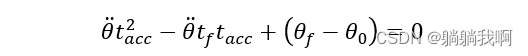
接着,求解t_acc ,得到
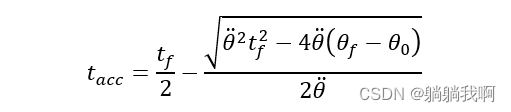
我们注意到,上式可解的条件是抛物线拟合区域的加速度![]() 满足
满足
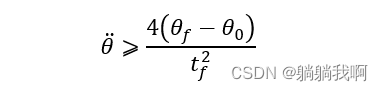
当上式等号成立时,关节运动曲线将不存在直线段,而是仅由两段抛物线组成;而当![]() 趋于无穷大时,所规划的关节运动曲线将重新变为一条直线,即回到线性规划的情况。
趋于无穷大时,所规划的关节运动曲线将重新变为一条直线,即回到线性规划的情况。
二、程序仿真
使用MATLAB对由抛物线过渡的线性插值的轨迹规划方法进行仿真。
第一步,定义机械臂的DH参数
%定义关节角度限制
lim1_min = -170 * radian1; lim1_max = 170 * radian1; %关节1(-170,170)
lim2_min = -132 * radian1; lim2_max = 0 * radian1; %关节2(-132,0)
lim3_min = 1 * radian1; lim3_max = 141 * radian1; %关节3(1,141)
lim4_min = -165 * radian1; lim4_max = 165 * radian1; %关节4(-165,165)
lim5_min = -105 * radian1; lim5_max = 105 * radian1; %关节5(-105,105)
lim6_min = -155 * radian1; lim6_max = 155 * radian1; %关节6(-155,155)
%定义关节旋转范围
lim1 = lim1_max - lim1_min;
lim2 = lim2_max - lim2_min;
lim3 = lim3_max - lim3_min;
lim4 = lim4_max - lim4_min;
lim5 = lim5_max - lim5_min;
lim6 = lim6_max - lim6_min;
%D-H参数表
theta1 = 0; d1 = 169.77; a1 = 64.2; alpha1 = -pi/2; offset1 = 0;
theta2 = 0; d2 = 0; a2 = 305; alpha2 = 0; offset2 = 0;
theta3 = 0; d3 = 0; a3 = 0; alpha3 = pi/2; offset3 = pi/2;
theta4 = 0; d4 = -222.63; a4 = 0; alpha4 = -pi/2; offset4 = 0;
theta5 = 0; d5 = 0; a5 = 0; alpha5 = pi/2; offset5 = 0;
theta6 = 0; d6 = -36.25; a6 = 0; alpha6 = 0; offset6 = -pi;
第二步,运动学建模
L(1) = Link([theta1, d1, a1, alpha1, offset1], 'standard');
L(2) = Link([theta2, d2, a2, alpha2, offset2], 'standard');
L(3) = Link([theta3, d3, a3, alpha3, offset3], 'standard');
L(4) = Link([theta4, d4, a4, alpha4, offset4], 'standard');
L(5) = Link([theta5, d5, a5, alpha5, offset5], 'standard');
L(6) = Link([theta6, d6, a6, alpha6, offset6], 'standard');
% 定义关节范围
L(1).qlim=[lim1_min,lim1_max];
L(2).qlim=[lim2_min,lim2_max];
L(3).qlim=[lim3_min,lim3_max];
L(4).qlim=[lim4_min,lim4_max];
L(5).qlim=[lim5_min,lim5_max];
L(6).qlim=[lim6_min,lim6_max];
robot = SerialLink(L,'name','AR3');第三步,定义起始点、终止点以及储存关节角度、角速度、角加速度的数组
T1=transl(-100,-100,300); %齐次变换矩阵
T2=transl(200,-200,400); %齐次变换矩阵
init_ang=robot.ikine(T1); %运动学逆解
targ_ang=robot.ikine(T2); %运动学逆解
q = zeros(step,N); %初始化机械臂的位置
qd = zeros(step,N); %初始化机械臂的角速度
qdd = zeros(step,N); %初始化机械臂的角加速度第四步,计算抛物线公式
step = 50; %总步长,也可看作总时间
t_mid = step / 2; %时间中点
t_acc = 10; %抛物线拟合段的持续步长(时间)
middle_ang = (targ_ang - init_ang) / 2 + init_ang; %计算角度中值
a_ang = init_ang + (targ_ang - init_ang) / 12; %定义起始抛物线拟合段的终点角度值
a_velocity = (middle_ang - a_ang) / (t_mid - t_acc); %终止抛物线拟合段的终点角速度值
acceleration = a_velocity / t_acc; %加速度第五步,进行轨迹规划
for t = 1:step
% 起始抛物线拟合段
if t <= t_acc
q(t,:) = acceleration * (t)^2 / 2 + init_ang; %位置
qd(t,:) = acceleration * t; %角速度
qdd(t,:) = acceleration; %角加速度
% 直线段
elseif (t > t_acc) && (t <= step - t_acc)
q(t,:) = a_velocity * (t - t_acc) + q(t_acc,:);%位置
qd(t,:) = a_velocity; %角速度
qdd(t,:) = 0; %角加速度
% 终止抛物线拟合段
else
q(t,:) = q(step - t_acc,:) + a_velocity * (t - (step - t_acc)) - acceleration * (t - (step - t_acc))^2 / 2;%位置
qd(t,:) = a_velocity - acceleration * (t + t_acc - step); %角速度
qdd(t,:) = -acceleration; %角加速度
end
end效果如下图所示
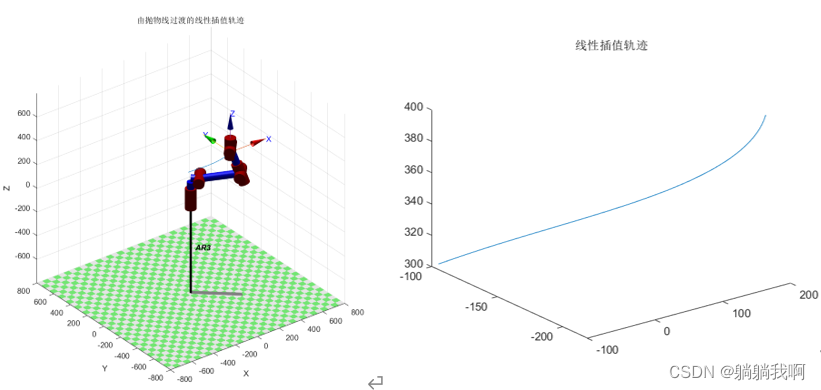
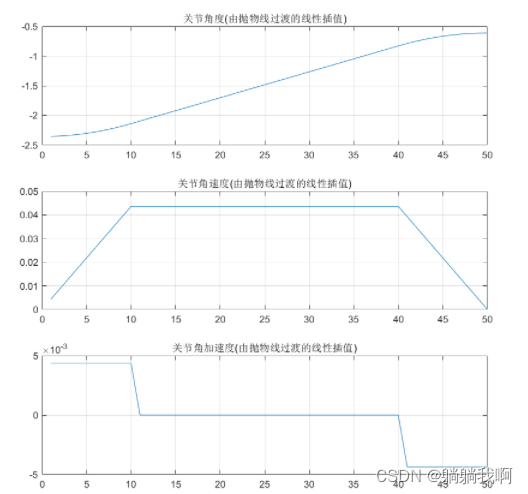
三、编程实现
机械臂在运行过程中较为平稳,且在作往复运动时,臂体振动幅度变小。

边栏推荐
猜你喜欢
随机推荐
2.5 - 死锁
QT | VS2017 + Qt5.14.2 环境搭建
入门关于 switch case 的理解
类的比较大小(Comparable -> compareTo(类自己实现接口),Comparator -> compare(新建一个类作为比较器))
IDO预售DAPP系统开发(NFT挖矿)
【个人总结】2022.7月结
23、wpf之布局(一)
数据防泄漏产品该如何选择
23.支持向量机的使用
该死的单元测试,写起来到底有多痛?
Qt | 关于 Qt Creator 打开项目编译不过的问题
从特征交互到数据交互,浅谈深度点击率模型的新趋势
先睹为快!界面控件DevExpress WPF这些功能即将发布
24、wpf之布局(二)
华为研究院19级研究员几年心得,终成趣谈网络协议文档,附大牛讲解
PAT serie a 1137 final grades
面试官的角度谈谈算法岗面试的过程(岗位涉及到OCR、目标检测、图像分割、语音识别等领域)
GFP-GAN学习笔记
UnicodeEncodeError: 'gbk' codec can't encode character '\u2022' in position 178: illegal multibyte s
ROS人机交互软件