当前位置:网站首页>[combinatorics] permutation and combination (set combination, one-to-one correspondence model analysis example)
[combinatorics] permutation and combination (set combination, one-to-one correspondence model analysis example)
2022-07-03 14:37:00 【Programmer community】
Arrange and combine reference blogs :
- 【 Combinatorial mathematics 】 Basic counting principle ( The principle of addition | Multiplication principle )
- 【 Combinatorial mathematics 】 Examples of permutation and combination of sets ( array | Combine | Circular arrangement | binomial theorem )
- 【 Combinatorial mathematics 】 Permutation and combination ( Arrange and combine content summary | Select the question | Set arrangement | Set combination )
- 【 Combinatorial mathematics 】 Permutation and combination ( Examples of permutations )
- 【 Combinatorial mathematics 】 Permutation and combination ( Multiset arrangement | Full Permutation of multiple sets | Multiset incomplete permutation The repetition of all elements is greater than the number of permutations | Multiset incomplete permutation The repetition of some elements is less than the number of permutations )
- 【 Combinatorial mathematics 】 Permutation and combination ( The combinatorial number of multiple sets | The repetition of all elements is greater than the number of combinations | The combinatorial number of multiple sets deduction 1 Division line derivation | The combinatorial number of multiple sets deduction 2 Derivation of the number of nonnegative integer solutions of indefinite equations )
- 【 Combinatorial mathematics 】 Permutation and combination ( Example of the number of combinations of multiple sets | Three counting models | Select the question | Multiple set combinatorial problem | Nonnegative integer solutions of indefinite equations )
- 【 Combinatorial mathematics 】 Permutation and combination ( Two counting principles 、 Set arrangement example | Set arrangement 、 Example of circle arrangement )
One 、 Set combination 、 One to one correspondence model analysis example
take
2
n
2n
2n Personal share
n
n
n Group , Each group
2
2
2 people , How many ways are there ?
First determine whether the problem is a selection problem , Is the element repeated , Whether the selection is orderly ,
- Non repeatable elements , Orderly selection , Corresponding Arrangement of sets
- Non repeatable elements , Unordered selection , Corresponding A combination of sets
- Repeatable elements , Orderly selection , Corresponding Arrangement of multiple sets
- Repeatable elements , Unordered selection , Corresponding Combination of multiple sets
2
n
2n
2n personal , People must not repeat , Divide into
n
n
n Group , There is no difference in the grouping here , Equivalent to the division of sets ;
There are also restrictions , Each group can only put
2
2
2 Elements ;
Original simple model , Such as classification ( Add ) , Step by step ( Multiplication ) , Set arrangement , Set combination , Multiset arrangement , Combination of multiple sets , There is no corresponding model , Cannot be used directly ;
It's not a simple selection problem ;
Here we need to consider Groups are different , There is no difference between groups Two cases ;
If there is a difference in grouping , Divide into
n
n
n Group , Put the first
1
1
1 Group , choose
2
2
2 personal , Put it again
2
2
2 Group , choose
2
2
2 personal ,
⋯
\cdots
⋯ The plan is It can be calculated ;
There is no difference in grouping , At this time, we need to observe There are differences in grouping and There is no difference between The difference between :
There is no difference in grouping , Get a way , Then on
n
n
n Groups are arranged in full , Yes
n
!
n!
n! There are two ways to arrange them , The number of schemes with different groups is obtained ;
There will be Number of schemes with different grouping And Grouping does not distinguish the number of schemes Establish a correspondence :
branch
Group
no
Yes
District
other
Fang
case
Count
×
n
!
=
branch
Group
Yes
District
other
Fang
case
Count
Grouping does not distinguish the number of schemes \times n! = Number of schemes with different grouping
branch Group no Yes District other Fang case Count ×n!= branch Group Yes District other Fang case Count
Number of schemes with different grouping It can be calculated , then Divide
n
!
n!
n! , You can get Number of schemes with no difference in grouping ;
There are differences in grouping , according to Step by step processing The plan :
① The first
1
1
1 Step : from
2
n
2n
2n Of the elements , selection
2
2
2 Elements , Yes
C
(
2
n
,
2
)
C(2n , 2)
C(2n,2) Kind of plan ;
② The first
2
2
2 Step : from
2
n
−
2
2n - 2
2n−2 Of the elements , selection
2
2
2 Elements , Yes
C
(
2
n
−
2
,
2
)
C(2n - 2 , 2)
C(2n−2,2) Kind of plan ;
③ The first
3
3
3 Step : from
2
n
−
4
2n - 4
2n−4 Of the elements , selection
2
2
2 Elements , Yes
C
(
2
n
−
4
,
2
)
C(2n - 4 , 2)
C(2n−4,2) Kind of plan ;
⋮
\vdots
⋮
④ The first
n
n
n Step : from
2
n
−
(
2
n
−
2
)
2n - ( 2n - 2 )
2n−(2n−2) Of the elements , selection
2
2
2 Elements , Yes
C
(
2
n
−
(
2
n
−
2
)
,
2
)
C(2n - ( 2n - 2 ) , 2)
C(2n−(2n−2),2) Kind of plan ; That is to say
1
1
1 Kind of plan ;
Permutation and combination formula
- array :
P
(
n
,
r
)
=
n
!
(
n
−
r
)
!
P(n,r) = \dfrac{n!}{(n-r)!}
P(n,r)=(n−r)!n!
- Combine :
C
(
n
,
r
)
=
P
(
n
,
r
)
r
!
=
n
!
r
!
(
n
−
r
)
!
C(n, r) = \dfrac{P(n,r)}{r!} = \dfrac{n!}{r!(n-r)!}
C(n,r)=r!P(n,r)=r!(n−r)!n!
Step by step processing You need to use the multiplication principle , take
n
n
n Multiply the number of schemes in steps :
N
=
C
(
2
n
,
2
)
C
(
2
n
−
2
,
2
)
C
(
2
n
−
4
,
2
)
⋯
C
(
2
n
−
(
2
n
−
2
)
,
2
)
=
2
n
!
2
!
×
(
2
n
−
2
)
!
×
(
2
n
−
2
)
!
2
!
×
(
2
n
−
4
)
!
⋯
(
2
n
−
(
2
n
−
2
)
)
!
2
!
×
(
2
n
−
(
2
n
−
2
)
−
2
)
!
⏟
n
individual
branch
Step
phase
ride
front
after
can
With
about
fall
very
many
rank
ride
=
(
2
n
)
!
(
2
!
)
n
\begin{array}{lcl} N &=& C(2n , 2) C(2n - 2 , 2) C(2n - 4 , 2) \cdots C(2n - ( 2n - 2 ) , 2) \\\\ &=& \begin{matrix} \underbrace{ \cfrac{2n!}{2! \times (2n-2)!} \times \cfrac{(2n-2)!}{2! \times (2n-4)!} \cdots \cfrac{(2n - ( 2n - 2 ))!}{2! \times (2n - ( 2n - 2 ) - 2)!} } \\ n Multiply by steps \end{matrix} Many factorials can be reduced before and after \\\\ &=& \cfrac{(2n)!}{(2!)^n} \end{array}
N===C(2n,2)C(2n−2,2)C(2n−4,2)⋯C(2n−(2n−2),2)
2!×(2n−2)!2n!×2!×(2n−4)!(2n−2)!⋯2!×(2n−(2n−2)−2)!(2n−(2n−2))!n individual branch Step phase ride front after can With about fall very many rank ride (2!)n(2n)!
The number of schemes with different grouping is
(
2
n
)
!
(
2
!
)
n
\cfrac{(2n)!}{(2!)^n}
(2!)n(2n)! individual ;
according to
branch
Group
no
Yes
District
other
Fang
case
Count
×
n
!
=
branch
Group
Yes
District
other
Fang
case
Count
Grouping does not distinguish the number of schemes \times n! = Number of schemes with different grouping
branch Group no Yes District other Fang case Count ×n!= branch Group Yes District other Fang case Count
The formula ;
Number of schemes with different grouping It can be calculated , then Divide
n
!
n!
n! , You can get Number of schemes with no difference in grouping ;
The end result is
(
2
n
)
!
(
2
!
)
n
n
!
\cfrac{(2n)!}{(2!)^n n!}
(2!)nn!(2n)!
This problem is not simple to use Original simple model , Such as classification ( Add ) , Step by step ( Multiplication ) , Set arrangement , Set combination , Multiset arrangement , Combination of multiple sets ;
Instead, it will be an Uncomputable model , Corresponding to a computable model , Then calculate the model The repeatability of
边栏推荐
- Similarities and differences between Allegro, OrCAD, net alias, port, off page connector and how to select them
- How to query the baby category of tmall on Taobao
- 洛谷P3065 [USACO12DEC]First! G 题解
- 7-10 stack of hats (25 points) (C language solution)
- Add ZABBIX calculation type itemcalculated items
- Code writing and playing method of tonybot humanoid robot at fixed distance
- 7-3 rental (20 points)
- String reverse order
- Table of mathematical constants by q779
- 分布式事务(Seata) 四大模式详解
猜你喜欢

Four data flows and cases of grpc
![洛谷P4047 [JSOI2010]部落划分 题解](/img/7f/3fab3e94abef3da1f5652db35361df.png)
洛谷P4047 [JSOI2010]部落划分 题解
ShowMeBug入驻腾讯会议,开启专业级技术面试时代

Showmebug entered Tencent conference, opening the era of professional technical interview

提高效率 Or 增加成本,开发人员应如何理解结对编程?
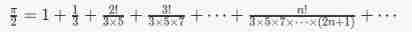
7-15 calculation of PI

Sword finger offer 28 Symmetric binary tree
![[qingniaochangping campus of Peking University] in the Internet industry, which positions are more popular as they get older?](/img/f6/fe61c84f289f0e74a45946dac687a6.jpg)
[qingniaochangping campus of Peking University] in the Internet industry, which positions are more popular as they get older?
分布式事务(Seata) 四大模式详解

Detailed explanation of four modes of distributed transaction (Seata)
随机推荐
编程语言:类型系统的本质
Understand the application scenario and implementation mechanism of differential segment
Dllexport and dllimport
Zzuli:1044 failure rate
7-24 reduction of the simplest fraction (rolling Division)
Sendmail无法发送邮件及发送过慢解决
dllexport和dllimport
Luogu p5194 [usaco05dec]scales s solution
FPGA blocking assignment and non blocking assignment
关于敏捷的一些概念
Thread.sleep和TimeUnit.SECONDS.sleep的区别
Common shortcut keys in PCB
Zzuli:1043 max
Showmebug entered Tencent conference, opening the era of professional technical interview
Creation of data table of Doris' learning notes
Zzuli:1056 lucky numbers
Programming language: the essence of type system
Zzuli:1049 square sum and cubic sum
Detailed explanation of four modes of distributed transaction (Seata)
Add ZABBIX calculation type itemcalculated items