当前位置:网站首页>【Day1/5 文献精读】Speed Constancy or Only Slowness: What Drives the Kappa Effect
【Day1/5 文献精读】Speed Constancy or Only Slowness: What Drives the Kappa Effect
2022-06-11 22:50:00 【余阿Adzuki】
阅读文献:
Chen Y, Zhang B, Kording KP (2016) Speed Constancy or Only Slowness: What Drives the Kappa Effect. PLoS ONE 11(4): e0154013. doi:10.1371/journal.pone.0154013
文献链接:Speed Constancy or Only Slowness: What Drives the Kappa Effect
文章目录
摘要
什么是Kappa效应:空间距离对时间知觉的影响
两个模型假设:经典模型(恒定速度)VS贝叶斯模型(慢速度先验)
→本文的视觉实验发现:
1)在拟合数据时两种模型都能复制被试反应,但贝叶斯模型能更好预测行为;
2)估计的恒定速度接近于速度的绝对阈限;
3)Kappa效应是慢速度导致,并受空间变异性调节。
一、前言
1、Kappa效应解释:引用例子,当两物体以恒定时距相继出现时,其空间间隔越大知觉到的时间间隔越大。
2、经典模型(Classical model)介绍:物体在背景中以恒定速度移动,知觉到(估计)两物体出现的时间间隔(estimated time) te由样本时间间隔(sample time) ts与期望时间E(t)(给定距离l/恒定速度v0)加权(权重为ω)得:
![]() ( Eq1)
( Eq1)
然而,ω是未知的。
3、贝叶斯模型(Bayesian model,文中也表述为慢速度模型Slowness model)介绍:物体在背景中以慢速度移动,在系列触觉的时空知觉任务中已重现Kappa效应,但其能否解释视觉Kappa效应还有待验证。
4、本文提出:
贝叶斯模型中:后验的均值=先验与似然性均值的加权平均;
经典模型中:知觉到的时间=实际时间与期望时间的加权平均;
→ 这也许表明:在合适的定义下,经典模型也可以被表述为贝叶斯模型的形式。
5、本文假设:被试认为物体是以恒定速度移动;
研究方法:用贝叶斯模型来表述慢速度模型和经典模型,进行时间复制任务来复现视觉Kappa效应
研究目的:探讨哪个模型能更好解释Kappa效应。
二、实验一
1、实验设计
9名被试参与17(两圆间水平距离)×2(两圆呈现时间间隔sample time interval,0.8s/1.2s)被试内实验设计,需按键复制两圆呈现的时间间隔(producted time) tp,每个处理40个trail共1360个trail。

2、贝叶斯模型
(1)对于经典模型:由其得到被试估计两圆出现的时间间隔 te的公式见Eq1.
将经典模型表述为贝叶斯模型的形式,过程如下:
贝叶斯模型的构建分为三阶段,由时间复制的理想观察者模型ideal observer model for time reproduction改进而来,如下图:
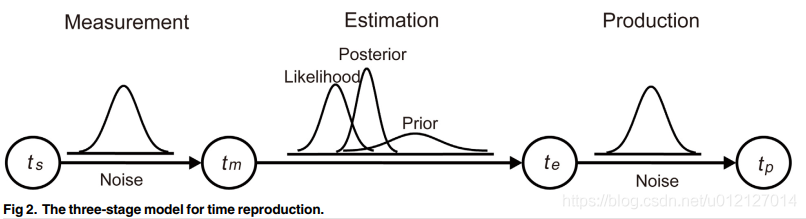
对此部分涉及到的符号和概念做个梳理:贝叶斯法则:
ts 样本时间sample time 样本实际呈现的时间间隔 tm 测量时间measured time(分布) 被试对样本时间间隔测得的时间,服从均值为ts标准差为σm的高斯分布,记为p(tm|ts),可视为感觉登记的时间/感觉记忆表征 te 估计时间estimated time 被试根据贝叶斯模型,结合prior与likelihood得到的估计时间,是posterior的均值,可视为知觉到的时间 tp 复制时间producted time(分布) 被试在反应阶段按键复制产生的时间分布,记为p(tp|te) prior 先验(分布) 对匀速运动物体的速度的先前经验,服从均值为l/v0标准差为στ的高斯分布,记p(τ) likelihood 似然性(分布) 服从均值为τ标准差为σm的高斯分布,记为p(tm|τ),τ为经验的时间也是个高斯分布。我认为likelihood本可以理解为根据经验时间τ得到的测量时间tm的分布。 posterior 后验(分布) 结合prior与likelihood得到的分布,均值为te
P(A|B)=P(B|A)*P(A)/P(B)
→也可改写为:后验概率 ∝ 似然性 * 先验概率 (∝代表两数成正比)
参考:无基础理解贝叶斯 - 夕月一弯 - 博客园
1)Measurement:样本时间间隔ts被被试所测量;在给定ts的条件下,被试测得的时间间隔tm的分布为p(tm|ts),其服从均值为ts标准差为σm的高斯分布。这与标量计时理论scalar timing theory一致(时距的内部表征是有精确平均值的多个值的分布)。
2)Estimation:被试对于移动物体的恒定速度v0有着先验信念,在给定移动距离l的条件下,被试会有一个先验的时间间隔分布p(τ),其服从均值为l/v0标准差为στ的高斯分布,如下: ( Eq2)
( Eq2)
似然性为 p(tm|τ),服从均值为τ标准差为σm的高斯分布,则后验分布可通过贝叶斯法则进行计算得:
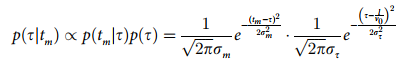 ( Eq3)
( Eq3)
后验分布的均值(被试估计的时间间隔 te)为:
 ( Eq4)
( Eq4)
参见Day 37阅读文献:Körding, K. P., & Wolpert, D. M. (2006). Bayesian decision theory in sensorimotor control. trends in cognitive sciences, 10(7), 319-326.
The combination (posterior) of likelihood and prior in Bayes’ rule is driven by their respective uncertainty (variance).
给定样本时间间隔ts,则被试估计的时间间隔 te为:
 ( Eq5)
( Eq5)
令 ![]() ,则有:
,则有:
 ( Eq6)
( Eq6)
可见,由贝叶斯模型计算被试估计的时间间隔 te的Eq6与经典模型计算 te的Eq1相等,说明Eq1可以被定义为一个贝叶斯模型。
3)Production:被试使用估计的时间间隔 te来按键复制产生tp,在给定te的条件下,tp的分布为p(tp|te)。以往研究表明(这里还需看下参考的文献),tp的标准差随其平均值线性增加,这一特性被称为标量变异性,即scalar variability。因此σp=wp*te,wp是一个韦伯分数Weber fraction,则有:
 ( Eq7)
( Eq7)
(2)对于慢速度模型:Goldreich用以复现触觉Kappa效应等而提出的一个基于慢速度假设的贝叶斯模型,被定义为中心为0的高斯分布函数,其推导出Kappa效应的公式Eq8。推导过程如下:
1)慢速度模型基于神经活动的概率分布,一个在皮肤上的触觉刺激将唤起一个神经反应D。给定初试触觉刺激的位置为x1,则起唤起的神经活动可以建模为空间位置x的函数,其服从均值为x1的高斯分布:
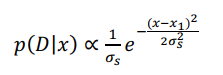 ( A7 )
( A7 )
2) 给定第二次触觉刺激的位置为x2,两次刺激间的速度和时距分别为v和τ,则第二次触觉刺激的神经概率分布为:
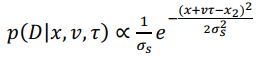 ( A8 )
( A8 )
4)神经活动也可以建模为时间t的高斯函数,中心为真实的触觉刺激施加的时间。第一次触觉刺激的真实施加时间定义为0,第二次的为ts(即两次刺激的时间间隔),则两次神经活动关于时间的高斯分布分别为:
 ( A9 )
( A9 )
 ( A10 )
( A10 )
5)在两次刺激间产生神经活动的似然性likelihood可写为空间x与时间t的概率分布:
 ( A11 )
( A11 )
6)慢速度先验prior反映了对慢速运动的期望,被建模为均值为0的高斯函数:
 ( A12 )
( A12 )
7)因而根据A11和A12,后验分布可使用贝叶斯法则进行计算:
![]()
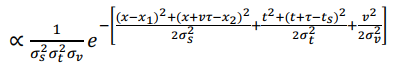 ( A13 )
( A13 )
8)将A13的指数对x、v、t和τ的偏导数设为0得到后验模式,感知到的时间te为后验模式下τ的值,则ts与te的关系式为(这一步还不太明白):
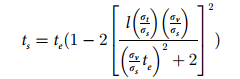 ( Eq8)
( Eq8)
其中,l为两刺激间距离,ts为样本时间间隔,te为被试估计的时间间隔,σs和σt分别为知觉到的空间和时间信息的标准差,σv为先验速度的标准差。
最后,被试使用te来按键复制两圆呈现的时间间隔tp,此过程与贝叶斯版本的经典模型中的第三步production一致。
3、将模型与数据进行拟合fitting
假设与任何ts相关的tp值在试验中是独立的。所有N个试次中个体的tp值的联合条件概率joint conditional probability为:
![]() ( Eq9)
( Eq9)
对数化后得:
![]() ( Eq10)
( Eq10)
(1)模型参数parameters:matlab中用最大似然法maximizing the likelihood确定,先前的研究表明ω是样本时间间隔的函数(这里还需看下参考的文献),故经典模型中有4个参数,ω0.8(0.8s时距条件中的权重)、ω1.2、v0和wp(韦伯分数);慢速度模型中也是4个参数,σt0.8、σt1.2、σv和wp。
(2)计算σs的方法(σs不是参数,可以计算获得)
1)最小可觉差JND(just noticeable difference):在心理测量功能上25%和75%之间的差异,标准差(σ)可以用JND计算得到一个高斯分布,即:
σ =JND/0.6475
2)视敏度阈值visual acuity threshold:为JND在视觉处理系统空间分辨率测量中的应用,先前研究报告了2种视敏度阈值(Vernier/grating resolutions)作为偏心度eccentricity的函数,分别为:
k = 0.93 ×ε^0.69 和 k = 1.34 × ε^0.71 (the unit of κ is minute not degree)
其中,κ为视觉敏锐度阈值(JND为空间分辨率),ε为偏心度。
3)因而有σs计算公式:
σs = 0.0239 × ε^0.69(Vernier resolution)和σs = 0.0345 × ε^0.71(grating resolution),(the unit of σs is degree not minute)
(3)Akaike information criterion (AIC):用来评估模型拟合程度的好坏
Δ = AICi-AICmin
其中,AICi来自第i个模型,AICmin来自最佳模型(AIC最小)。Δ越小代表该模型与最佳模型的差值越小,则模型拟合程度越好。
3、实验结果
(1)研究目的与方法:恒定速度和慢速度假设哪一种能最好地解释Kappa效应?在本实验设计中,被试复制产生的时间tp可以表述为两刺激空间距离和呈现时距的函数。
(2)反应偏差response bias (BIASr)
1)计算BIASr:在每种时间间隔下,两圆在注视点正上方30mm处的相同位置相继出现,被试复制时间tp的均值与标准时间间隔ts的差值即为BIASr。
2)单样本t检验One sample t-test:在0.8s时距条件下,BIASr显著>0(p<0.05);在1.2s时距条件下不显著。
3)BIASr的意义与矫正:BIASr代表着与刺激呈现空间距离无关的被试反应偏差,可作为一个基线baseline,尽管其值很小,作为矫正,在分析时将每个被试的复制时间都减去了其相对应的反应偏差。
(3)BIASk与VAR:在每种处理下,当两圆出现在相同位置时,BIASk为被试复制时间tp的均值与基线baseline的偏差值,VAR为其对应的方差,见下图:

1)BIASk随两圆的空间距离增大而增大(黑点与绿线距离从左到右呈增加趋势);
2)对于所有被试,VAR在0.8s时距条件下显著<1.2s时距(p<0.05)(A图中灰点比B图更集中),代表复制更长的样本时间有着更多的不确定性,这与标量变异性一致。
(4)拟合数据:经典模型和慢速度模型都能复现出被试的结果(拟合曲线与黑点基本重合),如下图:


1)经典模型:将生产时间预测为距离的线性函数。模型参数的均值,ω0.8和ω1.2非常接近1,v0约为0.2°/s, wp约为0.2,见下表:

2)慢速度模型:在0.8s时距条件下,估计时间在长距离时增速较短距离减缓,与慢速度模型结果更接近;在1.2s时距条件下,与两个模型结果都接近。在2种视敏度阈限值情况下,估计时间几乎相同(Fig 4B与4C中的拟合曲线几乎一致),且其最佳拟合参数值也几乎相等(下表), 在0.8s和1.2s时距条件下σt分别约为0.01s和0.02s,σv约为0.9°/s,wp约为0.2。

3)从Fig 4,慢速度模型似乎能更好地定性地解释数据(更好预测行为)。
(5)AIC difference (Δ):模型拟合程度的经验标准为0≤Δ ≤2, substantial; 4 ≤ Δ ≤7, considerably less; Δ >10, essentially none。结果见下表:

1)对于慢速度模型,在0.8s时距条件下,6个被试的拟合程度显著优于经典模型,而在1.2s时距条件下只有1个(表中标绿部分);
2)符号检验sign test表明,在0.8s时距条件下慢速度模型拟合度更好(p < 0.01),而1.2s时距条件下两个模型的拟合度差异不显著(p > 0.05)。
(6)模型的预测:使用最佳拟合参数the best-fitting parameters在更长的距离范围下对两模型的预测情况绘图如下(慢速度模型的视敏度阈限仅使用了Vernier resolution):

1)经典模型:复制时间随距离的增加而线性增加;
2)慢速度模型:复制时间随距离的增加而线性增加,但增速有着逐渐减缓的趋势;
3)两种模型间的差异随距离的增加而增加。这表明在今后的Kappa效应研究中,需要使用更大的距离范围。
三、实验二
在实验一中有个基本假设:被试在一种样本时间(两圆呈现时间间隔)中只有一种反应偏差。本实验旨在补充验证反应偏差是否受刺激呈现位置的影响。
1、实验设计
9名被试(与实验一不同)参与3(两圆位置相同,其与注视点的水平距离为左12°/0°/右12°)×2(两圆呈现时间间隔sample time interval,0.8s/1.2s)被试内实验设计,需按键复制两圆呈现的时间间隔,每个处理40个trail共240个trail。
2、实验结果
每个被试在每种时间间隔及每个呈现位置的反应偏差response biases (BIASr)的M和SE如下表:

对3种位置、2种时距做两因素重复测量设计方差分析Two-way repeated measurement ANOVA:时距、位置、时距和位置的交互作用的主效应main effects均不显著(p > 0.05),这表明刺激呈现位置对反应偏差无显著影响。
四、讨论
(1)在实验一中,通过比较模型拟合情况发现,基于恒定速度假设的经典模型和基于慢速度的慢速度模型都能复现被试的反应(Fig 4),但AIC指数表明慢速度模型能更好地拟合数据。
(2)关于本研究中发现的反应偏差response bias
1)之前没有关于视觉刺激呈现位置对于反应偏差是否产生影响的研究,本文在实验二中发现,结果为无显著影响;
2)在经典模型中,Jones and Huang提出在给定时距the given duration(ts),给定距离(l),Kappa效应计算(A4)分3步:
① 通过psychophysical function:φt,将ts转化为其scale value![]() :
:
![]() (A1)
(A1)
② 观测时间的内部编码internal code![]() 可以表述为scale value和期望时间expected time的加权形式:
可以表述为scale value和期望时间expected time的加权形式:
![]() (A2)
(A2)
其中,期望时间E(t)=l/v0,v0是恒定速度。
③ 通过psychomotor function:ht,利用internal code得到复制时间tp:
![]() (A3)
(A3)
Jones and Huang认为φt是线性的,可以令:
![]() 其中
其中![]() 代表偏差,则A2可写为:
代表偏差,则A2可写为:
![]() (A4)
(A4)
可以看出,Jones and Huang并未明确指出反应偏差。但在本研究的实验一中,通过将反应偏差进行定义:![]() ,把反应偏差从样本时间中实现分离(Fig 3),A4可写为:
,把反应偏差从样本时间中实现分离(Fig 3),A4可写为:
 (A5)
(A5)
将数据进行BIASr矫正后得到:
![]() (A6)
(A6)
A6与Jones and Huang得出的Kappa效应方程A4在数学上等价,但有更明确的心理学意义。
(3)模型拟合数据的2种方法
1)在拟合数据前对反应偏差进行矫正,确定基线水平。这也是本研究实验一中采用的方法。
2)将反应偏差作为模型的参数,对数据进行拟合。通过补充分析发现,此法使得两种模型的参数都由原来的4个增加为6个(新增BIASr0.8和 BIASr1.2,可见方程A5),这可能会在拟合部分被试数据时出现过度拟合overfitting现象。
(4)关于慢速度假设
1)慢速度模型:基于先验速度假设,且先验速度为慢速度,中心为0;
2)经典模型:也基于先验速度假设,且先验速度为恒定速度,逻辑上说,该恒定速度也可以是慢速度,理由如下:
① 由Fig 2,后验时间posterior的均值大于似然性likelihood的均值,则先验时间的均值一定大于似然性(因为后验由先验与似然性结合而来),也即先验速度比刺激圆闪现的速度要慢(v = l/t);在实验一中得到恒定速度v0约为0.2°/s,比圆闪现的速度要慢很多(1.2 to 28.3°/s);
② 以往研究表明,老年被试的绝对速度阈限为0.12°/s,青年被试为0.09°/s,与v0接近,故将恒定速度视为慢速度是合理的,这也是为什么经典模型和慢速度模型都复现了被试反应的原因(Fig 2);
③ 慢速度先验被证明反映了视觉环境的统计结构,即快速移动的物体相对较少,但其发生的神经机制需要进一步研究;
(5)两个模型拟合数据情况
1)从Fig 4,慢速度模型只在0.8s条件下呈现增速减缓趋势,1.2s条件没出现的原因是两圆的距离不够长仅1.4° to 22.6°。从Fig 5,距离增加到1.4° to 150°后,慢速度模型在1.2s条件下也出现了增速减缓趋势。
2)慢速度模型在长距离条件下呈现出增速减缓趋势,而经典模型为线性的,慢速度模型拟合数据能力更优。
3)为什么慢速度模型在长距离条件下呈现出增速减缓趋势?
→慢速度模型考虑到了空间变异性spatial variance,其值越大→离心率eccentricity越大→视觉敏锐度visual acuity越低→知觉到的距离越短→知觉到的时距越短
(6)两个模型的优缺点
1)经典模型
优点:基于一个简单的线性模型;
缺点:
① 拟合数据能力较差,未考虑空间信息的非线性特征(如空间变异性);
② 模型中的权重ω随样本时间的改变而改变,使模型无法用求得的最佳拟合参数来预测一个新的样本时间的复制时间。
2)慢速度模型
优点:基于神经活动的概率分布,考虑到了时空信息的不确定性,预测到复制时间随距离增加而呈增速减缓的趋势,拟合数据的能力更强;
缺点:
① 模型表达复杂,估计时间无法写为样本时间的函数te = f(ts),因此无法获得精确的te。
② 空间变异性的取值来自于先前研究的推算,且对各被试保持不变,但其可能会因为被试的个体差异、亮度对比等原因产生变化。
③ 时间信息的不确定性随样本时间的改变而改变,使模型无法用求得的最佳拟合参数来预测一个新的样本时间的复制时间。
因此,为了构建一个更好的Kappa效应模型,慢速度模型和经典模型的优缺点都应该考虑。
边栏推荐
- The second bullet of in-depth dialogue with the container service ack distribution: how to build a hybrid cloud unified network plane with the help of hybridnet
- Daily question -1317 Converts an integer to the sum of two zero free integers
- Exercise 8-2 finding a specified element in an array (15 points)
- Huawei equipment configuration hovpn
- Analysis of the implementation principle of an open source markdown to rich text editor
- The top ten trends of 2022 industrial Internet security was officially released
- Use the securecrtportable script function to read data from network devices
- 【NodeJs】Electron安装
- Four rounding modes in IEEE754 standard
- 完好性简要介绍
猜你喜欢

【Day13-14 文献精读】Cross-dimensional magnitude interactions arise from memory interference

Summary of personal wrong questions (the wrong questions have not been solved and are used for help)

Analysis of the implementation principle of an open source markdown to rich text editor

Fastapi 5 - common requests and use of postman and curl (parameters, x-www-form-urlencoded, raw)

leetcode 中的位运算
Want to be iron man? It is said that many big men use it to get started

How to do investment analysis in the real estate industry? This article tells you
![Tensorflow [actual Google deep learning framework] uses HDF5 to process large data sets with tflearn](/img/d0/586b9f09dc19d5aaf8ccca687b7b10.jpg)
Tensorflow [actual Google deep learning framework] uses HDF5 to process large data sets with tflearn
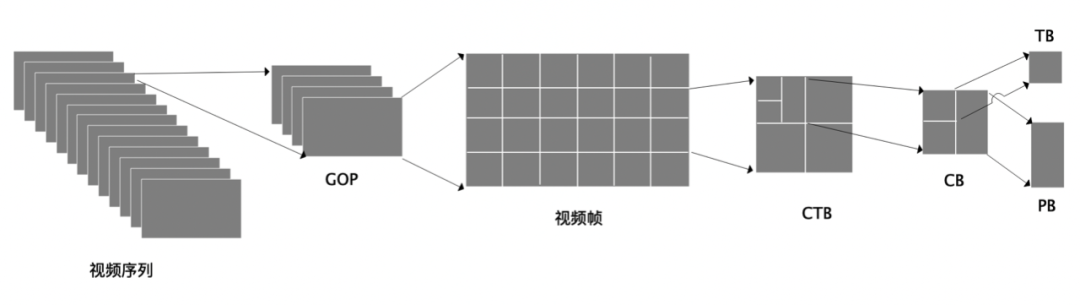
H. 265 introduction to coding principles

0-1 knapsack problem of dynamic programming (detailed explanation + analysis + original code)
随机推荐
R7-1 列表或元组的数字元素求和
Point cloud read / write (2): read / write TXT point cloud (space separated | comma separated)
习题8-5 使用函数实现字符串部分复制 (20 分)
阿里云服务器mysql远程连接一直连不上
JsonParseException: Unrecognized token ‘username‘: was expecting表单提交登陆数据报错
Svn deploys servers and cleints locally and uses alicloud disks for automatic backup
Matlab point cloud processing (XXV): point cloud generation DEM (pc2dem)
Research Report on development trend and competitive strategy of global reverse osmosis membrane cleaning agent industry
16 | floating point numbers and fixed-point numbers (Part 2): what is the use of a deep understanding of floating-point numbers?
astra pro双目相机ros下启动笔记
Gcache of goframe memory cache
Bit operation in leetcode
IEEE754标准中的4种舍入模式
Study notes of mattlotlib and Tkinter (I)
16 | 浮点数和定点数(下):深入理解浮点数到底有什么用?
0-1 knapsack problem of dynamic programming (detailed explanation + analysis + original code)
消息队列入门MQ
Read dense visual slam for rgb-d cameras
Exercise 9-5 address book sorting (20 points)
习题9-6 按等级统计学生成绩 (20 分)