Popular understanding of linear regression (II)

I have planned to present this series of blog posts in the form of animated interesting popular science , If you're interested Click here .

Digression ： stay Last one I talked about some concepts of linear regression and the form of loss function , Then this article will follow the idea of the previous one to talk about the solution of the normal equation of linear regression .（ If you are little white , You can click on the portal of the previous article to have a look , Maybe it can give you a general understanding of linear regression ）

3. How to calculate the solution of linear regression ？

Last one Finally, I talked about what the loss function is , The old ironmen who have understood it should have figured out a fact by now . That is, I just need to find a set of parameters （ That is, the coefficient of each term of the linear equation ） It can minimize the value of my loss function , Then my set of parameters can best fit my current training data .OK, How can I find this set of parameters ... In fact, there are two ways to find this set of parameters , One is the famous gradient descent , The general idea is to update the parameters according to the partial derivatives of each parameter to the loss function . The other is the normal equation solution of linear regression , The name sounds tall , In fact, it is to calculate the parameters according to a fixed formula . In this blog post , Mainly talk about the normal equation solution of linear regression , If the gradient decreases , The next blog post will be brought out alone to chat .

4. Solution of normal equation

The solution of a normal equation is actually a formula derived from a bunch of mathematical operations . Here, first give the final form of this formula , Then I broke it up and talked about how the goods came from .
Deng Deng Deng ... The whole length of this product is like this （ Among them θ, Is the parameter we need to calculate ）：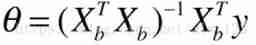

After the sacrifice of all , Let's see how this product grows from childhood to the end ...

When talking about the loss function of linear regression in the last article , We know that the loss function of linear regression is maozi ：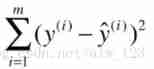

If we want to use linear regression to predict the house price of a city in China , In the formula y(i) It's in the training data label, That is, the real house price ,y^(i) It is the result predicted by our linear regression model , That is, the predicted house price . At the moment ,y(i) It's actually known . Because since it is supervised learning , That's the data label It's known . You can imagine the historical house price data of a city in China on a real estate trading platform , These data usually use the real house price at that time, right [/ funny ].

that y^(i) pinch ？ This is actually a linear expression , It looks like this ：

This formula is actually very easy to understand ,θ0 To θn It is the result of our request . If you only see θ0 To θ1 Part of the words , Nima is a linear equation （y=kx+b）, If you only see θ0 To θ2 Is that not a straight line in three-dimensional space .. That extends to θn When , That is to say n A line in dimensional space .

If we use the example of house price to explain this formula , It's better to understand . If X1 It represents the total area of the house ,X2 It represents the number of rooms in the house ,X3 It represents the building spacing ,X4 It represents the distance from school , Etc., etc. . At this time θ1 It represents the importance of the total area of the house to the house price , Then if θ1 It's a big number , That means the larger the total area of the house , The higher the house price . If θ1 be equal to 0, It means that the house price has nothing to do with the total area of the house .（ Other θ Please imagine for yourself ）

Now I have understood the meaning of this formula , But we found that this formula is too long , And if you throw it to GPU If you do the math ,GPU Will say :MMP, I'm not good at this . It's embarrassing ... So we might as well evolve this formula （ Yagu .. Ah bah .. Loss function evolution ...）.

If you receive the line agent , I guess you will have a conditioned reflex .... Is to see a formula that looks like the addition of a bunch of multiplication , I will immediately think of quantifying it . forehead , you 're right , The next step is to vectorize the smelly and long formula .

If we put θ0,θ1,θ2…θn Line up , That's actually a column vector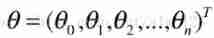

Again , If we put every attribute in a row of data , Or if each field lines it up , That's actually a row vector （ Superscript i Represents the... In the house price data i Data , Because you can't have only one historical data .0 To n Represents... In every piece of data 0 To n A field .PS:X0=1）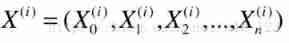

Then if we put Xi and θ Do a matrix multiplication , It's ours y^i Well

So! ,y^i It evolved into maozi ：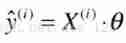

------------------------------------------- I'm the divider ----------------------------------------------

The evolution just done is just considering a piece of data in the data set , But when we calculate the loss function , We want to sum the loss values of all data . So! , We need to evolve a wave . If my house price characteristic data is long ：

The size of the house	Number of rooms	Floor spacing	Distance from school
60	2	10	5000
90	2	7	10000
120	3	8	4000
40	1	4	2000
89	2	10	22000

in other words X, Express

The size of the house	Number of rooms	Floor spacing	Distance from school
60	2	10	5000
90	2	7	10000
120	3	8	4000
40	1	4	2000
89	2	10	22000

that OK, Just now we know y^i Evolved into ：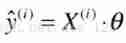

Now, if $x^i$ Line up , It becomes a matrix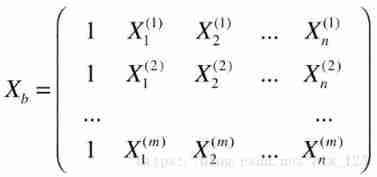

Which is equivalent to Xb It means

It doesn't matter	The size of the house	Number of rooms	Floor spacing	Distance from school
1	60	2	10	5000
1	90	2	7	10000
1	120	3	8	4000
1	40	1	4	2000
1	89	2	10	22000

If this time and θ If this column vector does matrix multiplication , Can handle y^ Evolved into mauve （ If you don't know why it can evolve like this .. Please preview matrix multiplication .. And please fill the shape of the result by yourself ）：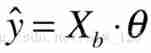

At the moment , You'll find that , Our formula for predicting house prices is very linear .. This is the origin of the name linear regression .

------------------------------------------- I'm the divider ----------------------------------------------

OJBK, We already know y^ What it looks like , Then we might as well look back at the loss function . The loss function looks like this ：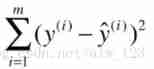

In fact, the loss function can also be vectorized , Because you can put all yi Line up into a column vector called y,y^i It is also a column vector called y ^. Then suppose y-y ^ This column vector is called U. Well, actually y-y ^ The sum of the squares of is U Sum of squares of . that U The sum of squares of can be imagined as U The transposition and U Do a matrix multiplication . So it is maozi after evolution ：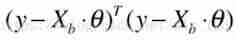

This is the time , What we have to do is very clear . because y It is known. ,Xb It is known. ,θ It is unknown. , That is to say, we need to solve θ, Let this equation hold . Next, let's see how to solve θ！！

------------------------------------------- I'm the divider ----------------------------------------------
This is the time , We can expand the formula first , After unfolding, it turns into dark purple （J(θ) The loss function ）：

Um. , Even if it is found, it will be expanded θ I still don't know how to calculate ... But if we calculate θ Yes J(θ) You know how to calculate the derivative of , because J(θ) We are looking for one θ（ At this moment θ It's a vector ） To minimize J(θ), So after derivation, we have the formula of maozi ：

Then move left and right to have ：

Then multiply both sides by X^TX The inverse of can get θ The expression of （θ All of you ）：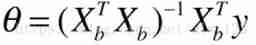

here , This is the normal equation solution of linear regression . That is to say, if you want to use linear regression to predict house prices , Directly set this formula, and you can get a set of parameters θ. With θ after , If you want to predict the possible house price of a new house data , Using this formula, you can predict the house price .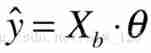

------------------------------------------- I'm the divider ----------------------------------------------
Only this and nothing more , Some things of linear regression have been finished . I hope this blog can help you when you read it . I haven't figured out what to write in the next article .. Maybe it's gradient descent ...