当前位置:网站首页>机器学习---线性回归、Logistic回归问题相关笔记及实现
机器学习---线性回归、Logistic回归问题相关笔记及实现
2022-07-31 06:24:00 【Miracle Fan】
回归问题
概述:
回归问题就是预测一个连续问题的数值,比如……,
而如果将上面的回归问题,利用Sigmoid函数(Logistic 回归),能将预测值变为判断是否能做某事情的概率,将回归得到的连续数值变为(0,1)之间的概率,然后可以用于处理二分类问题
一元线性回归
线性回归方程为:
y ^ = a x + b \hat{y} =ax+b y^=ax+b
比如给定一组数据,可以得到如下的散点图。
x=np.array([1,2,4,6,8])
y=np.array([2,5,7,8,9])

为了进行线性回归,相当于我们拟合出一条直线,能很好地去连接上图中各个样本,但是一般情况下是达不到完美的拟合效果的,只是希望如下图所示,绿色的线表示预测点与真实点之间的误差,我们希望误差尽可能的小,也就是能达到较好的拟合效果了。
y_pred=lambda x: a*x+b
plt.scatter(x,y,color='b')
plt.plot(x,y_pred(x),color='r')
plt.plot([x,x], [y,y_pred(x)], color='g')
plt.show()
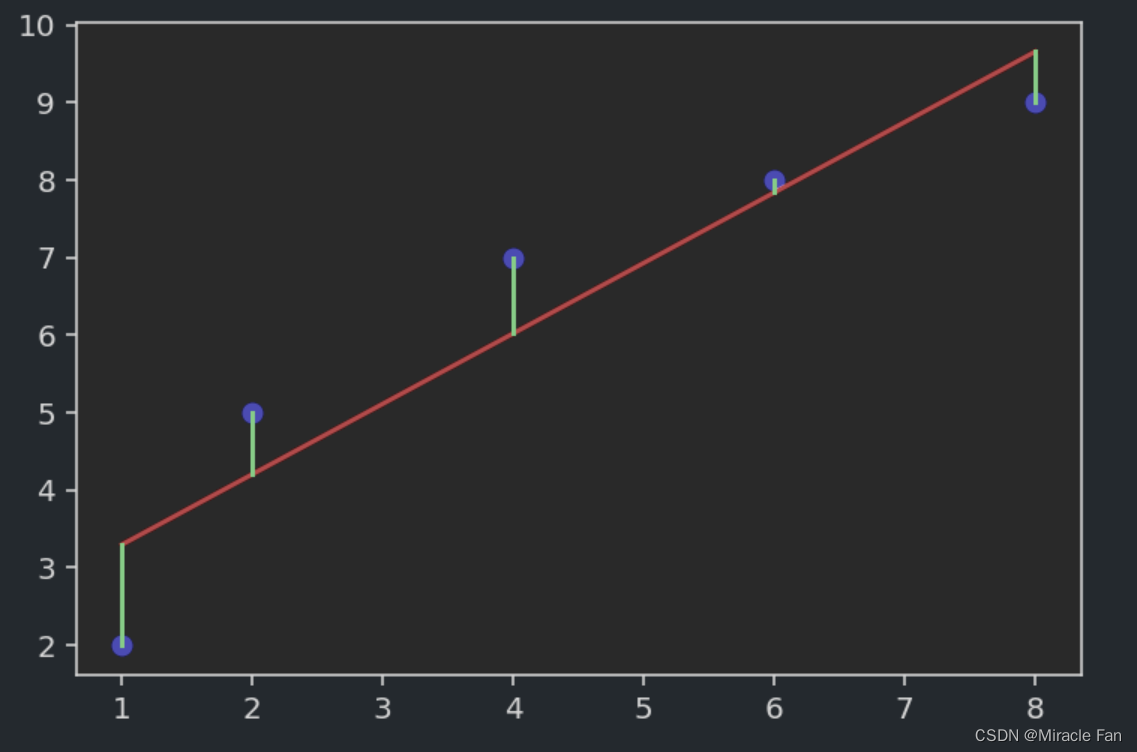
也就是可以定义一个损失函数:
L = 1 n ∑ i = 1 n ( y i − y p r e d i ) L=\frac{1}{n}\sum^n_{i=1}(y^i-y_{pred}^i) L=n1i=1∑n(yi−ypredi)
但是如果选用该函数,当我们进行误差计算时,某些情况下预测值大于真实值,某些情况下预测值小于真实值。则会导致 y − y p r e d y-y_{pred} y−ypred出现正、负的情况,而将他们相加的时候,则会导致相互抵消,所以这里我们需要采用均方损失函数:
L = 1 n ∑ i = 1 n ( y i − y p r e d i ) 2 L=\frac{1}{n}\sum^n_{i=1}(y^i-y_{pred}^i)^2 L=n1i=1∑n(yi−ypredi)2
代入拟合方程:
L = 1 n ∑ i = 1 n ( y i − a x i − b ) 2 L=\frac{1}{n}\sum^n_{i=1}(y^i-ax^i-b)^2 L=n1i=1∑n(yi−axi−b)2
利用最小二乘法推导法则:
a = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 b = y ˉ − a x ˉ a=\frac{\sum_{i=1}^n(x_i-\bar{x})(y^i-\bar{y})}{\sum_{i=1}^n(x^i-\bar{x})^2}\\ b=\bar{y}-a\bar{x} a=∑i=1n(xi−xˉ)2∑i=1n(xi−xˉ)(yi−yˉ)b=yˉ−axˉ
def Linear_Regression(x,y):
x_mean=np.mean(x)
y_mean=np.mean(y)
# num=np.sum((x-np.tile(x_mean,x.shape))*(y-np.tile(y_mean,y.shape)))
num=np.sum((x-x_mean)*(y-y_mean))
den=np.sum((x-x_mean)**2)
a=num/den
b=y_mean-a*x_mean
return a,b
由于numpy的广播机制,此处不必将x_mean的维度进行调整。
多元线性回归
对于多元线性回归,其一般表达式为:
y = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n y=\theta_0+\theta_1x_1+\theta_2x_2+\dots+\theta_nx_n y=θ0+θ1x1+θ2x2+⋯+θnxn
这个公式可以简化为:
Y = θ ⋅ X Y=\theta \cdot X Y=θ⋅X
X = ( 1 x 11 ⋯ x 1 p 1 x 21 ⋯ x 2 p ⋮ ⋮ ⋱ ⋮ 1 x n 1 ⋯ x n p ) X=\left(\begin{array}{cccc} 1 & x_{11} & \cdots & x_{1 p} \\ 1 & x_{21} & \cdots & x_{2 p} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n 1} & \cdots & x_{n p} \end{array}\right) X=⎝⎛11⋮1x11x21⋮xn1⋯⋯⋱⋯x1px2p⋮xnp⎠⎞
θ = ( θ 0 θ 1 θ 2 … θ n ) \theta=\begin{pmatrix} \theta_0\\ \theta_1\\ \theta_2\\ \dots \\ \theta _n \end{pmatrix} θ=⎝⎛θ0θ1θ2…θn⎠⎞
而对于 θ \theta θ的求解,利用于前文的最小二乘法,可以得到:
θ = ( X i T X i ) − 1 X i T y \theta=(X_i^TX_i)^{-1}X_i^Ty θ=(XiTXi)−1XiTy
#生成一列用于操作截距值
ones = np.ones((X_train.shape[0], 1))
#在horizental方向上进行堆叠
X_b = np.hstack((ones, X_train)) # 将X矩阵转为第一列为1,其余不变的X_b矩阵
theta = linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
interception = theta[0]
coef =theta[1:]
logistic回归
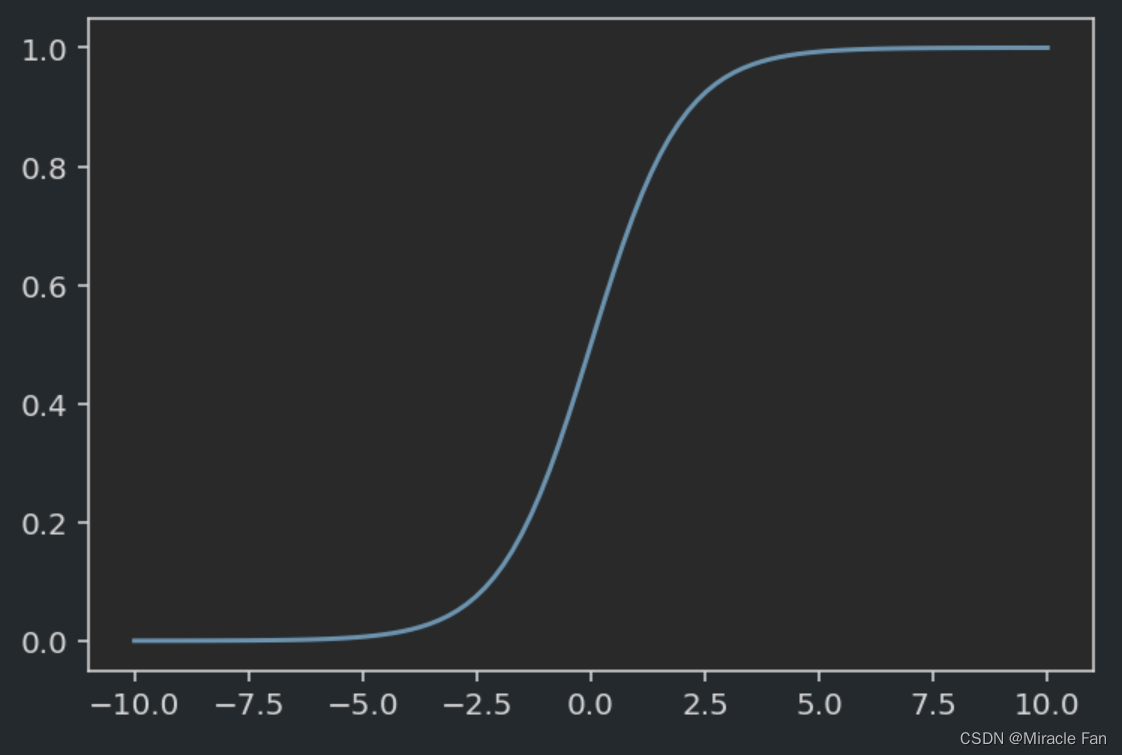
简单的logistics回归就是在线性回归的基础上加上Sigmoid函数,实现对预测结果的压缩,使之保持在(0,1)之间也就是可以理解成概率值,然后通常以0.5作为分界线,概率大于0.5则为类别1反之为0.
用于将利用线性回归得到的概率问题利用sigmoid函数输出为类别问题。
p = 1 1 + e − z p=\frac{1}{1+e^{-z}} p=1+e−z1
- z:一般为线性回归方程
- p:预测得到的概率,通过分界线判断属于哪一类
梯度下降
梯度下降法主要是应用在对损失函数的优化上,找到loss值最小的参数值。
比如假设一个损失函数为
L = ( x − 2.5 ) 2 − 1 L=(x-2.5)^2-1 L=(x−2.5)2−1
然后定义其损失函数及其导数。
def J(theta):
try:
return (theta-2.5)**2-1
except:
return float('inf')
def dJ(theta):
return 2*(theta-2.5)
每一次迭代
θ = θ + η d J θ \theta=\theta+\eta\frac{dJ}{\theta} θ=θ+ηθdJ
def CalGradient(eta):
theta = 0.0
theta_history = [theta]
epsilon = 1e-8#用于最终终止梯度下降的计算
while True:
gradient = dJ(theta)
last_theta = theta
theta = theta - eta * gradient
theta_history.append(theta)
if (abs(J(theta) - J(last_theta)) < epsilon):
break
plt.title('lr:' + str(eta))
plt.plot(x, J(x), color='r')
plt.plot(np.array(theta_history), J(np.array(theta_history)), color='b', marker='x')
plt.show()
print(len(theta_history))
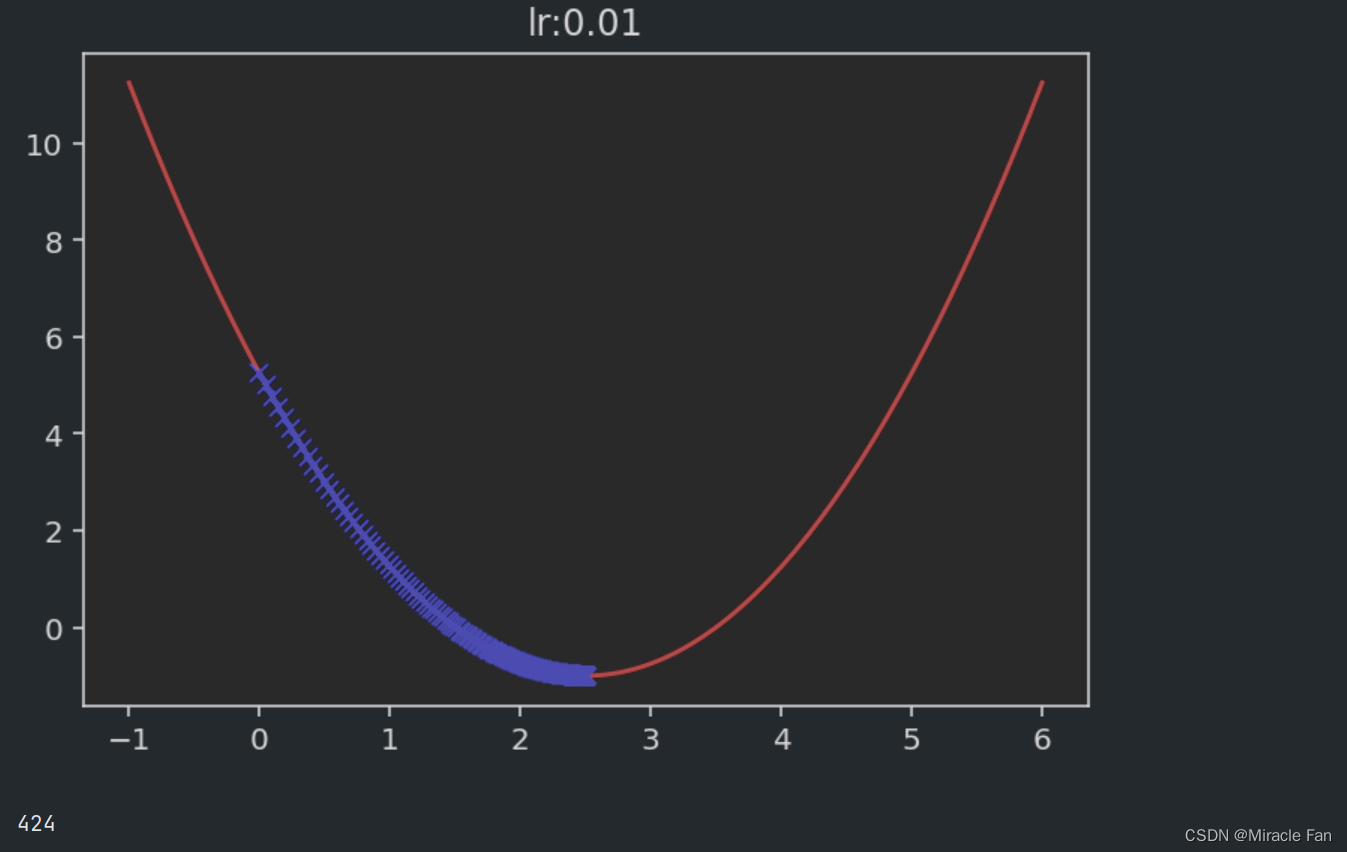
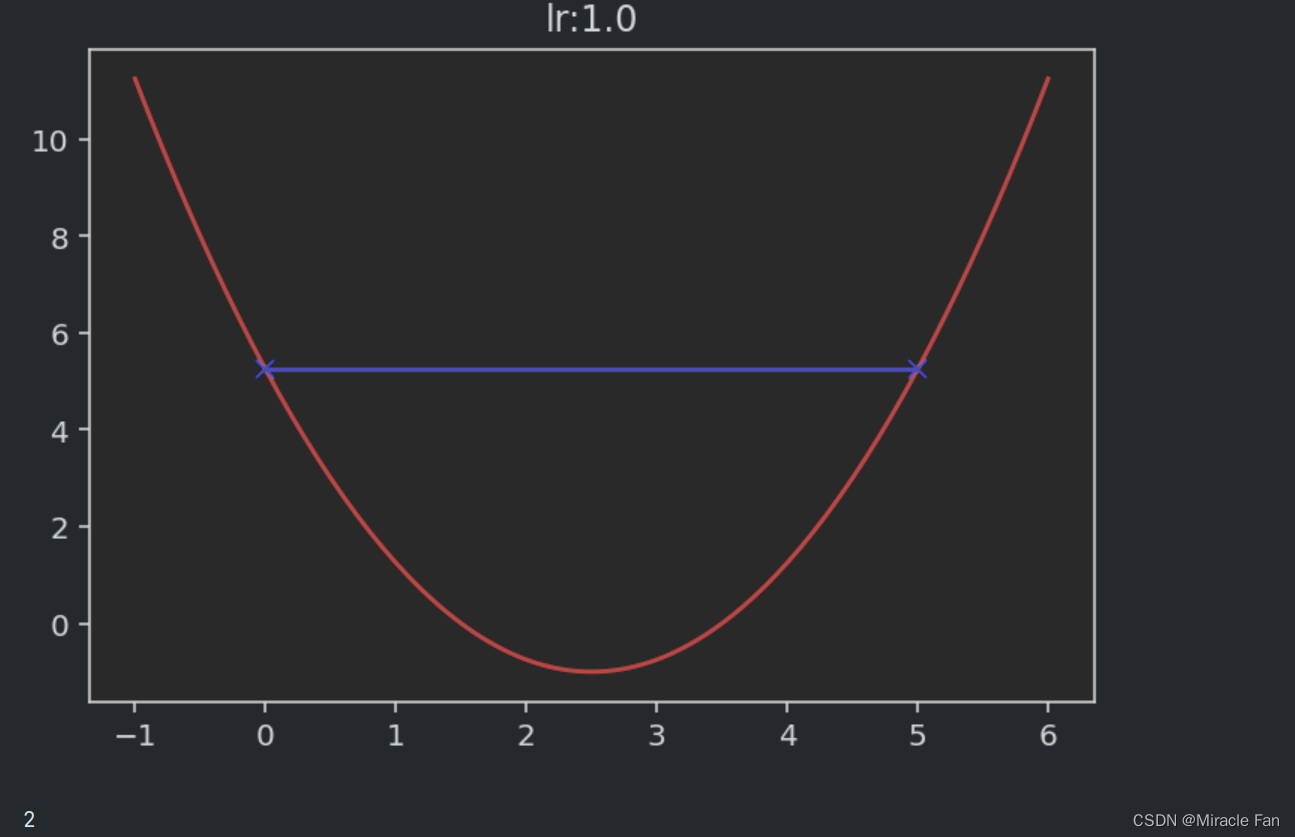
相关的取不同的学习率时,下降图如下所示。学习率一般在0~1之间,如下图当学习率为1时,已经达不到收敛状态,而当学习率大于1时,其会呈现一个发散的状态。

Logistic回归的损失函数
Logistic回归将线性回归融入后的表达式如下所示:
p = 1 1 + e − θ X p=\frac{1}{1+e^{-\theta X}} p=1+e−θX1
对于Logistic回归,一般采用的是对数损失函数,进行参数的计算。
c o s t = { − log ( p p r e d ) i f y = 1 − log ( 1 − p p r e d ) i f y = 0 cost=\left \{\begin{matrix} -\log^{(p_{pred})} \quad if &y=1\\ -\log^{(1-p_{pred})} \quad if &y=0 \end{matrix}\right. cost={ −log(ppred)if−log(1−ppred)ify=1y=0
稍作整理可以合成一个损失函数:
c o s t = − y log ( p p r e d ) − ( 1 − y ) log ( 1 − p p r e d ) cost=-y\log(p_{pred})-(1-y)\log({1-p_{pred}}) cost=−ylog(ppred)−(1−y)log(1−ppred)
import numpy as np
class LogisticRegression:
def __init__(self):
self.coef_ = None
self.intercept_ = None
self._theta = None
def _sigmoid(self, x):
y = 1.0 / (1.0 + np.exp(-x))
return y
def fit(self, x_train, y_train, eta=0.01, n_iters=1e4):
assert x_train.shape[0] == y_train.shape[0], '训练集和其标签长度样本数量需要一一致'
def J(theta, x, y):
p_pred = self._sigmoid(x.dot(theta))
try:
return -np.sum(y * np.log(p_pred) + (1 - y) * np.log(1 - p_pred)) / len(y)
except:
return float('inf')
def dJ(theta, x, y):
x = self._sigmoid(x.dot(theta))
return x.dot(x - y) / len(x)
# 模拟梯度下降
def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
theta = initial_theta
i_iter = 0
while i_iter < n_iters:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
i_iter += 1
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
return theta
X_b = np.hstack([np.ones((len(x_train), 1)), x_train])
initial_theta = np.zeros(X_b.shape[1]) # 列向量
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
self.intercept_ = self._theta[0] # 截距
self.coef_ = self._theta[1:] # 维度
return self
def predict_proba(self, X_predict):
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return self._sigmoid(X_b.dot(self._theta))
def predict(self, X_predict):
proba = self.predict_proba(X_predict)
return np.array(proba > 0.5, dtype='int')
边栏推荐
- One of the small practical projects - food alliance ordering system
- 简单谈谈Feign
- 【Go语言入门】一文搞懂Go语言的最新依赖管理:go mod的使用
- 单点登录 思维导图
- 服务器和客户端信息的获取
- 把 VS Code 当游戏机
- 深度学习通信领域相关经典论文、数据集整理分享
- Postgresql source code learning (34) - transaction log ⑩ - full page write mechanism
- Obtaining server and client information
- LeetCode:952. 按公因数计算最大组件大小【欧拉筛 + 并查集】
猜你喜欢
服务器和客户端信息的获取

Yu Mr Series 】 【 2022 July 022 - Go Go teaching course of container in the dictionary
![[PSQL] SQL基础教程读书笔记(Chapter1-4)](/img/76/d416f79b7f2c93c1c79a285c30d3e6.png)
[PSQL] SQL基础教程读书笔记(Chapter1-4)

小实战项目之——吃货联盟订餐系统
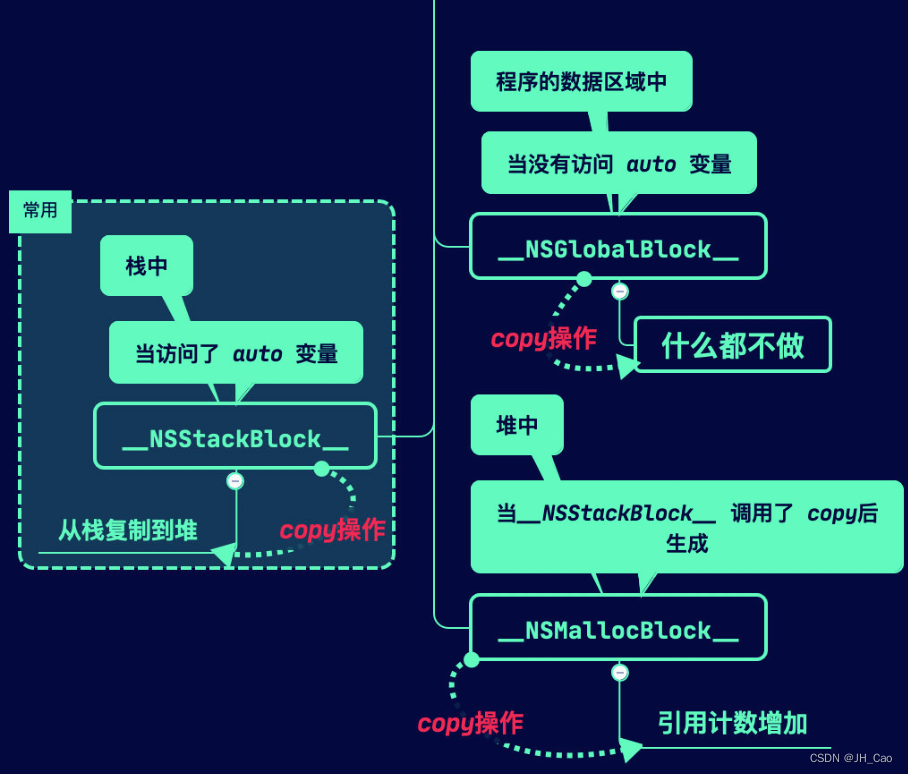
iOS大厂面试查漏补缺
Difficulty comparison between high concurrency and multithreading (easy to confuse)

Obtaining server and client information
【科普向】5G核心网架构和关键技术

SCI写作指南
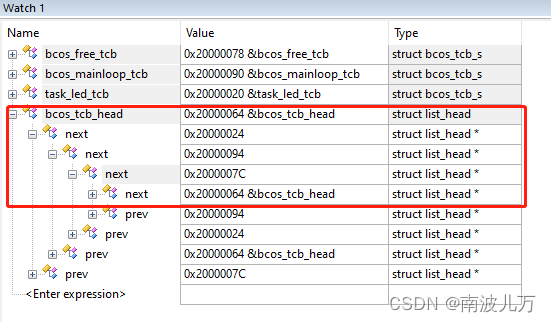
链表实现及任务调度
随机推荐
leetcode 406. Queue Reconstruction by Height
线程唤醒机制
shell之条件语句(test、if、case)
科普 | “大姨太”ETH 和 “小姨太”ETC的爱恨情仇
Kubernetes调度
360 push-360 push tool-360 batch push tool
One of the small practical projects - food alliance ordering system
LeetCode:952. 按公因数计算最大组件大小【欧拉筛 + 并查集】
2022.07.14_每日一题
基于交替迭代法的交直流混合系统潮流计算matlab程序iEEE9节点系统算例
【Go】Go 语言切片(Slice)
Zotero | Zotero translator插件更新 | 解决百度学术文献无法获取问题
多进程全局变量失效、变量共享问题
Titanic 预测问题
【Go语言刷题篇】Go完结篇函数、结构体、接口、错误入门学习
2022.07.18_每日一题
任务及任务切换
【并发编程】ReentrantLock的lock()方法源码分析
2022.07.18 _ a day
完美指南|如何使用 ODBC 进行无代理 Oracle 数据库监控?