当前位置:网站首页>熵-条件熵-联合熵-互信息-交叉熵
熵-条件熵-联合熵-互信息-交叉熵
2022-06-30 17:49:00 【古路】
熵-条件熵-联合熵-互信息-交叉熵
0.引言
属于信息论基本概念。
1.信息熵 Entropy (information theory)
信息量: x = l o g 2 N x = log_2N x=log2N, N N N 为等可能事件数量。例如,信息量为3,则原始等可能事件数为 2 3 = 8 2^3=8 23=8.



信号量是信息熵的一个特例:事件是等可能发生的。
- 假设一个硬币:正面出现的概率为 0.8, 反面出现的概率为 0.2
- 将其转换为等可能事件( N = 1 / p N = 1/p N=1/p):
- 正面–>想象为 1 / 0.8 = 1.25 1/0.8=1.25 1/0.8=1.25 个等可能事件中出现一次的概率
- 反面–>想象为 1 / 0.2 = 5 1/0.2=5 1/0.2=5 个等可能事件中出现一次的概率
- 则此时的信息量为: 直观的信息量应为 l o g 1.25 + l o g 5 log1.25 + log5 log1.25+log5,由于这两个等可能事件出现的概率也不同,所以此时真正的信息量为融入概率后的: 0.8 ∗ l o g 1.25 + 0.2 ∗ l o g 5 = 0.8 ∗ l o g 1 0.8 + 0.2 ∗ l o g 1 0.2 0.8*log1.25 + 0.2*log5 = 0.8*log\frac{1}{0.8} + 0.2*log\frac{1}{0.2} 0.8∗log1.25+0.2∗log5=0.8∗log0.81+0.2∗log0.21.
- 这就得出了著名的信息熵公式: Σ p i l o g 1 p i = − Σ p i l o g p i \Sigma{p_ilog\frac{1}{p_i}} = - \Sigma p_ilogp_i Σpilogpi1=−Σpilogpi
- H ( X ) = − ∑ i = 1 n p ( x i ) log p ( x i ) H(X)=-\sum_{i=1}^{n} p\left(x_{i}\right) \log p\left(x_{i}\right) H(X)=−∑i=1np(xi)logp(xi)
这篇文章中给出了定义:
定义:熵, 用来度量信息的不确定程度。
解释: 熵越大,信息量越大。不确定程度越低,熵越小,比如“明天太阳从东方升起”这句话的熵为0,因为这个句话没有带有任何信息,它描述的是一个确定无疑的事情。
例子也很直观:
例子:假设有随机变量X,用来表达明天天气的情况。X可能出现三种状态 1) 晴天2) 雨天 3)阴天 每种状态的出现概率均为 P(i) = 1/3,那么根据熵的公式: H ( X ) = − ∑ i = 1 n p ( x i ) log p ( x i ) H(X)=-\sum_{i=1}^{n} p\left(x_{i}\right) \log p\left(x_{i}\right) H(X)=−∑i=1np(xi)logp(xi)
可以计算得到:H(X) = - 1/3 * log(1/3) - 1/3 * log(1/3) + 1/3 * log(1/3) = log3 =0.47712
如果这三种状态出现的概率为(0.1, 0.1, 0.8):H(X) = -0.1 * log(0.1) *2 - 0.8 * log(0.8) = 0.277528
可以发现前面一种分布X的不确定程度很高(熵值很高),每种状态都很有可能。后面一种分布,X的不确定程度较低(熵值较低),第三种状态有很大概率会出现。
2.条件熵 Conditional entropy
定义:在一个条件下,随机变量的不确定性。
- 两个随机变量X,Y的分布,可以形成联合熵(Joint Entropy),用H(X, Y)表示。即: H ( X , Y ) = − Σ p ( x , y ) l o g ( x , y ) H(X, Y) = -Σp(x, y) log(x, y) H(X,Y)=−Σp(x,y)log(x,y)
- H ( X ∣ Y ) = H ( X , Y ) − H ( Y ) H(X|Y) = H(X, Y) - H(Y) H(X∣Y)=H(X,Y)−H(Y), 表示(X, Y)发生所包含的熵,减去Y单独发生包含的熵:在Y发生的前提下,X发生新带来的熵。
H ( X ∣ Y ) = H ( X , Y ) − H ( X ) = − ∑ x , y p ( x , y ) log p ( x , y ) + ∑ x p ( x ) log p ( x ) = − ∑ x , y p ( x , y ) log p ( x , y ) + ∑ x ( ∑ y p ( x , y ) ) log p ( x ) = − ∑ x , y p ( x , y ) log p ( x , y ) + ∑ x , y p ( x , y ) log p ( x ) = − ∑ x , y p ( x , y ) log p ( x , y ) p ( x ) = − ∑ x , y p ( x , y ) log p ( y ∣ x ) \begin{aligned} &H(X|Y) = H(X, Y)-H(X) \\ &=-\sum_{x, y} p(x, y) \log p(x, y)+\sum_{x} p(x) \log p(x) \\ &=-\sum_{x, y} p(x, y) \log p(x, y)+\sum_{x}\left(\sum_{y} p(x, y)\right) \log p(x) \\ &=-\sum_{x, y} p(x, y) \log p(x, y)+\sum_{x, y} p(x, y) \log p(x) \\ &=-\sum_{x, y} p(x, y) \log \frac{p(x, y)}{p(x)} \\ &=-\sum_{x, y} p(x, y) \log p(y \mid x) \end{aligned} H(X∣Y)=H(X,Y)−H(X)=−x,y∑p(x,y)logp(x,y)+x∑p(x)logp(x)=−x,y∑p(x,y)logp(x,y)+x∑(y∑p(x,y))logp(x)=−x,y∑p(x,y)logp(x,y)+x,y∑p(x,y)logp(x)=−x,y∑p(x,y)logp(x)p(x,y)=−x,y∑p(x,y)logp(y∣x)
3.联合熵 Joint Entropy
两个离散随机变量 X ,Y 的联合熵(以比特为单位)定义为:
H ( X , Y ) = − ∑ x ∈ X ∑ y ∈ Y P ( x , y ) log 2 [ P ( x , y ) ] {\displaystyle \mathrm {H} (X,Y)=-\sum _{x\in {\mathcal {X}}}\sum _{y\in {\mathcal {Y}}}P(x,y )\log _{2}[P(x,y)]} H(X,Y)=−x∈X∑y∈Y∑P(x,y)log2[P(x,y)]
对于两个以上的随机变量 X 1 , . . . , X n X_{1},...,X_{n} X1,...,Xn 扩展:
H ( X 1 , . . . , X n ) = − ∑ x 1 ∈ X 1 . . . ∑ x n ∈ X n P ( x 1 , . . . , x n ) log 2 [ P ( x 1 , . . . , x n ) ] {\displaystyle \mathrm {H} (X_{1},...,X_{n})=-\sum _{x_{1}\in {\mathcal {X}}_{1}}... \sum _{x_{n}\in {\mathcal {X}}_{n}}P(x_{1},...,x_{n})\log _{2}[P(x_{1 },...,x_{n})]} H(X1,...,Xn)=−x1∈X1∑...xn∈Xn∑P(x1,...,xn)log2[P(x1,...,xn)]
4.互信息 Mutual information
定义:指的是两个随机变量之间的相关程度。
理解:确定随机变量X的值后,另一个随机变量Y不确定性的削弱程度,因而互信息取值最小为0,意味着给定一个随机变量对确定一另一个随机变量没有关系,最大取值为随机变量的熵,意味着给定一个随机变量,能完全消除另一个随机变量的不确定性。这个概念和条件熵相对。
I ( X ; Y ) ≡ H ( X ) − H ( X ∣ Y ) ≡ H ( Y ) − H ( Y ∣ X ) ≡ H ( X ) + H ( Y ) − H ( X , Y ) ≡ H ( X , Y ) − H ( X ∣ Y ) − H ( Y ∣ X ) {\displaystyle {\begin{aligned}\operatorname {I} (X;Y)&{}\equiv \mathrm {H} (X)-\mathrm {H} (X\mid Y)\\&{}\equiv \mathrm {H} (Y)-\mathrm {H} (Y\mid X)\\&{}\equiv \mathrm {H} (X)+\mathrm {H} (Y)-\mathrm {H} (X,Y)\\&{}\equiv \mathrm {H} (X,Y)-\mathrm {H} (X\mid Y)-\mathrm {H} (Y\mid X)\end{aligned}}} I(X;Y)≡H(X)−H(X∣Y)≡H(Y)−H(Y∣X)≡H(X)+H(Y)−H(X,Y)≡H(X,Y)−H(X∣Y)−H(Y∣X)
I ( X ; Y ) = ∑ x ∈ X , y ∈ Y p ( X , Y ) ( x , y ) log p ( X , Y ) ( x , y ) p X ( x ) p Y ( y ) = ∑ x ∈ X , y ∈ Y p ( X , Y ) ( x , y ) log p ( X , Y ) ( x , y ) p X ( x ) − ∑ x ∈ X , y ∈ Y p ( X , Y ) ( x , y ) log p Y ( y ) = ∑ x ∈ X , y ∈ Y p X ( x ) p Y ∣ X = x ( y ) log p Y ∣ X = x ( y ) − ∑ x ∈ X , y ∈ Y p ( X , Y ) ( x , y ) log p Y ( y ) = ∑ x ∈ X p X ( x ) ( ∑ y ∈ Y p Y ∣ X = x ( y ) log p Y ∣ X = x ( y ) ) − ∑ y ∈ Y ( ∑ x ∈ X p ( X , Y ) ( x , y ) ) log p Y ( y ) = − ∑ x ∈ X p X ( x ) H ( Y ∣ X = x ) − ∑ y ∈ Y p Y ( y ) log p Y ( y ) = − H ( Y ∣ X ) + H ( Y ) = H ( Y ) − H ( Y ∣ X ) . {\displaystyle {\begin{aligned}\operatorname {I} (X;Y)&{}=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p_{(X,Y)}(x,y)\log {\frac {p_{(X,Y)}(x,y)}{p_{X}(x)p_{Y}(y)}}\\&{}=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p_{(X,Y)}(x,y)\log {\frac {p_{(X,Y)}(x,y)}{p_{X}(x)}}-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p_{(X,Y)}(x,y)\log p_{Y}(y)\\&{}=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p_{X}(x)p_{Y\mid X=x}(y)\log p_{Y\mid X=x}(y)-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p_{(X,Y)}(x,y)\log p_{Y}(y)\\&{}=\sum _{x\in {\mathcal {X}}}p_{X}(x)\left(\sum _{y\in {\mathcal {Y}}}p_{Y\mid X=x}(y)\log p_{Y\mid X=x}(y)\right)-\sum _{y\in {\mathcal {Y}}}\left(\sum _{x\in {\mathcal {X}}}p_{(X,Y)}(x,y)\right)\log p_{Y}(y)\\&{}=-\sum _{x\in {\mathcal {X}}}p_{X}(x)\mathrm {H} (Y\mid X=x)-\sum _{y\in {\mathcal {Y}}}p_{Y}(y)\log p_{Y}(y)\\&{}=-\mathrm {H} (Y\mid X)+\mathrm {H} (Y)\\&{}=\mathrm {H} (Y)-\mathrm {H} (Y\mid X).\\\end{aligned}}} I(X;Y)=x∈X,y∈Y∑p(X,Y)(x,y)logpX(x)pY(y)p(X,Y)(x,y)=x∈X,y∈Y∑p(X,Y)(x,y)logpX(x)p(X,Y)(x,y)−x∈X,y∈Y∑p(X,Y)(x,y)logpY(y)=x∈X,y∈Y∑pX(x)pY∣X=x(y)logpY∣X=x(y)−x∈X,y∈Y∑p(X,Y)(x,y)logpY(y)=x∈X∑pX(x)⎝⎛y∈Y∑pY∣X=x(y)logpY∣X=x(y)⎠⎞−y∈Y∑(x∈X∑p(X,Y)(x,y))logpY(y)=−x∈X∑pX(x)H(Y∣X=x)−y∈Y∑pY(y)logpY(y)=−H(Y∣X)+H(Y)=H(Y)−H(Y∣X).
- 两个随机变量 X , Y X,Y X,Y 的互信息,定义为 X , Y X,Y X,Y 的联合分布和独立分布乘积的相对熵。
- I ( X , Y ) = D ( P ( X , Y ) ∣ ∣ P ( X ) P ( Y ) ) I(X,Y)=D(P(X,Y) || P(X)P(Y)) I(X,Y)=D(P(X,Y)∣∣P(X)P(Y)) , I ( X , Y ) = ∑ x , y p ( x , y ) log p ( x , y ) p ( x ) p ( y ) I(X, Y)=\sum_{x, y} p(x, y) \log \frac{p(x, y)}{p(x) p(y)} I(X,Y)=∑x,yp(x,y)logp(x)p(y)p(x,y)
互信息和信息增益实际是同一个值。信息增益 = 熵 – 条件熵, g ( D , A ) = H ( D ) – H ( D ∣ A ) g(D,A)=H(D) – H(D|A) g(D,A)=H(D)–H(D∣A)

5.相对熵
相对熵,又称互熵,交叉熵,鉴别信息,Kullback熵,Kullback-Leible散度等.
设 p ( x ) 、 q ( x ) p(x)、q(x) p(x)、q(x) 是 X X X 中取值的两个概率分布,则 p p p 对 q q q 的相对熵是
D KL ( P ∥ Q ) = ∑ x ∈ X P ( x ) log ( P ( x ) Q ( x ) ) = − ∑ x ∈ X P ( x ) log ( Q ( x ) P ( x ) ) {\displaystyle D_{\text{KL}}(P\parallel Q)=\sum _{x\in {\mathcal {X}}}P(x)\log \left({\frac {P(x)}{Q(x)}}\right)=-\sum _{x\in {\mathcal {X}}}P(x)\log \left({\frac {Q(x)}{P(x)}}\right)} DKL(P∥Q)=x∈X∑P(x)log(Q(x)P(x))=−x∈X∑P(x)log(P(x)Q(x))
说明:
- 相对熵可以度量两个随机变量的“距离”
- 一般的, D ( p ∣ ∣ q ) ≠ D ( q ∣ ∣ p ) D(p||q) ≠D(q||p) D(p∣∣q)=D(q∣∣p)
边栏推荐
- 浏览器窗口切换激活事件 visibilitychange
- Electronic components bidding and purchasing Mall: optimize traditional purchasing business and speed up enterprise digital upgrading
- Opencv data type code table dtype
- PC wechat multi open
- [community star selection] the 23rd issue of the July revision plan | bit by bit creation, converging into a tower! Huawei freebuses 4E and other cool gifts
- mysql下载和安装详细教程
- The cloud native landing practice of using rainbow for Tuowei information
- Small program container technology to promote the operation efficiency of the park
- 20220528【聊聊假芯片】贪便宜往往吃大亏,盘点下那些假的内存卡和固态硬盘
- openGauss数据库源码解析系列文章—— 密态等值查询技术详解(上)
猜你喜欢

dtd建模

How to seamlessly transition from traditional microservice framework to service grid ASM

正则表达式(正则匹配)

What if icloud photos cannot be uploaded or synchronized?

【TiDB】TiCDC canal_ Practical application of JSON

Digital intelligent supplier management system solution for coal industry: data driven, supplier intelligent platform helps enterprises reduce costs and increase efficiency
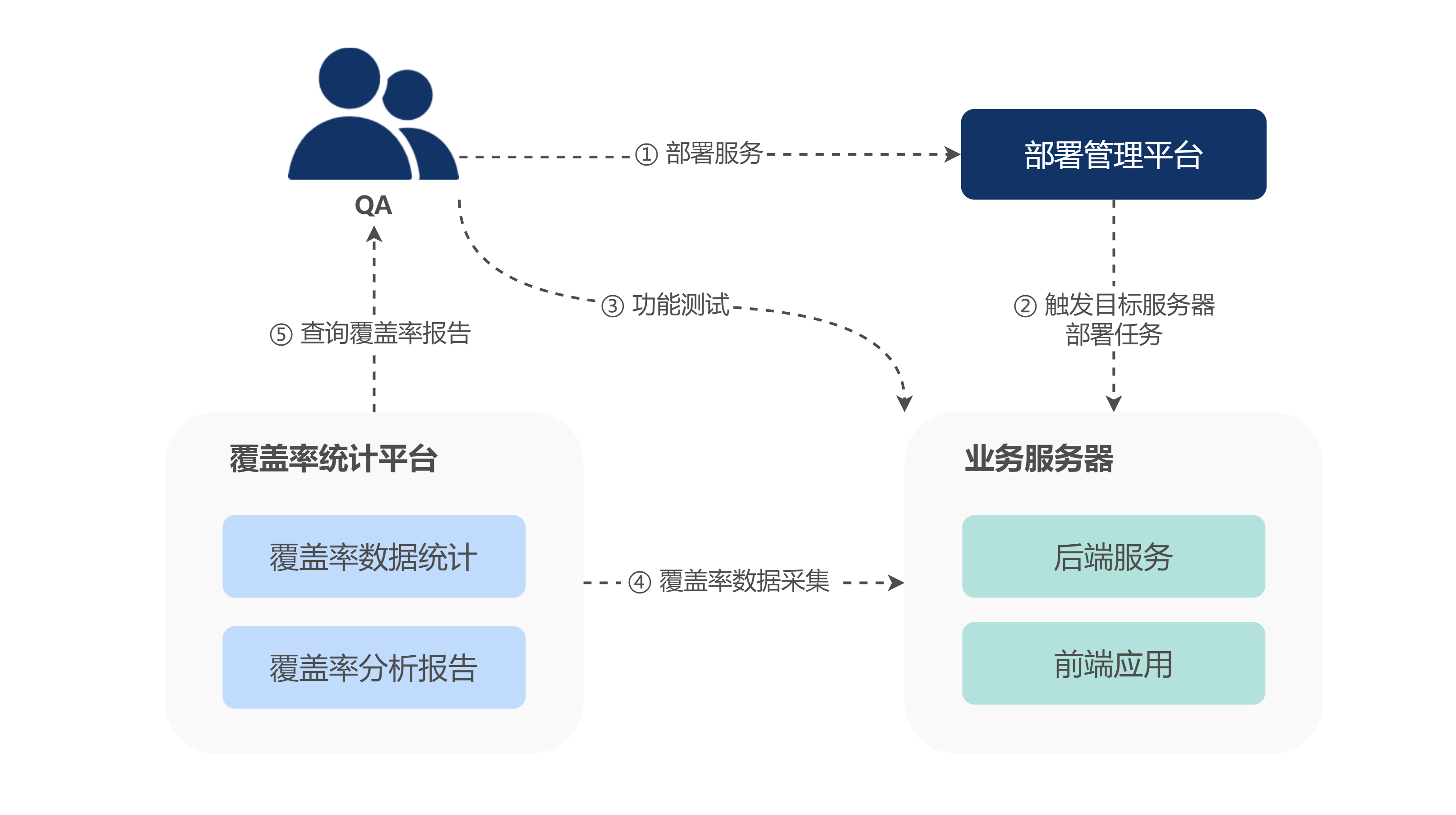
Construction and practice of full stack code test coverage and use case discovery system

Troubleshooting MySQL for update deadlock
The cloud native landing practice of using rainbow for Tuowei information

一点比较有意思的模块
随机推荐
《客从何处来》
NFT technology for gamefi chain game system development
AI chief architect 10-aica-lanxiang, propeller frame design and core technology
法国A+ 法国VOC标签最高环保级别
What if the apple watch fails to power on? Apple watch can not boot solution!
Cobbler轻松上手
冰河老师的书
AI首席架构师10-AICA-蓝翔 《飞桨框架设计与核心技术》
go之web框架 iris
Neon optimization 2: arm optimization high frequency Instruction Summary
「杂谈」如何改善数据分析工作中的三大被动局面
slice
屏幕显示技术进化史
Regular expressions (regular matching)
php利用队列解决迷宫问题
C WinForm program interface optimization example
亲测flutter打包apk后大小,比较满意
服务器之间传文件夹,文件夹内容为空
电子元器件招标采购商城:优化传统采购业务,提速企业数字化升级
4个技巧告诉你,如何使用SMS促进业务销售?