Miller_Rabin 米勒拉宾概率筛【模板】

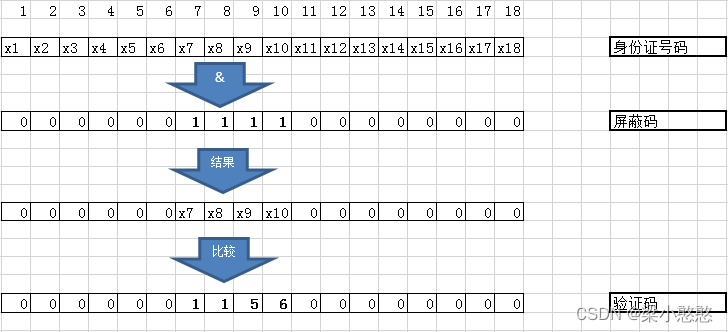
Miller_Rabin筛法是一种正确率极高，复杂度优秀的概率筛法，将质数分为2和奇质数，对于奇质数n，将n-1其分解为 2^p  +  m ，然后，取若干[1,n-1]的随机数a,本模板取了20次，每次判断是否有

a^m 三 1（mod n) 或者  是否有 [0,p-1]的j,满足 a^(2jm) 三 n-1 (mod n)   

满足二者之一表示本次判断成功，20次中有一次失败就表明不是素数，20次都成功，那么可以说是一个素数。

验证正确性如下，取2-1e6全部数字，进行正确性判断，正确个数1e6-1，全部正确

甚至可以将判断次数缩小至5，也能保证完全正确

 

# include<iostream>
# include<iomanip>
# include<math.h>

using namespace std;
typedef long long int ll;


ll random(ll n)  //生成[0,n]范围内随机数
{
    return rand()%(n-1);

}
ll quick_mul(ll a, ll b, ll mod)
{

    ll ans=0;

    while(b)
    {
        if(b&1)
            ans=(ans+a)%mod;

        a=(a+a)%mod;
        b>>=1;

    }
    return ans;
}
ll quick_pow(ll base,ll pow, ll mod)
{
    ll ans=1;

    while(pow)
    {
        if(pow&1)
            ans=ans*base%mod;
        pow>>=1;

        base=base*base%mod;
    }
    return ans;

}
bool witness(ll a, ll n)
{
    ll temp=n-1;
    int j=0;
    while(temp%2==0)
    {
        temp/=2;
        j++;
    }
    ll x=quick_pow(a,temp,n);

    if(x==1||x==n-1)
        return 1;

    while(j--)
    {
        x=quick_mul(x,x,n);

        if(x==n-1)
            return 1;

    }
    return 0;
}

bool miller_rabin(ll n)
{

    if(n==2)
        return 1;
    if(n<2||n%2==0)
        return 0;

    for(int i=1; i<=20; i++)
    {
        ll a=random(n)+1;

    //    cout<<a<<endl;

        if(!witness(a,n))
            return 0;
    }
    return 1;

}

int prime[1000000+10];
bool not_prime[1000000+10];
int tot;

void init()
{
    for(int i=2; i<=1000000; i++)
    {
        if(!not_prime[i])
        {
            tot++;

            prime[tot]=i;

        }

        for(int j=1; j<=tot&&prime[j]*i<=1000000; j++)
        {
            not_prime[i*prime[j]]=1;

            if(i%prime[j]==0)
            {
                break;

            }
        }
    }
}
int main ()
{

    init();

    ll n;
    int cnt=0;

     for(n=2;n<=1000000;n++)
     {
         if(miller_rabin(n)!=(!not_prime[n]))
         {
             cout<<"***";
         }
         else
            cnt++;
     }

     cout<<cnt<<endl;
    return 0;

}