Introduction to Cosine Distance

概述： 在机器学习领域中,通常将特征表示为向量的形式,所以在分析两个特征向量之间的相似性时,Commonly used cosine similarity representation.

For example, two articles are vectorized,Cosine distance can avoid large distances due to different lengths of articles,The cosine distance only considers the angle between the vectors generated by the two articles.

余弦相似度的取值范围是[-1,1],相同两个向量的之间的相似度为1.

余弦距离的取值范围是[0,2].

The definition formula of cosine similarity is $cos(A,B)=\frac{A\cdot B}{{\Vert A\Vert }_2{\Vert B\Vert }_2}$

归一化后：${\Vert A\Vert }_2=1,{\Vert B\Vert }_2=1,{\Vert A\Vert }_2{\Vert B\Vert }_2=1$

余弦距离：$dist(A,B)=1-cos(A,B)=\frac{{\Vert A\Vert }_2{\Vert B\Vert }_2-A\cdot B}{{\Vert A\Vert }_2{\Vert B\Vert }_2}$,distance is greater than0

欧式距离：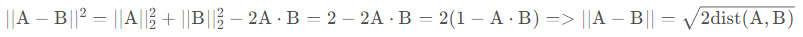

It can be seen from the formula that after normalization,There is a monotonic relationship between Euclidean distance and cosine distance.At this time, the value range of both distances is [0,2].

Euclidean distance vs cosine distance：

• 1.欧式距离的数值受到维度的影响,余弦相似度在高维的情况下也依然保持低维完全相同时相似度为1等性质.

• 2.欧式距离体现的是距离上的绝对差异,The cosine distance reflects the relative difference in direction.