当前位置:网站首页>PreFixSum前缀和
PreFixSum前缀和
2022-08-03 18:26:00 【兴趣使然的小小】
参考链接:
【宫水三叶】啥是前缀和呀?图解前缀和(含模板) - 区域和检索 - 数组不可变 - 力扣(LeetCode)
引入:
如果要得到「区间和」,能想到最简单的方法就是遍历所求区间,循环相加即可。如果这种需求有很多,此时,时间复杂度为 O(n2)
基于上面描述的场景,我们完全可以使用「前缀和」优化,前缀和数组中每个元素的值为区间[0..i]的元素和
注意:前缀和适用于不变数组;对于变化的数组,可以使用「线段树」
原理:
一维前缀和:
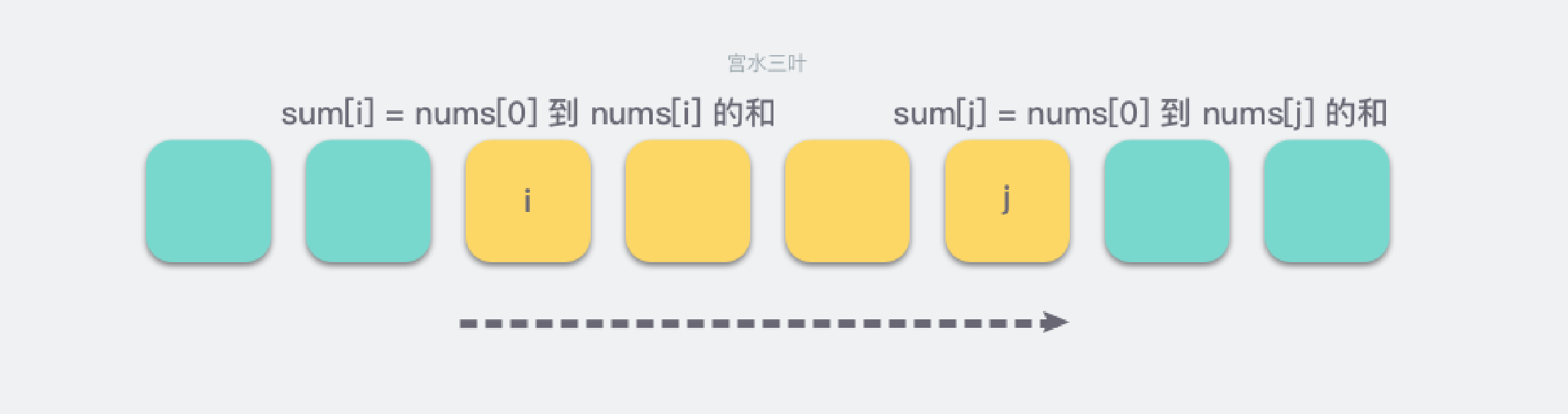
前缀和的作用就是为了帮助我们快速求某一段的和,是「差分」的逆运算。
前缀和数组 sum 的每一位记录的是当前位置距离起点位置,这连续一段的和区间和。
因此当我们要求特定的一段 [i,j] 的区域和的时候,可以直接利用前缀和数组快速求解:ans = sum[j] - sum[i - 1]。
二维前缀和:
「二维前缀和」解决的是二维矩阵中的矩形区域求和问题。
二维前缀和数组中的每一个格子记录的是「以当前位置为区域的右下角(区域左上角恒定为原数组的左上角)的区域和」
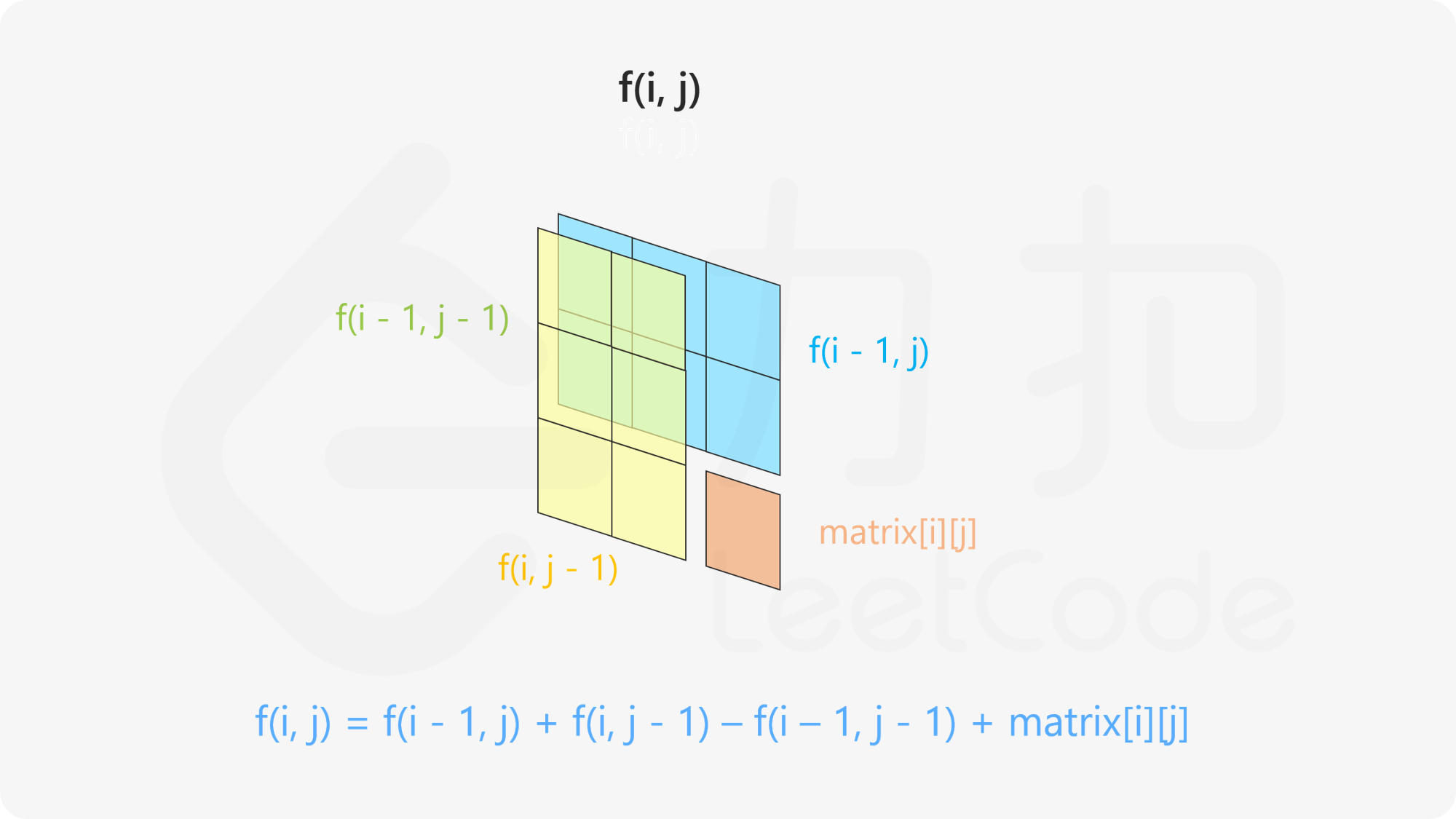
如果觉得不清晰,请将将 f[i][j] 理解成是以 (i, j) 为右下角,(0, 0) 为左上角的区域和。
二维前缀和数组初始化:
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
记作12 + 21 - 11 + 11
因此当我们要求 (x1, y1) 作为左上角,(x2, y2) 作为右下角 的区域和的时候,可以直接利用前缀和数组快速求解:
sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1]
记作 22 - 12 - 21 + 11,然后 不减,减第一位,减第二位,减两位
也可以记作22 - 12(x - 1) - 21(y - 1) + 11(x y 都 - 1)
模板:
一维前缀和模板:
// 预处理前缀和数组
{
sum = new int[n + 1];
for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + nums[i - 1];
}
// 计算 [i, j] 结果
{
i++; j++;
ans = sum[j] - sum[i - 1];
}
二维前缀和模板:
// 预处理前缀和数组
{
sum = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 当前格子(和) = 上方的格子(和) + 左边的格子(和) - 左上角的格子(和) + 当前格子(值)【和是指对应的前缀和,值是指原数组中的值】
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
}
// 首先我们要令左上角为 (x1, y1) 右下角为 (x2, y2)
// 计算 (x1, y1, x2, y2) 的结果
{
// 前缀和是从 1 开始,原数组是从 0 开始,上来先将原数组坐标全部 +1,转换为前缀和坐标
x1++; y1++; x2++; y2++;
// 记作 22 - 12 - 21 + 11,然后 不减,减第一位,减第二位,减两位
// 也可以记作 22 - 12(x - 1) - 21(y - 1) + 11(x y 都 - 1)
ans = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
}
总结:
总结
最后我们看看「前缀和」与其他知识点的联系。
为啥「前缀和」能大幅度的降低区间求和的复杂度?其实本质是利用数学进行求值:某一段的区间和 = 起点到区间右端点的和(含右端点)- 起点到区间左端点的和(不含左端点)
而求解前缀和数组的过程,则是基于动态规划思想:由于前缀和的每一位都是求「当前位置到起点位置区间的和」。因此当求解某一位的前缀和时,需要「前一位置的前缀和」和「当前位置的原数组值」(而与前一位置的前缀和是如何计算出来无关)。其过程类似于 dp 入门题 509. 斐波那契数 - 力扣(LeetCode)的求解过程。
题目实战:
区域和检索 - 数组不可变
题目详情可见 区域和检索 - 数组不可变
建议:preSum[]整体向后偏移一位,简便处理
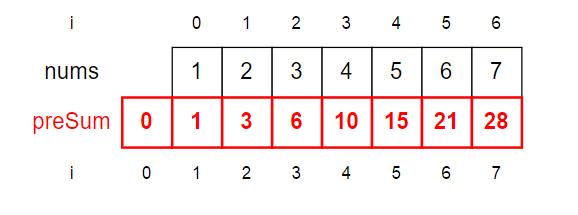
如果求区间[2,4]的和,只需计算preSum[4 + 1] - preSum[2]即可
下面给出详细代码:
class NumArray {
int[] sum;
public NumArray(int[] nums) {
int n = nums.length;
// 前缀和数组下标从 1 开始,因此设定长度为 n + 1(模板部分)
sum = new int[n + 1];
// 预处理除前缀和数组(模板部分)
for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + nums[i - 1];
}
public int sumRange(int i, int j) {
// 求某一段区域和 [i, j] 的模板是 sum[j] - sum[i - 1](模板部分)
// 但由于我们源数组下标从 0 开始,因此要在模板的基础上进行 + 1
i++; j++;
return sum[j] - sum[i - 1];
}
}
二维区域和检索 - 矩阵不可变
题目详情可见 二维区域和检索 - 矩阵不可变
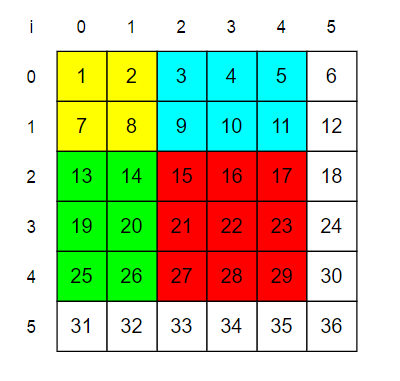
如果求红色区间的和,只需求preSum[4,4] - preSum[1,4] - preSum[4,1] + preSum[1,1]即可
preSum[4,4]:黄 + 蓝 + 绿 + 红preSum[1,4]:黄 + 蓝preSum[4,1]:黄 + 绿preSum[1,1]:黄
下面给出详细代码:
class NumMatrix {
private int[][] preSum;
public NumMatrix(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
preSum = new int[m + 1][n + 1];
for (int i = 1; i < m + 1; i++) {
for (int j = 1; j < n + 1; j++) {
preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i - 1][j - 1];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return preSum[row2 + 1][col2 + 1] - preSum[row1][col2 + 1] - preSum[row2 + 1][col1] + preSum[row1][col1];
}
}
和为 K 的子数组
题目详情可见 和为 K 的子数组
正常的思路:
//前缀和
class Solution {
int[] preSum;
int count = 0;
public int subarraySum(int[] nums, int k) {
preSum = new int[nums.length + 1];
for (int i = 1; i <= nums.length; i++) {
preSum[i] = preSum[i - 1] + nums[i - 1];//正常初始化数组
}
for (int left = 1; left <= nums.length; left++) {
//通过遍历区间和
for (int right = left; right <= nums.length; right++) {
//遍历区间和[left,right], 注意下标偏移.
if (preSum[right] - preSum[left - 1] == k) {
count++;
}
}
}
return count;
}
}
前缀和+哈希表优化版本:
优化思路:
由于只关心次数,不关心具体的解,我们可以使用哈希表加速运算;
由于保存了之前相同前缀和的个数,计算区间总数的时候不是一个一个地加,时间复杂度降到了 O(N)O(N)。
这个思路不是很容易想到,需要多做一些类似的问题慢慢培养感觉。同类问题有:
「力扣」第 1 题:两数之和;
「力扣」第 1248 题: 统计「优美子数组」;
「力扣」第 454 题:四数相加 II。
解释一开始preSumFreq.put(0, 1);的意义
想一想算法的意思:计算完包括了当前数前缀和以后,我们去查一查在当前数之前,有多少个前缀和等于 preSum - k 呢?
这是因为满足 preSum - (preSum - k) == k 的区间的个数是我们所关心的。对于一开始的情况,下标 0 之前没有元素,可以认为前缀和为 0,个数为 1 个,因此 preSumFreq.put(0, 1);,这一点是必要且合理的。
具体的例子是:nums = [3,…], k = 3,和 nums = [1, 1, 1,…], k = 3。
借鉴「两数和」的思路,利用HashMap
//前缀和+哈希表优化
class Solution {
// key:前缀和,value:key 对应的前缀和的个数
Map<Integer, Integer> preSumFreq = new HashMap<>();
public int subarraySum(int[] nums, int k) {
preSumFreq.put(0, 1);// 对于下标为 0 的元素,前缀和为 0,个数为 1
int preSum = 0;//当前前缀和
int count = 0;
for (int num : nums) {
preSum += num;//维护前缀和.
if (preSumFreq.containsKey(preSum - k)) {
//满足 preSum - (preSum - k) == k 其实就是preSum(当前)-preSum(以前) == k
count += preSumFreq.get(preSum-k);//注意这里
}
//维护preSumFreq
preSumFreq.put(preSum, preSumFreq.getOrDefault(preSum, 0) + 1);
}
return count;
}
}
公交站间的距离
//前缀和
class Solution {
public int distanceBetweenBusStops(int[] distance, int start, int destination) {
//虽说是个环形,但是依旧可以用前缀和来做。
int[] preSum = new int[distance.length + 1];
int allSum = 0;
for (int i = 1; i <= distance.length; i++) {
preSum[i] = preSum[i-1] + distance[i-1];
allSum += distance[i-1];
}
int ans = Math.abs(preSum[destination] - preSum[start]);//保证一定时大的减小的。
return Math.min(ans,allSum-ans);//取最小值
}
}
边栏推荐
猜你喜欢
随机推荐
开篇-开启全新的.NET现代应用开发体验
Postgresql 备份大小情况!
你想知道的 Watch App 开发
OSError: [WinError 123] 文件名、目录名或卷标语法不正确
ASA归因:如何评估关键词的投放价值
智能合约安全——delegatecall (2)
PHP基础笔记-NO.2
Uniswap或将开启“费用开关”,UNI持有者可享受分红
MySQL如何 drop 大表
阿里资深架构师钟华曰:中台战略思想与架构实战;含内部实施手册
ImportError: /lib/libgdal.so.26: undefined symbol: sqlite3_column_table_name
openresty 高可用部署
Discuz新闻资讯GBK模板
快手通过国际权威信息安全和隐私保护认证,安全能力达到国际领先水平
Execution plan of mysql
MySQL 啥时候用表锁,啥时候用行锁?这些你都应该知道吧
CodeTON Round 2 (Div. 1 + Div. 2, Rated, Prizes!) A-E
EasyNTS上云网关断电重启后设备离线是什么原因?
【Deliberately practice the view of the back tube】deliberately practice
技术开发人员常用的安全浏览器