当前位置:网站首页>注意力机制的详细理解
注意力机制的详细理解
2022-08-03 17:40:00 【如意的小家】
一、线性Attention的探索:Attention必须有个Softmax吗?
前几天笔者读到了论文 Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention [1] ,了解到了线性化 Attention (Linear Attention)这个探索点,继而阅读了一些相关文献,有一些不错的收获,最后将自己对线性化 Attention 的理解汇总在此文中.
Attention
相关解读可以参考笔者的一文读懂「Attention is All You Need」| 附代码实现,以及它的一些改进工作也可以参考突破瓶颈,打造更强大的 Transformer [3]、Google 新作 Synthesizer:我们还不够了解自注意力,这里就不多深入介绍了。
1.1 摘掉Softmax
读者也许想不到,制约 Attention 性能的关键因素,其实是定义里边的 Softmax!事实上,简单地推导一下就可以得到这个结论。 注:关于矩阵乘法算法复杂度的计算
注:关于矩阵乘法算法复杂度的计算
1).矩阵乘法
对于矩阵A(n×m),B(m×n), 这里A(n×m)表示A是n行乘m列的矩阵。
如果A×B,那么复杂度为O(n×m×n),即O(n^2×m) 。进一步思考,为什么呢,直接代码解释:
for(i=0;i<n;i++){
//A矩阵中的n
for(j=0;j<m;j++){
//A矩阵中的m 或者B矩阵中的m ,一样的
for(k=0;k<n;k++){
//B矩阵中的n
C[i][j]= C[i][j]+A[i][k]*B[k][j];
}
}
}
一个for循环是O(n),这里是三个for循环,所以为O(n×m×n)。(ps:个人感觉还是看代码比较好理解,后面三个矩阵乘法时,就会更加体会到)
对于矩阵A(m×n),B(n×m)和C(m×n), 这里A(m×n)表示A是m行乘n列的矩阵。(PS:这里记号和前面不同,主要方便和知乎截图符号一致)
- A×B,那么复杂度为O(m×n×m),即O(m^2×n) 。
- D(m×m)=A×B运算完后在和C运算。
- D×C,那么复杂度为O(m×m×n),即O(m^2×n) 。

为了方面理解,笔者直接上代码,这样清楚一点。
int A(m*n),
int B(n*m)
int C(m*n)
int D(m*m)
int E(m*n)
//先计算D=A*B
for(i=0;i<m;i++){
//A矩阵中的m
for(j=0;j<n;j++){
//A矩阵中的n 或者B矩阵中的n ,一样的
for(k=0;k<m;k++){
//B矩阵中的m
D[i][j]= D[i][j]+A[i][k]*B[k][j];
}
}
}
//在计算E=D*C
for(i=0;i<m;i++){
//D矩阵中的m
for(j=0;j<m;j++){
//D矩阵中的m 或者C矩阵中的m ,一样的
for(k=0;k<n;k++){
//C矩阵中的n
E[i][j]= E[i][j]+A[i][k]*B[k][j];
}
}
}

边栏推荐
猜你喜欢

论文解读(JKnet)《Representation Learning on Graphs with Jumping Knowledge Networks》
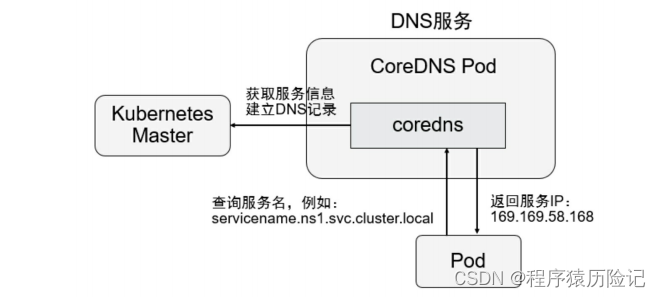
003_Kubernetes核心技术

leetcode-每日一题899. 有序队列(思维题)
我们为何看好投资 DAO?
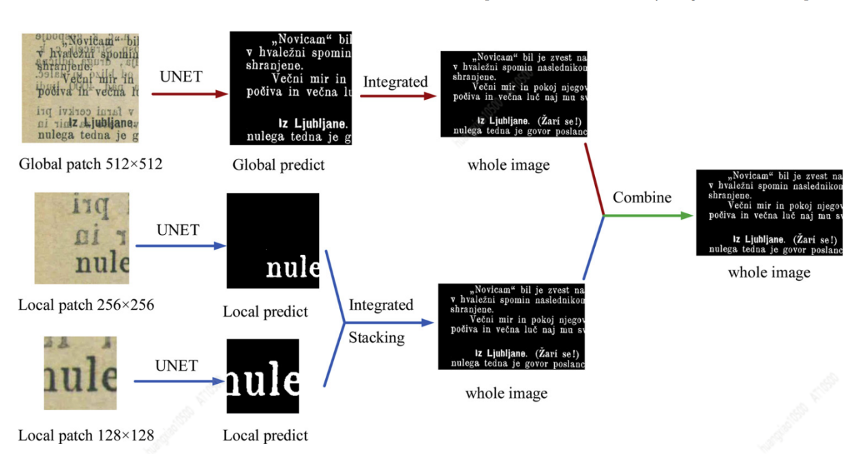
ICDAR competition technology sharing

分享 14 个你必须知道的 JS 函数

图像质量指标:PSNR、SSIM、MSE

并查集模板及思想

A complete detailed tutorial on building intranet penetration ngrok (with pictures and truth)

“vite”和“vite预览”有什么区别?
随机推荐
什么是鉴权?一篇文章带你了解postman的多种方式
【JS】利用JS给删除按钮添加提示框
405. Convert a Number to Hexadecimal
高效的组织信息共享知识库是一种宝贵的资源
九种方法!教你如何读取resources目录下的文件路径
【技术白皮书】第二章:OCR智能文字识别回顾——自然语言文本发展历程
【mysql】SIGN(x)函数
并发高的情况下,试试用ThreadLocalRandom来生成随机数
CC2530_ZigBee+HUAWEI CLOUD IOT: Design your own cold chain acquisition system
一些嵌入式软件设计经验
被误解的 MVC 和被神化的 MVVM(一)
JS 字符串转 GBK 编码超精简实现
uniapp 去掉默认导航栏
企业如何选择低代码开发平台
mysql之的执行计划
401. Binary Watch
vant自动上传图片/文件
通用型安全监测数据管理系统
Win11系统的显卡驱动安装的详细方法步骤
CAD如何自定义快捷键