当前位置:网站首页>使用Matlab实现:Jacobi、Gauss-Seidel迭代
使用Matlab实现:Jacobi、Gauss-Seidel迭代
2022-07-02 06:25:00 【霏霏小雨】
使用Matlab实现:Jacobi、Gauss-Seidel迭代
例题
方程组 { 5 x 1 + 2 x 2 + x 3 = − 12 − x 1 + 4 x 2 + 2 x 3 = 20 2 x 1 − 3 x 2 + 10 x 3 = 3 \begin{cases} 5x_1 + 2x_2 + x_3 = -12\\ -x_1 + 4x_2 + 2x_3 = 20\\ 2x_1 - 3x_2 + 10x_3 = 3\\ \end{cases} ⎩⎪⎨⎪⎧5x1+2x2+x3=−12−x1+4x2+2x3=202x1−3x2+10x3=3 求解,当 m a x ∣ x i ( k + 1 ) − x i ( k ) ∣ ≤ 1 0 − 5 max|x_i^{(k + 1)} - x_i^{(k)}| \leq 10^{-5} max∣xi(k+1)−xi(k)∣≤10−5 时候迭代终止。
以下解答过程,上标表示迭代次数,下标表示序号。
Jacobi迭代
定义变量:
D = d i a g ( a 11 , a 22 , . . . , a n n ) , L = [ 0 − a 21 0 . . . − a i 1 . . . − a i , i − 1 0 . . . − a n 1 . . . − a n , i − 1 . . . − a n , n − 1 0 ] , U = [ 0 − a 12 . . . − a 1 , i . . . − a 1 , n . . . 0 − a i − 1 , i . . . − a i − 1 , n . . . 0 − a n − 1 , n . . . 0 ] D = diag(a_{11}, a_{22}, ..., a_{nn}),\\ L = \left[\begin{array}{cccccc} 0\\ -a_{21} & 0\\ ...\\ -a_{i1} & ... & -a_{i,i-1} & 0\\ ...\\ -a_{n1} & ... & -a_{n,i-1} & ... & -a_{n,n-1} & 0\\ \end{array}\right],\\ U = \left[\begin{array}{cccccc} 0 &-a_{12} & ... & -a_{1,i} & ... & -a_{1,n}\\ ...\\ & & 0 & -a_{i-1,i} & ... & -a_{i-1,n}\\ ...\\ & & & & 0 & -a_{n-1,n}\\ ...\\ & & & & & 0\\ \end{array}\right] D=diag(a11,a22,...,ann),L=⎣⎢⎢⎢⎢⎢⎢⎡0−a21...−ai1...−an10......−ai,i−1−an,i−10...−an,n−10⎦⎥⎥⎥⎥⎥⎥⎤,U=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0.........−a12...0−a1,i−ai−1,i......0−a1,n−ai−1,n−an−1,n0⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
其矩阵迭代形式为:
x ( k + 1 ) = B J ⋅ x ( k ) + f J B J = D − 1 ⋅ ( L + U ) , f J = D − 1 ⋅ b x^{(k+1)} = B_J \cdot x^{(k)} + f_J\\ B_J = D^{-1} \cdot (L + U), \quad f_J = D^{-1} \cdot b x(k+1)=BJ⋅x(k)+fJBJ=D−1⋅(L+U),fJ=D−1⋅b。
写出分量形式:
{ x 1 ( k + 1 ) = 1 5 ( − 12 − 2 x 2 ( k ) − x 3 ( k ) ) x 2 ( k + 1 ) = 1 4 ( 20 + x 1 ( k ) − 2 x 3 ( k ) ) x 3 ( k + 1 ) = 1 10 ( 3 − 2 x 1 ( k ) + 3 x 2 ( k ) ) \begin{cases} x_1^{(k + 1)} = \frac15 (-12 - 2 x_2^{(k)} - x_3^{(k)} )\\ x_2^{(k + 1)} = \frac14 (20 + x_1^{(k)} - 2x_3^{(k)} )\\ x_3^{(k + 1)} = \frac1{10} (3 - 2 x_1^{(k)} + 3x_2^{(k)} )\\ \end{cases} ⎩⎪⎨⎪⎧x1(k+1)=51(−12−2x2(k)−x3(k))x2(k+1)=41(20+x1(k)−2x3(k))x3(k+1)=101(3−2x1(k)+3x2(k))
写成矩阵形式:
[ x 1 ( k + 1 ) x 2 ( k + 1 ) x 3 ( k + 1 ) ] = [ 0 − 0.4 − 0.2 0.25 0 − 0.5 − 0.2 0.3 0 ] ⋅ [ x 1 ( k ) x 2 ( k ) x 3 ( k ) ] + [ − 2.4 5 0.3 ] \left[\begin{array}{c} x_1^{(k + 1)}\\ x_2^{(k + 1)}\\ x_3^{(k + 1)}\\ \end{array}\right] = \left[\begin{array}{cccc} 0 & -0.4 & -0.2\\ 0.25 & 0 & -0.5\\ -0.2 & 0.3 & 0\\ \end{array}\right] \cdot \left[\begin{array}{c} x_1^{(k)}\\ x_2^{(k)}\\ x_3^{(k)}\\ \end{array}\right] + \left[\begin{array}{c} -2.4\\ 5\\ 0.3\\ \end{array}\right] ⎣⎢⎡x1(k+1)x2(k+1)x3(k+1)⎦⎥⎤=⎣⎡00.25−0.2−0.400.3−0.2−0.50⎦⎤⋅⎣⎢⎡x1(k)x2(k)x3(k)⎦⎥⎤+⎣⎡−2.450.3⎦⎤
取初始向量: x 0 = ( 0 , 0 , 0 ) T x^0 = (0, 0, 0)^T x0=(0,0,0)T,依次按照上式进行迭代。使用Matlab进行编程求解。
a=[0,-0.4,-0.2;0.25,0,-0.5;-0.2,0.3,0];
b = [-2.4;5;0.3];
x = [0;0;0];
xx = a * x + b;
i = 0;
while norm(x - xx, inf) >= 1e-5
x = xx;
xx = a * x + b;
i = i +1;
end
以上代码,最终 x = x i , x x = x ( i + 1 ) x = x^{i}, xx = x^{(i + 1)} x=xi,xx=x(i+1) ,最终迭代次数位 i + 1 i + 1 i+1 次,如果你需要看到更长的小数位置,可以使用以下Matlab代码,表示使用15位浮点或定点数。
format long g
运行结果为: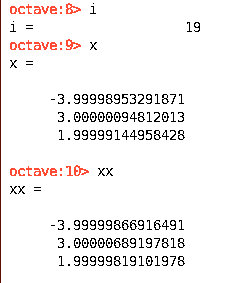
即精确解为 x = ( − 4 , 3 , 2 ) T x = (-4,3,2)^T x=(−4,3,2)T 。
Gauss-Seidel迭代
其矩阵迭代形式为:
x ( k + 1 ) = B G ⋅ x ( k ) + f G B G = ( D − L ) − 1 ⋅ U , f G = ( D − L ) − 1 ⋅ b x^{(k+1)} = B_G \cdot x^{(k)} + f_G\\ B_G = (D - L) ^{-1} \cdot U, \quad f_G = (D - L) ^{-1} \cdot b x(k+1)=BG⋅x(k)+fGBG=(D−L)−1⋅U,fG=(D−L)−1⋅b
使用Matlab编程求解:
d = [5,0,0;0,4,0;0,0,10];
l = [0,0,0;1,0,0;-2,3,0];
u = [0,-2,-1;0,0,-2;0,0,0];
b = [-12;20;3];
t = inv(d - l);
bg = t * u;
fg = t * b;
x = [0;0;0];
xx = [-2.4;4.4;2.1];
i = 0;
while norm(x - xx, inf) >= 1e-5
x = xx;
xx = bg * x + fg;
i = i +1;
end
运行结果为:
同样求得精确解为 x = ( − 4 , 3 , 2 ) T x = (-4,3,2)^T x=(−4,3,2)T 。
边栏推荐
猜你喜欢

搭建frp进行内网穿透

如何高效开发一款微信小程序
Only the background of famous universities and factories can programmers have a way out? Netizen: two, big factory background is OK

JSP intelligent community property management system

Oracle EBS数据库监控-Zabbix+zabbix-agent2+orabbix
Pratique et réflexion sur l'entrepôt de données hors ligne et le développement Bi

Explain in detail the process of realizing Chinese text classification by CNN

Yaml file of ingress controller 0.47.0
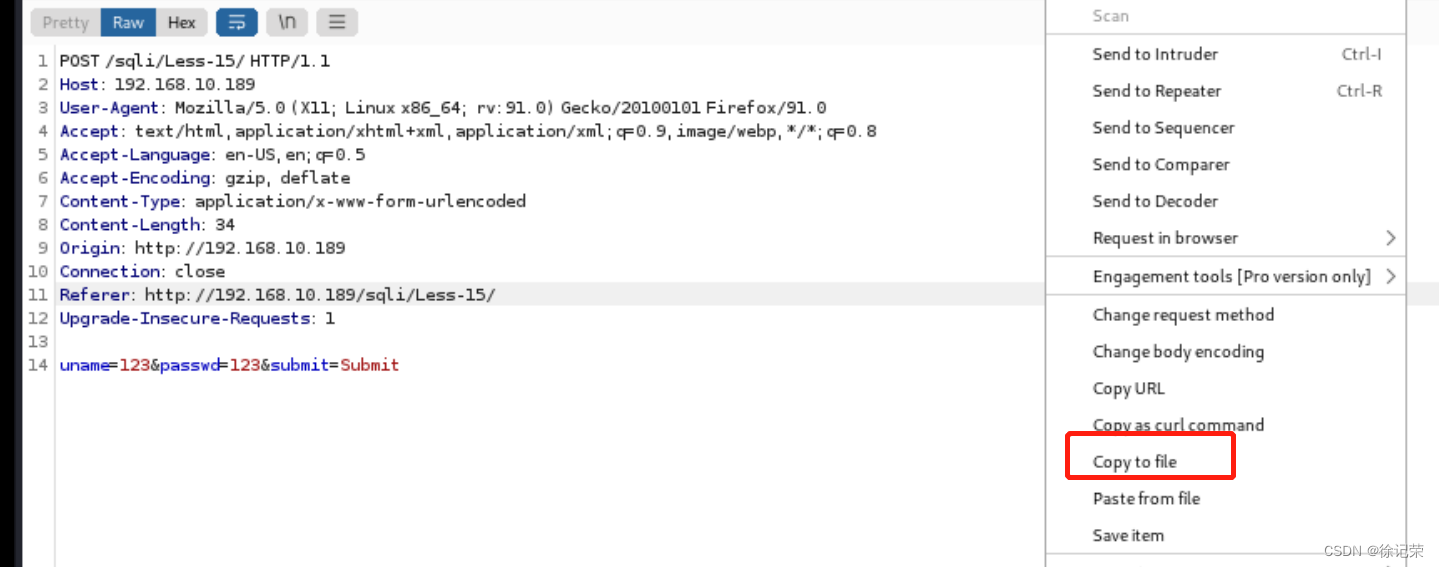
SQLI-LABS通关(less15-less17)
Illustration of etcd access in kubernetes
随机推荐
php中生成随机的6位邀请码
php中时间戳转换为毫秒以及格式化时间
SSM学生成绩信息管理系统
Proteus -- RS-232 dual computer communication
UEditor . Net version arbitrary file upload vulnerability recurrence
Oracle 11.2.0.3 handles the problem of continuous growth of sysaux table space without downtime
Oracle EBS interface development - quick generation of JSON format data
Error in running test pyspark in idea2020
The boss said: whoever wants to use double to define the amount of goods, just pack up and go
pm2简单使用和守护进程
php中在二维数组中根据值返回对应的键值
Oracle RMAN automatic recovery script (migration of production data to test)
ssm超市订单管理系统
MySQL中的正则表达式
Oracle段顾问、怎么处理行链接行迁移、降低高水位
数仓模型事实表模型设计
如何高效开发一款微信小程序
ssm人事管理系统
ORACLE EBS接口开发-json格式数据快捷生成
Network security -- intrusion detection of emergency response