当前位置:网站首页>The boss said: whoever wants to use double to define the amount of goods, just pack up and go
The boss said: whoever wants to use double to define the amount of goods, just pack up and go
2022-07-02 07:03:00 【Javaesandyou】
Let's look at the phenomenon first
Involving such as float perhaps double The processing of these two floating-point data , There will always be some Strange phenomenon , I wonder if you have noticed , Give me a few common chestnuts :
Typical phenomena ( One ): Conditional judgment exceeds expectations
System.out.println( 1f == 0.9999999f ); // Print :false
System.out.println( 1f == 0.99999999f ); // Print :true what ?Typical phenomena ( Two ): Data conversion exceeded expectations
float f = 1.1f;
double d = (double) f;
System.out.println(f); // Print :1.1
System.out.println(d); // Print :1.100000023841858 what ?Typical phenomena ( 3、 ... and ): The basic operation is better than expected
System.out.println( 0.2 + 0.7 );
// Print :0.8999999999999999 what ?Typical phenomena ( Four ): The data increased more than expected
float f1 = 8455263f;
for (int i = 0; i < 10; i++) {
System.out.println(f1);
f1++;
}
// Print :8455263.0
// Print :8455264.0
// Print :8455265.0
// Print :8455266.0
// Print :8455267.0
// Print :8455268.0
// Print :8455269.0
// Print :8455270.0
// Print :8455271.0
// Print :8455272.0
float f2 = 84552631f;
for (int i = 0; i < 10; i++) {
System.out.println(f2);
f2++;
}
// Print :8.4552632E7 what ? No +1 Did you? ?
// Print :8.4552632E7 what ? No +1 Did you? ?
// Print :8.4552632E7 what ? No +1 Did you? ?
// Print :8.4552632E7 what ? No +1 Did you? ?
// Print :8.4552632E7 what ? No +1 Did you? ?
// Print :8.4552632E7 what ? No +1 Did you? ?
// Print :8.4552632E7 what ? No +1 Did you? ?
// Print :8.4552632E7 what ? No +1 Did you? ?
// Print :8.4552632E7 what ? No +1 Did you? ?
// Print :8.4552632E7 what ? No +1 Did you? ?You see , These simple scenarios are difficult to meet our needs , So use floating point numbers ( Include double and float) There are many problems to deal with Obscure pit Waiting for us !
No wonder the technical director made harsh remarks : Who dares to deal with things like The amount of goods 、 Order transaction 、 as well as Monetary calculation Time use floating point data (double/float), Just let us go !

What's the reason ?
Let's take the first typical phenomenon as an example to analyze :
System.out.println( 1f == 0.99999999f );Compare directly with code 1 and 0.99999999, Actually print out true!

What does that mean ? This shows that computers are not at all I can't tell These two numbers . Why is that ?
We might as well think briefly :
We know that these two floating-point numbers are only the specific values seen by human eyes , Is what we usually understand as a decimal number , But the bottom of the computer does not calculate according to the decimal system , Anyone who has learned the basic group counting principle knows , The bottom of the computer is ultimately based on things like 010100100100110011011 such 0、1 Binary to complete .
So in order to understand the actual situation , We should put these two decimal floating-point numbers Convert to binary space Take a look at .
Decimal floating point number to binary How to turn 、 How to calculate , I think this should belong to basic computer base conversion common sense , stay 《 The principle of computer organization 》 I must have learned in similar classes , I won't repeat it here , Give the result directly ( Convert it to IEEE 754 Single precision 32-bit, It's just float The precision corresponding to the type )
1.0( Decimal system )
↓
00111111 10000000 00000000 00000000( Binary system )
↓
0x3F800000( Hexadecimal )0.99999999( Decimal system )
↓
00111111 10000000 00000000 00000000( Binary system )
↓
0x3F800000( Hexadecimal )Sure enough , The underlying binary representation of these two decimal floating-point numbers is the same , It's no wonder that == The judgment result of returns true!
however 1f == 0.9999999f The result returned is expected , Print false, We also convert them to binary mode to see what happens :
1.0( Decimal system )
↓
00111111 10000000 00000000 00000000( Binary system )
↓
0x3F800000( Hexadecimal )0.9999999( Decimal system )
↓
00111111 01111111 11111111 11111110( Binary system )
↓
0x3F7FFFFE( Hexadecimal )Oh , Obviously , The binary representation of the two is really different , This is a logical result .
So why 0.99999999 The underlying binary representation of is :00111111 10000000 00000000 00000000 Well ?
This is not a floating point number 1.0 Binary representation of ?
This is about the precision of floating point numbers .
The precision of floating point numbers !
Did you learn 《 The principle of computer organization 》 Everyone in this class should know , The storage of floating-point numbers in the computer follows IEEE 754 Floating point count standard , It can be expressed by scientific counting as :

Just give : Symbol (S)、 Step code part (E)、 Mantissa part (M) The information of these three dimensions , The representation of a floating point number is completely determined , therefore float and double Floating point numbers are stored in the following two memory structures :


、 The symbolic part (S)
0- just 1- negative
2、 Step code part (E)( Index part ):
- about float Type floating point number , Index part 8 position , Consider positive and negative , Therefore, the index range that can be expressed is -127 ~ 128
- about double Type floating point number , Index part 11 position , Consider positive and negative , Therefore, the index range that can be expressed is -1023 ~ 1024
3、 Mantissa part (M):
The precision of a floating-point number is determined by the number of bits of the mantissa :
- about float Type floating point number , Mantissa part 23 position , Conversion to decimal is 2^23=8388608, So the decimal precision is only 6 ~ 7 position ;
- about double Type floating point number , Mantissa part 52 position , Conversion to decimal is 2^52 = 4503599627370496, So the decimal precision is only 15 ~ 16 position
So for the above values 0.99999999f, It's obviously more than float Precision range of type floating-point data , Problems are inevitable .
How to solve the problem of accuracy
So if it involves The amount of goods 、 Transaction value 、 Monetary calculation What should we do in such a scene that requires high accuracy ?
Method 1 : Use string or array to solve multi bit number problem
All the partners who have brushed the algorithm problems should know , Using strings or arrays to represent large numbers is a typical problem-solving idea .
For example, classic interview questions : Write the addition of two arbitrary large numbers 、 Subtraction 、 Multiplication and so on .
At this time, we can use strings or arrays to represent such large numbers , Then the specific calculation process is simulated manually according to the rules of four operations , We also need to consider various factors such as : carry 、 Borrow position 、 Symbol And so on , It's really complicated , This article does not elaborate .
Method 2 :Java The large number of categories is a good thing
JDK We have already considered the calculation accuracy of floating-point numbers , Therefore, it provides a special for high-precision numerical calculation Class of large numbers To facilitate our use .
In the foreword 《 To be honest with you , I recently talked to Java The source code is on the bar 》 Said in ,Java A large number of classes are located in java.math It's a bag :

You can see , frequently-used BigInteger and BigDecimal It is a sharp tool for dealing with high-precision numerical calculation .
BigDecimal num3 = new BigDecimal( Double.toString( 1.0f ) );
BigDecimal num4 = new BigDecimal( Double.toString( 0.99999999f ) );
System.out.println( num3 == num4 ); // Print false
BigDecimal num1 = new BigDecimal( Double.toString( 0.2 ) );
BigDecimal num2 = new BigDecimal( Double.toString( 0.7 ) );
// Add
System.out.println( num1.add( num2 ) ); // Print :0.9
// reduce
System.out.println( num2.subtract( num1 ) ); // Print :0.5
// ride
System.out.println( num1.multiply( num2 ) ); // Print :0.14
// except
System.out.println( num2.divide( num1 ) ); // Print :3.5Yes, of course , image BigInteger and BigDecimal The operation efficiency of this large number class is certainly not as efficient as that of the native type , The price is still relatively expensive , The selection needs to be evaluated according to the actual scene .
by the way , Let's talk about it here , I'm currently on the job Java Development , If you are learning now Java, understand Java, Eager to be a qualified Java Development Engineer , At the beginning of learning Java The process of the lack of basic introductory video tutorial , You can follow me and write to me personally :01. obtain . I have the latest Java Basic complete video tutorial .
边栏推荐
- Code execution sequence with and without resolve in promise
- JS divides an array into groups of three
- Latex warning: citation "*****" on page y undefined on input line*
- 2021-07-17C#/CAD二次开发创建圆(5)
- Build FRP for intranet penetration
- ts和js区别
- php中获取汉字拼音大写首字母
- SQLI-LABS通关(less6-less14)
- pySpark构建临时表报错
- Go common compilation fails
猜你喜欢

Latex在VSCODE中编译中文,使用中文路径问题解决

Solve the problem of bindchange event jitter of swiper component of wechat applet
How to call WebService in PHP development environment?

Build FRP for intranet penetration

Write a thread pool by hand, and take you to learn the implementation principle of ThreadPoolExecutor thread pool

Utilisation de la carte et de foreach dans JS

The table component specifies the concatenation parallel method

Wechat applet Foundation
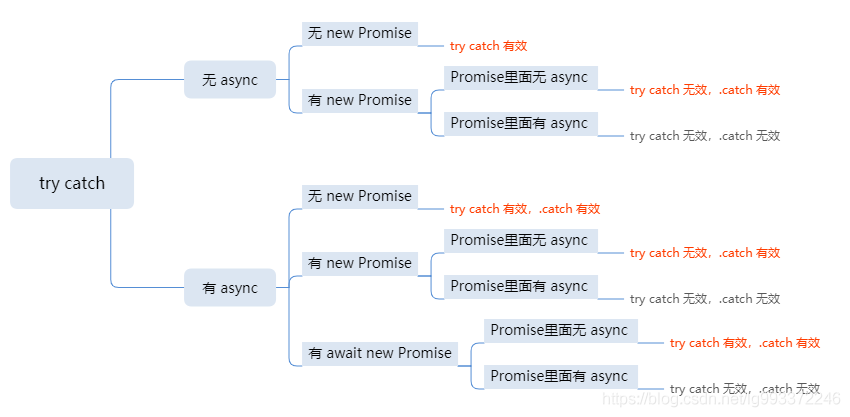
js中对于返回Promise对象的语句如何try catch

uniapp引入本地字体
随机推荐
Record RDS troubleshooting once -- RDS capacity increases dramatically
Ingress Controller 0.47.0的Yaml文件
PIP install
Recursion (maze problem, Queen 8 problem)
JS countdown case
Eggjs -typeorm treeenity practice
蚂蚁集团g6初探
Oracle rman自动恢复脚本(生产数据向测试迁移)
PM2 simple use and daemon
Laravel8中的find_in_set、upsert的使用方法
Fe - eggjs combined with typeorm cannot connect to the database
2021-07-19c CAD secondary development creates multiple line segments
php中在二维数组中根据值返回对应的键值
table 组件指定列合并行方法
CAD二次开发 对象
Sentry搭建和使用
数仓模型事实表模型设计
Write a thread pool by hand, and take you to learn the implementation principle of ThreadPoolExecutor thread pool
Latex在VSCODE中编译中文,使用中文路径问题解决
UEditor .Net版本任意文件上传漏洞复现