当前位置:网站首页>余弦距离介绍
余弦距离介绍
2022-08-03 19:08:00 【xiaozheng123121】
目录
作者:CSDN博主「深度学习视觉」
原文链接:https://blog.csdn.net/lucky_kai/article/details/89514868
————————————————
概述: 在机器学习领域中,通常将特征表示为向量的形式,所以在分析两个特征向量之间的相似性时,常用余弦相似度表示。
例如将两篇文章向量化,余弦距离可以避免因为文章的长度不同而导致距离偏大,余弦距离只考虑两篇文章生成的向量的夹角。
余弦相似度的取值范围是[-1,1],相同两个向量的之间的相似度为1。
余弦距离的取值范围是[0,2]。
余弦相似度的定义公式为 c o s ( A , B ) = A ⋅ B ∥ A ∥ 2 ∥ B ∥ 2 cos(A,B)=\frac{A\cdot B}{\left\|A \right\|_2\left\|B \right\|_2} cos(A,B)=∥A∥2∥B∥2A⋅B
归一化后: ∥ A ∥ 2 = 1 , ∥ B ∥ 2 = 1 , ∥ A ∥ 2 ∥ B ∥ 2 = 1 \left\|A\right\|_2=1, \left\|B\right\|_2=1, \left\|A\right\|_2\left\|B\right\|_2=1 ∥A∥2=1,∥B∥2=1,∥A∥2∥B∥2=1
余弦距离: d i s t ( A , B ) = 1 − c o s ( A , B ) = ∥ A ∥ 2 ∥ B ∥ 2 − A ⋅ B ∥ A ∥ 2 ∥ B ∥ 2 dist(A,B)=1-cos(A,B)=\frac{\left\|A \right\|_2\left\|B \right\|_2-A\cdot B}{\left\|A \right\|_2\left\|B \right\|_2} dist(A,B)=1−cos(A,B)=∥A∥2∥B∥2∥A∥2∥B∥2−A⋅B,距离恒大于0
欧式距离: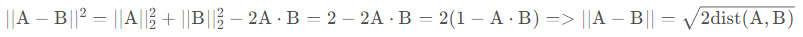
由公式可以看出归一化后,欧式距离与余弦距离存在单调性关系。此时两种距离的值域都为[0,2]。
欧式距离与余弦距离的对比:
1.欧式距离的数值受到维度的影响,余弦相似度在高维的情况下也依然保持低维完全相同时相似度为1等性质。
2.欧式距离体现的是距离上的绝对差异,余弦距离体现的是方向上的相对差异。
边栏推荐
- Postgresql source code (65) analysis of the working principle of the new snapshot system Globalvis
- MySQL【变量、流程控制与游标】
- G6尝试 学习
- 阿里巴巴政委体系-第八章、阿里政委工作方法论
- 懵逼!阿里一面被虐了,幸获内推华为技术四面,成功拿到offer,年薪40w
- 深度学习常用公式与命令总结(更新中)
- unity3d-游戏物体控制方法
- Word另存为PDF后无导航栏解决办法
- The ecological environmental protection management system based on mobile GIS
- 力扣刷题之合并两个有序数组
猜你喜欢
When does MySQL use table locks and when to use row locks?You should know this

Mkke:为什么无法从Oracle 11g或12c升级到Oracle 23c?
【夜莺监控方案】08-监控msyql集群(prometheuse+n9e+mysqld_exporter)
字节跳动三面拿offer:网络+IO+redis+JVM+GC+红黑树+数据结构,助你快速进大厂!!
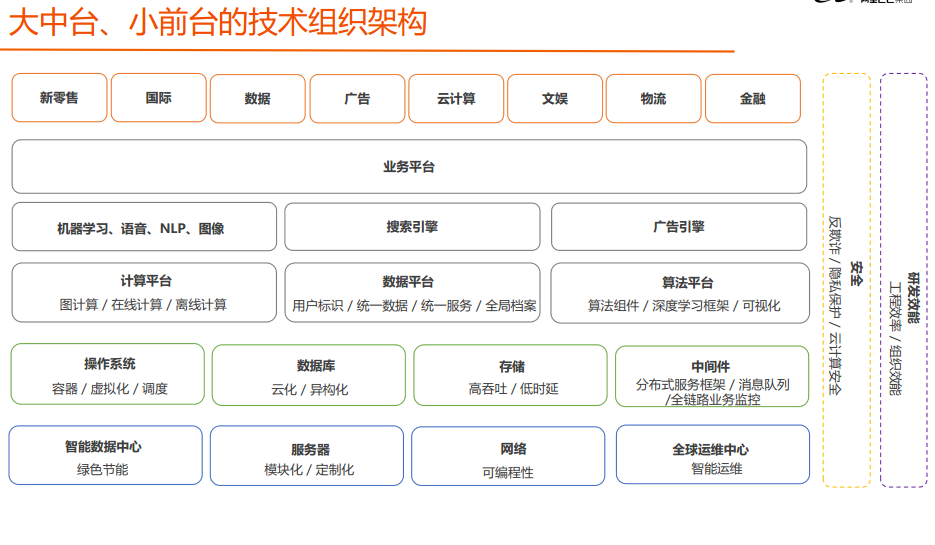
Zhong Hua, senior architect of Ali: China-Taiwan strategic thinking and architecture practice; including internal implementation manual
MD5是对称加密还是非对称加密,有什么优缺点
开发即时通讯到底需要什么样的技术,需要多久的时间
![[Azure Event Hub] Create Event Hub Consume Client + Custom Event Position with Azure AD Authentication](/img/fe/db506853be08398f815f4e36beee76.png)
[Azure Event Hub] Create Event Hub Consume Client + Custom Event Position with Azure AD Authentication
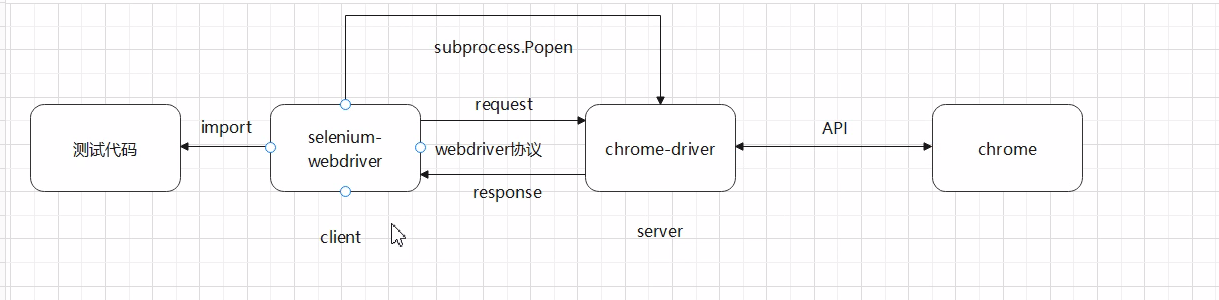
C#爬虫之通过Selenium获取浏览器请求响应结果
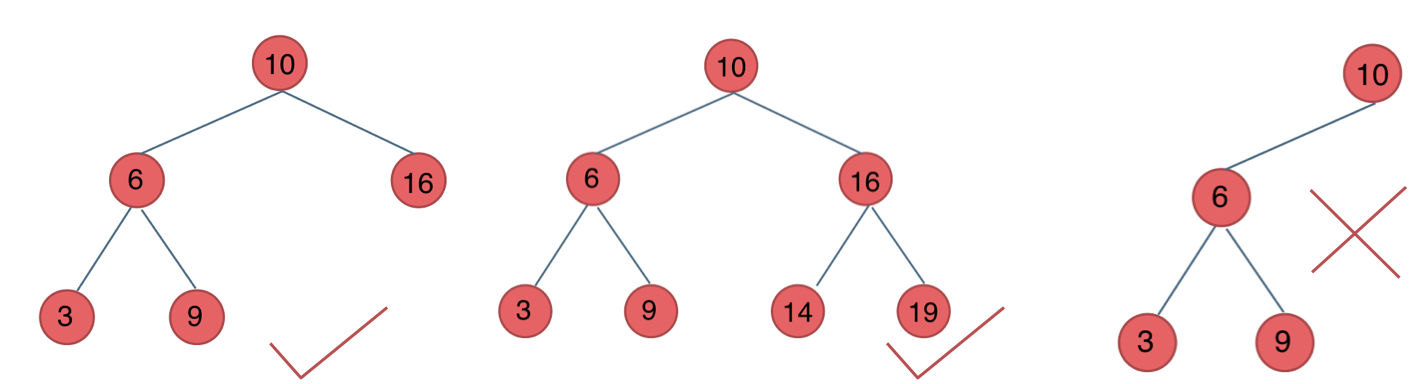
BinomialTree 二叉树
随机推荐
ADS 2023 下载链接
Power button brush the topic of merging two orderly array
ctfshow php特性
SQL server 实现触发器备份表数据
CC2530_ZigBee+华为云IOT:设计一套属于自己的冷链采集系统
梅科尔工作室-14天华为培训七
阿里巴巴政委体系-第八章、阿里政委工作方法论
面试突击:什么是粘包和半包?怎么解决?
Protobuf Grpc使用异常 类型有未导出的方法,并且是在不同的软件包中定义
pytest接口自动化测试框架 | Jenkins集成初探
MySQL超详细安装教程 手把手教你安装MySQL到使用MySQL 最简单的MySQL安装方式,这种方式装,卸载也简单
Difference差分数组
Postgresql-xl全局快照与GTM代码走读(支线)
InnoDB 中不同SQL语句设置的锁
Shell编程案例
Postgresql中的pg_memory_barrier_impl和C的volatile
MySQL 啥时候用表锁,啥时候用行锁?这些你都应该知道吧
要想成为黑客,离不开这十大基础知识
Postgresql源码(65)新快照体系Globalvis工作原理分析
力扣刷题之数组序号计算(每日一题7/28)