选出表中的中位数记录[构造左右边界 || 问题转换]

前言

对于选表中的中位数记录，或者说中位数落在了那一块记录，该如何解？可构造左右边界 || 问题转换（正序累计&反序累计都大于中值时该记录为中位数记录）。

一、中位数问题

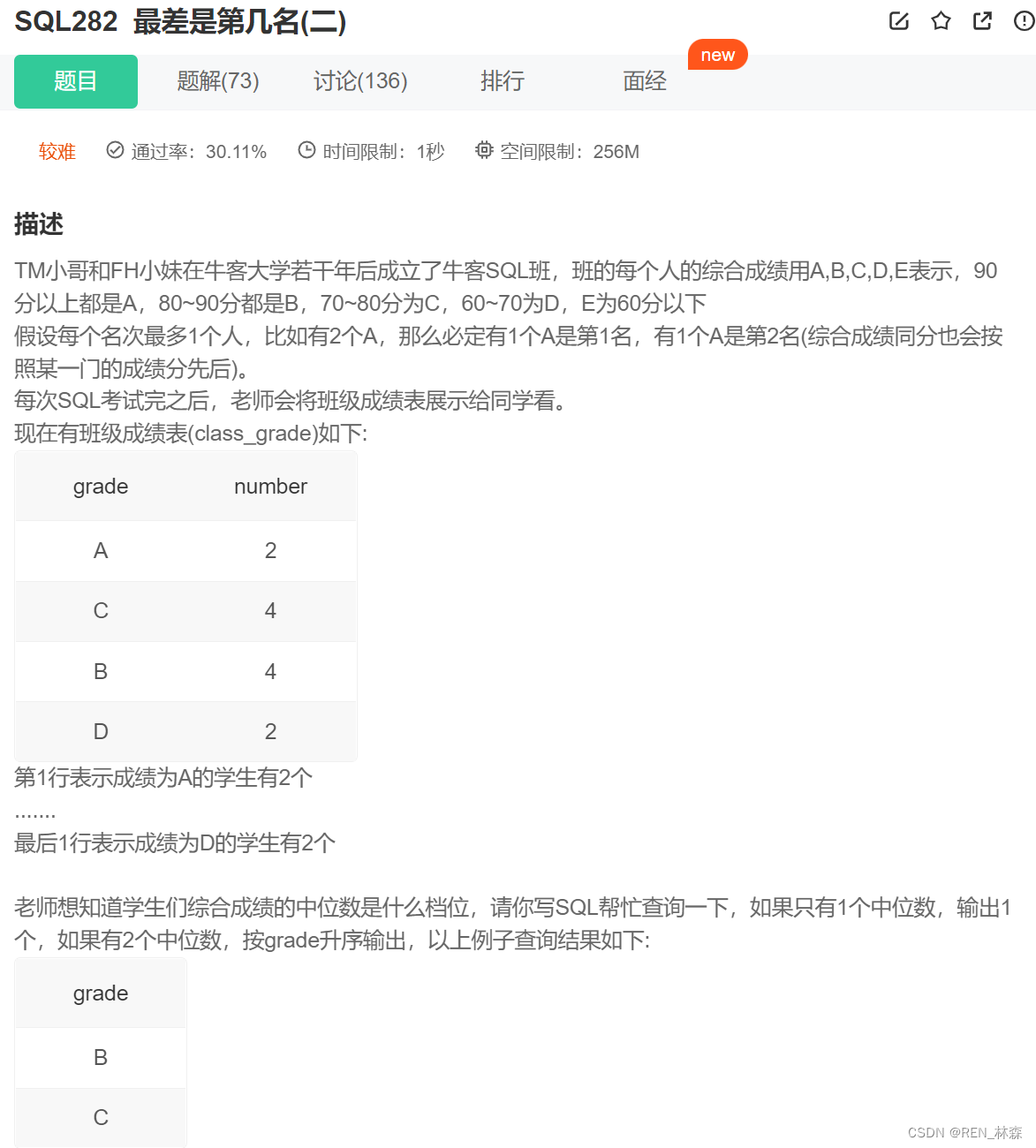
二、构造边界 & 问题转换

分两类思想，一类构造左右边界 & 中值；一类问题转化，反向思考，当正序累计 & 逆序累计都大于中值时，则为中位数。

解1：两层view + lead()构造左右边界

with view4base as(
    select
        grade,
        sum(number) over(order by grade) `right`,
        sum(number) over() total
    from class_grade
),view4lead as(
    select
        grade,total,
        lead(`right` + 1,1)  over(order by `right` desc) `left`,`right`
    from view4base 
)
select grade
from view4lead
where (total >> 1) + 1 >= `left` and (total >> 1) + 1 <= `right`
    or total & 1 = 0 and (total >> 1) >= `left` and (total>>1) <= `right`
order by grade

解2：直接做运算得到想要的值–左边界。

with view4base as(
    select
        grade,
        sum(number) over(order by grade) - number `left`,
        sum(number) over(order by grade) + 1 `right`,
        sum(number) over() total
    from class_grade
)
select grade
from view4base
where (total >> 1) + 1 > `left` and (total >> 1) + 1 < `right`
    or total & 1 = 0 and (total >> 1) > `left` and (total >> 1) < `right`
order by grade

解3：中位数：n + 1 / 2 和 n / 2 + 1

with view4base as(
    select
        grade,
        sum(number) over(order by grade) - number `left`,
        sum(number) over(order by grade) + 1 `right`,
        # 中位数：n + 1 / 2 和 n / 2 + 1
         sum(number) over() +  1 >> 1 mid1,
        (sum(number) over() >> 1) + 1 mid2
    from class_grade
)
select grade
from view4base
where mid1 > `left` and mid1 < `right` or mid2 > `left` and mid2 < `right`
order by grade

解4：当一个数正序 & 逆序累计都大于等于中值时(非取整，保留0.5)，这个数为中位数。

with view4base as(
    select
        grade,
        sum(number) over(order by grade) m,
        sum(number) over(order by grade desc) n,
        sum(number) over() / 2  mid
    from class_grade
)
select grade
from view4base
where m >= mid and n >= mid
order by grade

总结

1）中位数问题思路，构造左右边界 & 问题转换。
2）抽象能力很重要，不管是聚集函数/窗口函数/内置函数，入参&结果不过可看成一个值，再上面做四则运算/函数等都是OK的，抽象的看待问题。

参考文献

[1] LeetCode 最差是第几名(二)