[Paper Notes KDD2021] MixGCF: An Improved Training Method for Graph Neural Network-based Recommender Systems

学习总结

零、论文简介

论文题目：MixGCF: An Improved Training Method for Graph Neural Network-based Recommender Systems
论文链接：http://keg.cs.tsinghua.edu.cn/jietang/publications/KDD21-Huang-et-al-MixGCF.pdf
论文代码：https://github.com/huangtinglin/MixGCF
论文作者：Tinglin Huang,Teacher Tang Jie and others

一、Introduction

导言：GNN被广泛应用于embeddinggenerated scene,对user和item分别进行embedding化,使用双塔模型;类似像Graphsage、PinSage、LightGCNAlgorithms such as these have also been used in recommender systems in the industry,但是GNNThe negative sampling technique is still to be studied,Most algorithms in the past select negative samples from real data,而忽略了embedding的信息,而MixGCFis data augmented、Aggregate methods obtain negative samples and their representations.NGCF和LightGCN在使用MixGCF后,在NDCG指标上分别提高了26%和22%.

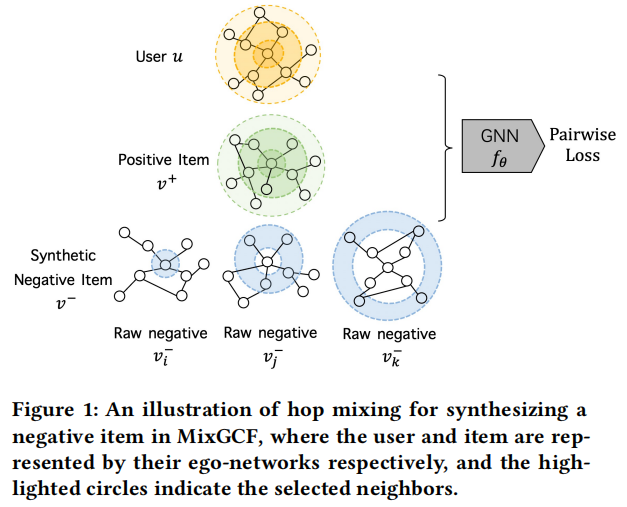
1.1 聚合 Aggregation

聚合过程：$${\mathbf{e}}_u^{(l+1)}=\sum _{i\in N_u}\frac{1}{\sqrt{\left|N_u\right|\left|N_i\right|}}{\mathbf{e}}_i^{(l)},{\mathbf{e}}_v^{(l+1)}=\sum _{j\in N_v}\frac{1}{\sqrt{\left|N_v\Vert N_j\right|}}{\mathbf{e}}_j^{(l)}$$

1.2 池化过程

池化过程：$${\mathbf{e}}_u^{\ast }=\sum _{l=0}^L{\lambda }_l{\mathbf{e}}_u^{(l)},{\mathbf{e}}_v^{\ast }=\sum _{l=0}^L{\lambda }_l{\mathbf{e}}_v^{(l)}$$

1.3 Negative sampling optimization

一般LTRThe loss function for the task is BPR loss：$$\max \prod _{v^{+},v^{-}\sim f_S(u)}{P}_u\left(v^{+}>v^{-}\mid \Theta \right)$$
其中参数：

• $v^{+}$和$v^{}-$分别表示positive items和negative items
• $P_u(a>b)$表示用户u,相比于item b来说,more preferreditem a
• $f_S(u)$是negative sampling的分布,Many recommendation algorithms（如LightGCN、NCF、BPR、NGCF等算法）都是将negative sample服从于uniform均匀分布（$f_S(u)=f_{\text{uniform }}(u)$）

1.4 Negative sampling problem

• 经典的BPR loss栗子.
• Negative sampling is generally useduniform distribution,为了改进GNN的负采样：
  • PinSage根据PageRankThe score is negatively sampled;
  • MCNConsider the structural correlation between positive and negative samples,Re-involved the distribution of positive and negative samples;
  • But these algorithms are only mainly indiscrete graph space中负采样,而忽略了GNN在embeddingA unique neighbor aggregation process in space.
• MixGCFSubject to data augmentation and metric learningthought proposed,进行hard负样本的生成.

二、MixGCF算法

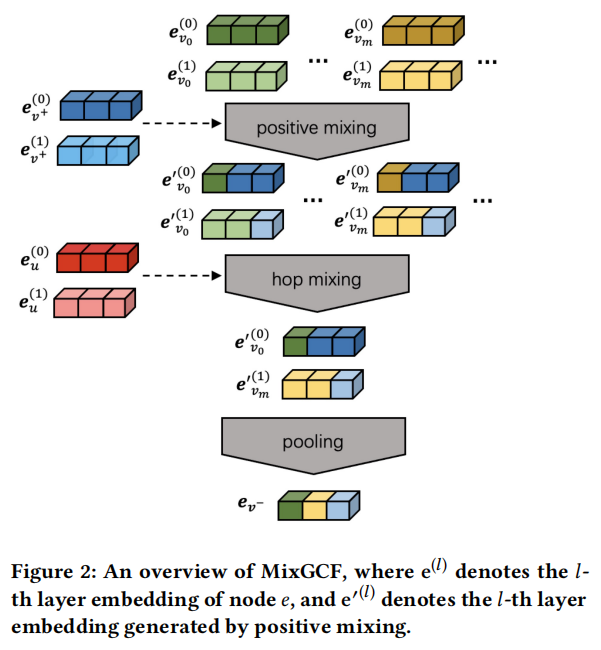
2.1 positive mixing

positive mixing的操作：$${\mathbf{e}}_{v_m}^{\prime (l)}={\alpha }^{(l)}{\mathbf{e}}_{v^{+}}^{(l)}+\left(1-{\alpha }^{(l)}\right){\mathbf{e}}_{v_m}^{(l)},{\alpha }^{(l)}\in (0,1)$$
其中参数：

• ${\alpha }^{(l)}$是每一个hopuniformly sampledmixing因子;
• mixup的mixingfactor is frombeta分布$\mathrm{Beta}(\beta ,\beta )$sampled from,It has a great impact on the generalization ability of the model;
• In order to alleviate this effect mentioned above,positive mixing中的mixing因子${\alpha }^{(l)}$统一从(0, 1)sampling from the distribution;
• ${\mathcal{E}}^{\prime }$是候选negatives M增强后的embedding集合.

positive mixing增强negatives通过以下两种方式：
1）把positive information注射到negative samples,This helps to force the optimization algorithm to work harder、More aggressive use of decision boundaries.
2）用mixingFactors introduce random uncertainty into them.

2.2 Hop Mixing

2.3 optimization with MixGCF

$${\mathcal{L}}_{\mathrm{BPR}}=\sum _{\begin{array}{c}\left(u,v^{+}\right)\in O^{+}\\ {\mathbf{e}}_{v^{-}}\sim f_{\mathrm{MixGCF}}\left(u,v^{+}\right)\end{array}}\ln \sigma \left({\mathbf{e}}_u\cdot {\mathbf{e}}_{v^{-}}-{\mathbf{e}}_u\cdot {\mathbf{e}}_{v^{+}}\right)$$

2.4 关于MixGCF的相关讨论

2.5 时间复杂度

三、实验环节

3.1 experimental settings

（1）评估指标

（2）推荐算法模型

（3）Baselines

（4）超参数设置

3.2 Performance comparison

实验结果对比：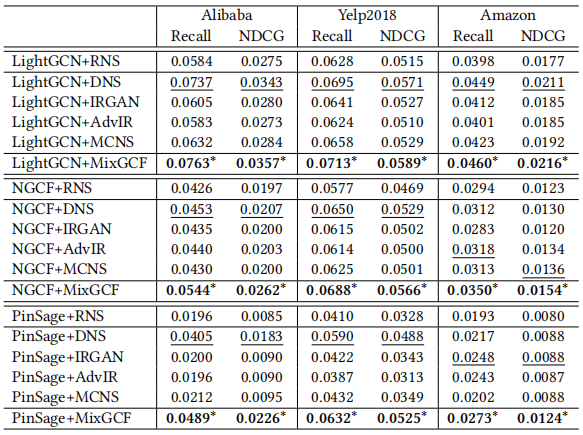

（1）running time

（2）running time

四、相关工作

4.1 基于GNN的推荐算法

• PinSage、GC-MC、NGCF、LightGCN
• 利用side info：社交网络、知识图谱 …

4.2 推荐系统中的负采样

• Static Sampler Negative sampling from a fixed distribution
  • 均匀分布、流行度 指数 3/4
• GAN-based Sampler Negative sampling based on generative adversarial networks
  • IRGAN、KBGAN、AdvIR
• Hard Negative Sampler Adaptively selected for the current user hardest 负样本
  • DNS
• Graph-based Sampler Negative sampling based on graph information
  • MCNS、KGPolicy、PinSage（基于Personalized PageRank）

Reference

[1] http://keg.cs.tsinghua.edu.cn/jietang/publications/KDD21-Huang-et-al-MixGCF.pdf
[2] https://huangtinglin.github.io/experience/
[3] Bayesian Personalized Sorting AlgorithmBPR