当前位置:网站首页>Link with Game Glitch
Link with Game Glitch
2022-08-02 07:49:00 【to cling】
Problem
给出n种物品,These items can be converted.给出m条转换规则,形如: a a a 个 b b b 物品 可以转换为 c × w c \times w c×w 个 d d d 物品.问: w w w How much to take,In order to prevent these items from being converted into an infinite number of items.
Solution
It's obviously a graph theory question.边: c → d c \to d c→d, 边权: c w a \frac{cw}{a} acw
- To make it impossible to convert into an infinite number of items,Then it is necessary to determine whether such one exists“环”.
假设:The edge weights on this ring are e i e_i ei, 环上有 k k k 个节点
那么,当满足 e 1 × e 2 × . . . × e k > 1 e_1 \times e_2 \times ... \times e_k > 1 e1×e2×...×ek>1 时, can be converted into an infinite number of items - 考虑到精度问题,Logarithms can be taken left and right
l o g ( e 1 × e 2 × . . . × e k ) > l o g ( 1 ) = 0 log(e_1 \times e_2 \times ... \times e_k) > log(1) = 0 log(e1×e2×...×ek)>log(1)=0
即: l o g ( e 1 ) + l o g ( e 2 ) + . . . + l o g ( e k ) > 0 − l o g ( e 1 ) − l o g ( e 2 ) − . . . − l o g ( e k ) < 0 log(e_1) + log(e_2) + ... + log(e_k) > 0 \\ -log(e_1) - log(e_2) - ... - log(e_k) < 0 log(e1)+log(e2)+...+log(ek)>0−log(e1)−log(e2)−...−log(ek)<0
到此为止,The title has been converted to side weights − l o g ( w c a ) -log(\frac {wc}{a}) −log(awc) the negative loop problem - 最后注意:The figure may be “森林“结构.
Code
const int N = 4e3 + 3;
int n, m;
int h[N], net[N], e[N], a[N], c[N], tot;
void add(int x, int y, int z, int zz)
{
e[++tot] = y;
a[tot] = z; c[tot] = zz;
net[tot] = h[x];
h[x] = tot;
}
double d[N];
int v[N], vis[N], cnt[N];
//vMarks whether the point is in the queue
//visMarks whether the point has been traveled,Used to traverse the forest structure
//cntThe number of updates to mark the point,更新次数 >= n 则存在负环
bool spfa(double w)
{
for (int i = 1; i <= n; i++)
d[i] = 1e18, v[i] = 0, vis[i] = 0;
for (int i = 1; i <= n; i++)
{
if (vis[i]) continue;
vis[i] = 1;
queue<int> q;
q.push(i);
d[i] = 0; v[i] = 1;
cnt[i] = 0;
while (sz(q))
{
int x = q.front(); q.pop();
v[x] = 0;
for (int i = h[x]; i; i = net[i])
{
int y = e[i]; double z = -log(w * c[i] / a[i]);
if (d[y] > d[x] + z)
{
vis[x] = 1;//标记走过的点
cnt[y] = cnt[x] + 1;
if (cnt[y] >= n) return 0;//find the negative ring
d[y] = d[x] + z;
if (v[y] == 0) q.push(y), v[y] = 1;
}
}
}
}
return 1;
}
int main()
{
IOS;
cin >> n >> m;
for (int i = 1, a, b, c, d; i <= m; i++)
{
cin >> a >> b >> c >> d;
add(b, d, a, c);
}
double l = 0, r = 1;
while (r - l > esp)
{
double mid = (l + r) / 2;
if (spfa(mid)) l = mid;
else r = mid;
}
cout << fixed << setprecision(10) << r << endl;
return 0;
}
边栏推荐
猜你喜欢
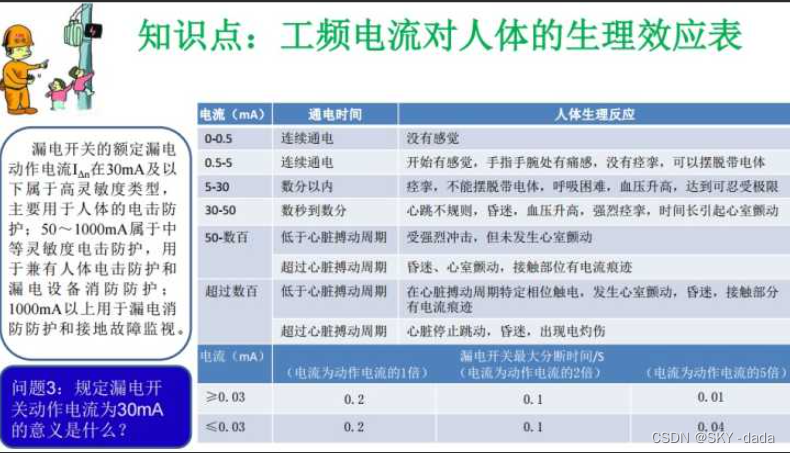
逆变器绝缘检测检测功能及软件实现
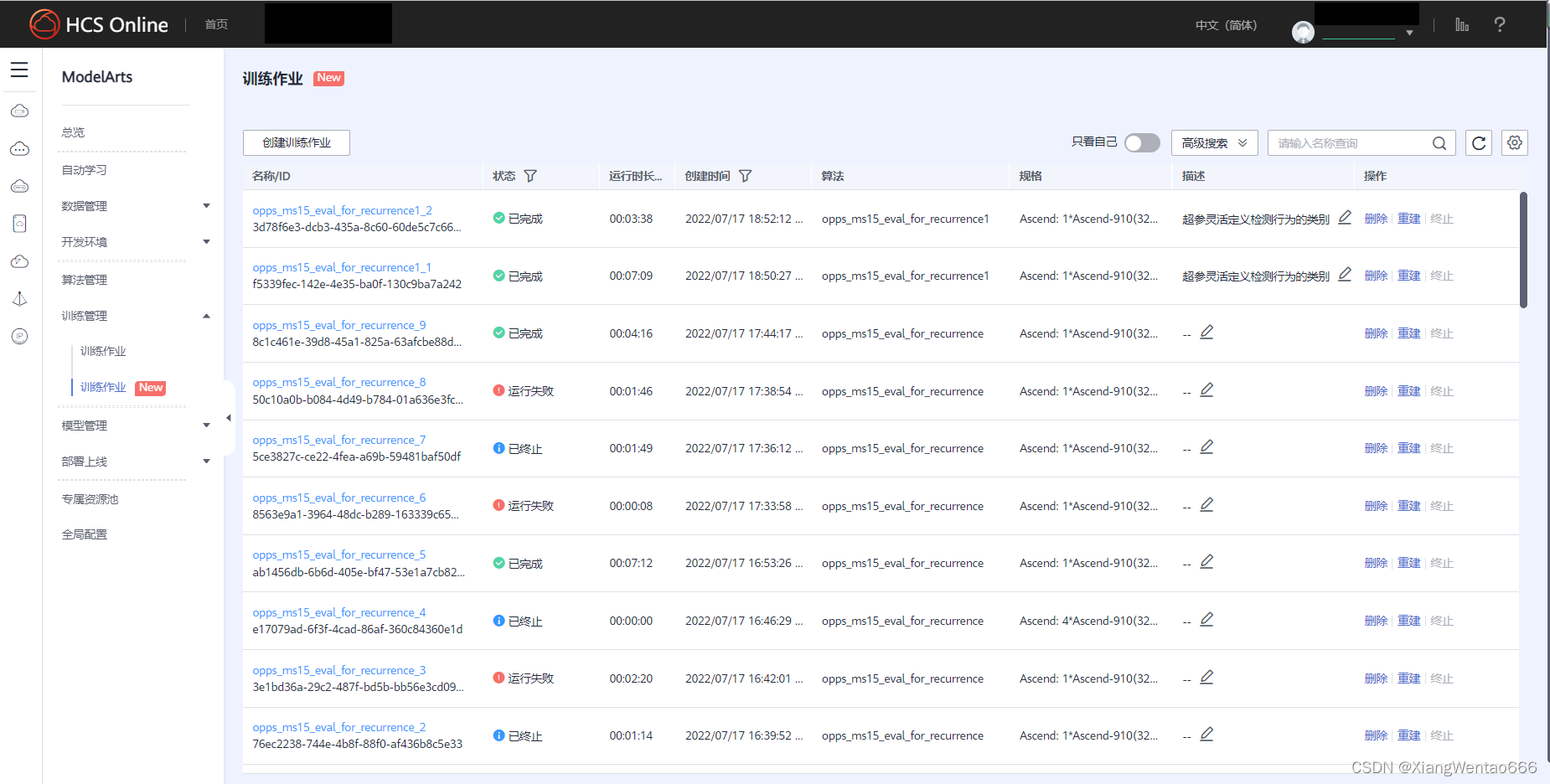
企业实训复现指导手册——基于华为ModelArts平台的OpenPose模型的训练和推理、基于关键点数据实现对攀爬和翻越护栏两种行为的识别、并完成在图片中只标注发生行为的人

实例027:递归输出
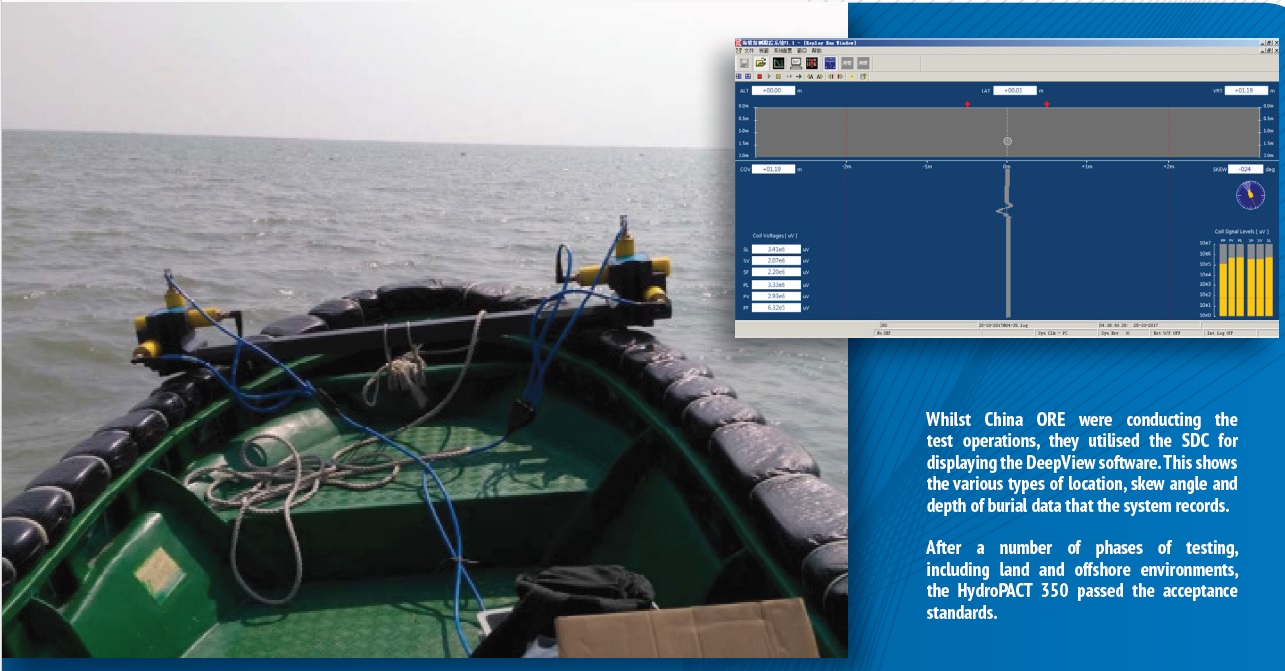
海缆探测仪TSS350(二)

MySQL-索引优化和查询优化

论文阅读 (64):Weakly-supervised Video Anomaly Detection with Robust Temporal Feature Magnitude Learning
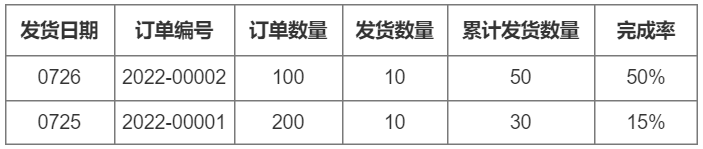
【请教】SQL语句按列1去重来计算列2之和

MySQL-慢查询日志

Gradle系列——Gradle插件(基于Gradle文档7.5)day3-2

2022.07.31(LC_6132_使数组中所有元素都等于零)
随机推荐
2022.07.31(LC_6132_使数组中所有元素都等于零)
跨阻放大器
封装class类一次性解决全屏问题
【CNN回归预测】基于matlab卷积神经网络CNN数据回归预测【含Matlab源码 2003期】
线程的创建方式
入门opencv,欢笑快乐每一天
Go implements distributed locks
LeetCode 283. 移动零(简单、数组)
堡垒机、堡垒机的原理
雷达人体存在感应器方案,智能物联网感知技术,实时感应人体存在
查看僵尸进程
(Part of it is not understood, and the notes are not completed) [Graph Theory] Difference Constraints
飞桨paddle技术点整理
【机器学习】课程设计布置:某闯关类手游用户流失预测
实例027:递归输出
Gradle系列——Gradle插件(基于Gradle文档7.5)day3-2
【云原生】如何快速部署Kubernetes
“蔚来杯“2022牛客暑期多校训练营5,签到题KBGHFCD
LeetCode 2312. 卖木头块
初探形式化方法基本原理