当前位置:网站首页>Do you really think binary search is easy
Do you really think binary search is easy
2022-07-06 07:21:00 【Walnut is surnamed Hu, and butterfly is also surnamed Hu】
Basic binary search template analysis , Refer to the leetcode A great god labuladong The antithesis of
Here we first introduce the concept of search interval
Standard bisection template
int a[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int target = 0;
cin>>target;
int left = 0;
int right = sizeof(a) / sizeof(a[0]) - 1;//
while(left <= right)//??
{
int mid = (left + right) >> 1;
if(a[mid] == target)
{
return mid;
}
else if(a[mid] < target)
{
left = mid + 1;//??
}
else
{
right = mid - 1;//??
}
}
return -1;// Did not find 1.while Conditions in brackets
What we use here is [ ,] An interval closed on both sides . It's just right It points to the subscript of the last common element . If we use [ , ] Words , Then we while The conditions inside must be written left <= right, It can't be <, Because we have a closed interval here, it means that the condition for the end of the cycle is [left + 1, left], This interval does not exist , So no common elements are missing . But if our ending condition is left < right Words , So the end condition is [left, left], We can find that there are also missing common elements , So it's wrong . This is Search range . Another example , Suppose we write right = sizeof(a) / sizeof(a[0]) Words , So it means [ ,), because right Actually, it doesn't exist , Suppose we write left <= right, So the end condition is [left + 1, left), The interval does not exist , But we cycled once more , And this is more than one cycle Probably It will make the loop fall into a wireless loop . If write left < right, So the end condition is [left , left), There is also nothing missing .
2.left = mid + 1?? right = mid - 1??
Why do you write this ? The reason is simple , Or use the search interval ,[ ,] The scope of our search is [left, mid - 1] and [mid+ 1, right], because mid We have already found , There is no need to look for it again , If you want to put mid Taking it into account may lead to a dead cycle , Because the interval has intersection , If the final result happens to be within the intersection range, it will cycle all the time . But if we use [ , ) Words , So the scope is [left, mid) and [mid + 1, right), you 're right , this is it .
The method of searching the interval is introduced , Next, continue to look down .
#include<iostream>
using namespace std;
int main()
{
int a[] = { 1,2,3,4,5,6,7,8,9,10 };
int left = 0;
int right = sizeof(a) / sizeof(a[0]) - 1;
int target = 0;
cin >> target;
while (left <= right)
{
int mid = (left + right) / 2;
if (a[mid] < target)
{
left = mid;
}
else if (a[mid] > target)
{
right = mid;
}
else
{
cout << mid;
break;
}
}
return 0;
}Of course, for this standard template , We don't follow the rules exactly , Write left = mid,right = mid It's fine too , It's just [left, mid] and [mid, right], It's just that the number of cycles may be a little more .
About binary search
Traditional binary search : Orderly , Find the position of a number . But in fact, binary search is not so rigid , Binary search is just a way to find , The time complexity is zero o(logN), Because when the topic requires time complexity, it must be o(logN) We will probably use two-point search . As a way to find , Binary search adopts the strategy of cutting half each time , Each reduction of half allows us to sort half of the data at one time , Instead of a total or several data , So we should pay more attention to the traditional conditions of binary search , But the strategy of cutting half at a time .

First , We want to be efficient , Cut it in half at one time , Then we must get half the chips cut at one time , When we can cut it in half at a time, it shows that the data has some rules , Order is the simplest rule , This is also one of the reasons why we cannot correctly understand the binary search . In my submission : If you can find , Then you can use binary search . Binary search actually has one kind Close to The meaning of is in it , Let's first look at a set of codes for the simplest binary search , Take a look at the traditional model of binary search :
int a[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int target = 0;
cin>>target;
int left = 0;
int right = sizeof(a) / sizeof(a[0]) - 1;
while(left <= right)
{
int mid = (left + right) >> 1;
if(a[mid] == target)
{
cout<<mid<<endl;
break;
}
else if(a[mid] < target)
{
left = mid + 1;
}
else
{
right = mid - 1;
}
}Exclude half of the data at a time , until Section Keep approaching the right answer , Find the right answer .
The variation of binary search
The binary search variant here still stays on the basis of traditional binary search , Only slightly modified , The preconditions here are still orderly , Nothing has changed in essence , Be careful , In fact, order is a law , As long as we have laws that can replace order , The premise is that this rule must be able to eliminate half of the data at one time , I will explain one by one later .
seek target >= x The leftmost boundary of the number of
Using the approximation property of binary search , But the difference is that we have found all the binary search this time , Do not give exit halfway , Look at the code first :
Here is a popular solution on the Internet , I will upgrade it later :
int a[] = {1, 2, 2, 2, 3, 4, 5};
int target = 2;// The boundary we are looking for is 2
int left = 0;
int right = sizeof(a) / sizeof(a[0]) - 1;
while(left <= right)
{
int mid = (right + left) / 2;
if(target == a[mid])
{
right = mid - 1;// Do not exit when found , Rather let right Continue to approach , Why right, Because the description is looking for the leftmost boundary of the number
}
else if(target > a[mid])
{
left = mid + 1;
}
else
{
right = mid - 1;
}
}
cout<<left<<endl;// Find boundary , Print or return if it is a function
// perhaps cout<<right + 1<<endl;This is similar to the standard template of binary search , If you want to use [ , ) Of course, it can be changed . The point is how to get the boundary ?
if(target == a[mid])
{
right = mid - 1;// Do not exit when found , Rather let right Continue to approach , Why right, Because the description is looking for the leftmost boundary of the number
}That's the key , When we find the answer, we don't let the binary search stop , But let it keep approaching , Until you find the right answer .
Why in the end left perhaps right + 1 It is the result.
our left and right What does that mean? ?left and right It represents the left and right boundaries of the interval , Why can we use binary search ? The answer is to use the left and right boundaries not only to compress and shrink , Finally, lock to a specific number , It's the same here , Our aim is to find target >= x The leftmost border of , therefore left It's the initiative ,left It's the left border , This left boundary will eventually press target The location of , Why? right Not necessarily the right answer , because right Are passive , As a right boundary, it cannot stand on the position of the left boundary . Here's the picture
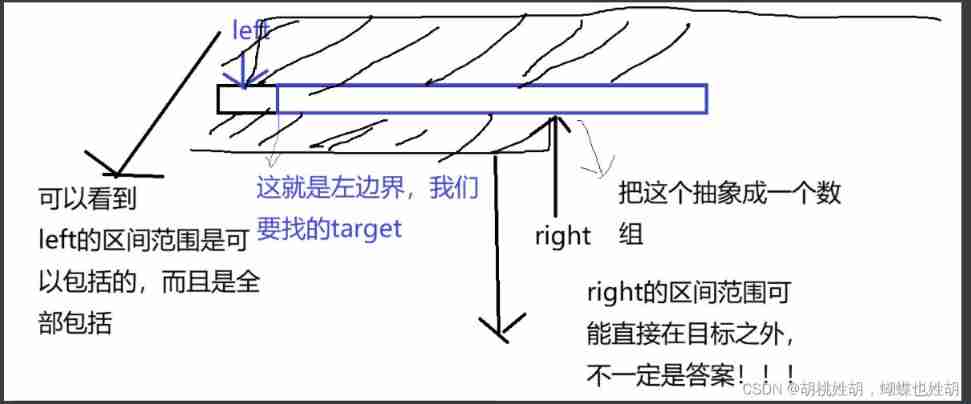
So why right + 1 It can also be the answer ? Because at the end of the cycle left = right + 1, It's that simple .
No return found -1 Do you ?
This is not the same as looking for numbers , Because we let binary search complete , So finally, if there is no boundary we want in our array , Well, it's very likely that left perhaps right Directly outside the scope of the subscript . Therefore, it is necessary to verify before deciding to return left still -1
Check here left Cross border situation of , because left It's the initiative
if(left > sizeof(a) / sizeof(a[0]) || a[left] != target)// The first condition is target Bigger than all , The second is target Smaller than all ,left Still in 0, So just judge 0 Is it what we want .
seek target <= x The rightmost boundary of the number of
Let's put it another way
int a[] = {1, 2, 2, 2, 3, 4, 5};
int target = 2;// The boundary we are looking for is 2
int left = 0;
int right = sizeof(a) / sizeof(a[0]);
while(left < right)
{
if(a[left] == target)
{
left = mid + 1;// Must write mid + 1, The search interval was mentioned earlier ,
}
else if(a[left] < target)
{
left = mid + 1;
}
else
{
right = mid;
}
}
// Check right Cross border situation of
if(right < 0 || a[right] != target)
{
return -1;
}
return right - 1;// Return here right Be right , Because the end condition of the loop is left = right, So back left - 1 It's fine too Why subtract one here ?
Because I have an open section on my right , Final right It must be in the right position in the interval , But because of the open interval , therefore right - 1 It's just target The location of . If you write a closed interval, write it directly right That's all right. .
improvement : We use a variable to hold the boundary value , Finally, return the subscript of the variable , Deal with many situations in this way
int a[] = {1, 2, 2, 2, 3, 4, 5};
int target = 2;// The boundary we are looking for is 2
int left = 0;
int right = sizeof(a) / sizeof(a[0]) - 1;
int temp;// Define temporarily stored variables
while(left <= right)
{
int mid = (right + left) / 2;
if(a[mid] >= target)
{
temp = mid;
right = mid - 1;
}
else
{
left = mid + 1;
}
}
return temp;Application of binary search , Is binary search very rigid ?
34. Find the first and last positions of the elements in the sort array
Model application : Look for a number in the range :
class Solution {
public:
int searchRangeleft(vector<int>& nums, int target)
{
int left = 0;
int right = nums.size() - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] < target)
{
left = mid + 1;
}
else
{
right = mid - 1;
}
}
if(left > nums.size() - 1 || nums[left] != target)
{
return -1;
}
else
{
return left;
}
}
int searchRangeright(vector<int>& nums, int target)
{
int left = 0;
int right = nums.size() - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] > target)
{
right = mid - 1;
}
else
{
left = mid + 1;
}
}
if(right < 0 || nums[right] != target)
{
return -1;
}
else
{
return right;
}
}
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.size() == 0)
{
vector<int> result{-1, -1};
return result;
}
vector<int> result;// Something used to save the results
int lefttemp = searchRangeleft(nums, target);
int righttemp = searchRangeright(nums, target);
result.push_back(lefttemp);
result.push_back(righttemp);
return result;
}
};
There is nothing to explain this problem. In fact . To be exact, it's quite traditional .
Problems can be converted :
class Solution {
public:
int helper(vector<int>& nums, int target)// Here is the right boundary of the search
{
int left = 0;
int right = nums.size() - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] <= target)
{
left = mid + 1;
}
else
{
right = mid - 1;
}
}
return right;
}
int search(vector<int>& nums, int target) {
// Code optimization , Use a function to unify , There's no need to write 2 individual
return helper(nums, target) - helper(nums, target - 1);// Right border and right border - 1
}
};
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
// Problem transformation , Convert to search greater than or equal to target A subscript of , That is greater than or equal to target The boundary of the
int left = 0;
int right = nums.size() - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] >= target)
{
right = mid - 1;
}
else
{
left = mid + 1;
}
}
return left;
}
};
852. The peak index of the mountain array
Mountain array problem , Local maximum problem
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
// Here is exactly the same
int left = 1;
int right = arr.size() - 2;
while(left <= right)// What this means is that we can't start from the beginning and end , This is determined by the definition of the mountain array
{
int mid = (left + right) / 2;
if(arr[mid] >= arr[mid + 1])
{
right = mid - 1;
}
else
{
left = mid + 1;
}
}
return left;
}
};
Local minimum problem
Just find a local minimum in a completely unordered array
Local minimum definition :a[mid - 1] < a[mid] < a[mid + 1], We promise to give a length greater than 3 Array of
int left = 1;
int right = nums.size() - 2;
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] < nums[mid + 1] && nums[mid] < nums[mid - 1])
{
return mid;
}
else
{
if(nums[mid] > nums[mid - 1])
{
left = mid + 1;
}
else
{
right = mid + 1;
}
}
}
Trisection
The trisection method does not divide the interval into three , Instead, veto one-third of each time , Usually used to find the peak , Peak problem
852. The peak index of the mountain array
Usually we use 「 Two points 」 Check the value , You need to ensure that the sequence itself meets 「 Dichotomy 」: When selecting an endpoint ( At baseline ) after , combination 「 A period of satisfaction & Another paragraph is not satisfied 」 To achieve “ Half ” Search results .
seeing the name of a thing one thinks of its function ,「 Three points 」 It is to use two endpoints to divide the interval into three , Then approach the target value by rejecting one-third of the interval each time .
Concrete , Because the peak element is the global maximum , Therefore, we can divide the current interval into l, m1、m1, m2 and m2, r Three paragraph , If meet arr[m1] > arr[m2]arr[m1]>arr[m2], It shows that the peak element cannot exist with m2, r in , Give Way r = m2 - 1r=m2−1 that will do . Another interval analysis is the same .
( The idea comes from : Gongshui Sanye )
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int left = 0;
int right = arr.size() - 1;// It can be written here , because /3 The nature of allows us not to abandon the head and tail
while(left <= right)
{
int third1 = left + (right - left) / 3;
int third2 = right - (right - left) / 3;
if(arr[third1] > arr[third2])
{
right = third2 - 1;
}
else// The implicit condition here is arr[third1] <= arr[third2], Here we can see that we are dominated by the right , So we should return to the right
{
left = third1 + 1;
}
}
return right;
}
};
153. Look for the minimum value in the rotation sort array
Ideas : The array is divided into two segments because of rotation : But we still have Dichotomy , in other words , You can still use binary search to find .
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
if(nums[left] <= nums[right])
{
return nums[0];
}
while(left <= right)
{
if(right - left == 1)
{
return nums[right];
}
int mid = (left + right) / 2;
if(nums[mid] > nums[left])
{
left = mid;// This anti routine writing , Instead, it guarantees left It must not go through ,right Not even
}
else
{
right = mid;
}
}
return -1;
}
};
The depth of the summary :
We have a little time , To jump out of the traditional template , But keep the template in mind , For example, the above question , I don't use templates , And it's written left = mid, and right = mid, This will result in left Never go out of its field ,right Not even , Continuous circulation will eventually lead to a difference between them , And then back again . Using this principle , That is to use left = mid When , We are in a passive State of , We can't escape from any one at this time field , Instead, we can only wait for others to collide with us .
class Solution {
public:
int findMin(vector<int>& nums) {
int low = 0;
int high = nums.size() - 1;
while (low < high) {
int pivot = low + (high - low) / 2;
if (nums[pivot] < nums[high]) {
high = pivot;
}
else {
low = pivot + 1;
}
}
return nums[high];// The end condition of the loop is high = low, So we write high perhaps low It's all possible
}
};
This code is also the code of the above question , But the more this code hides a lot of information .
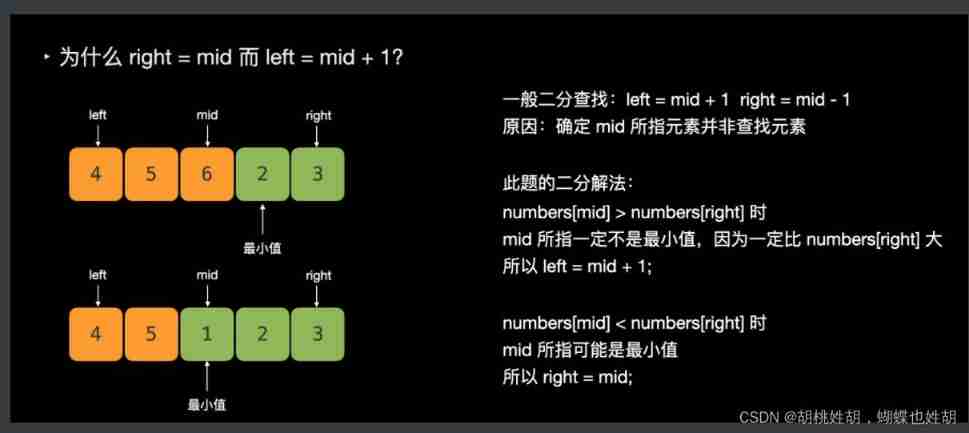
1. We used [ , ], however while Inside <, The purpose is that when we end the cycle low = high Of , And it must be biased towards high The location of , because high = pivot, and if The conditions inside indicate that it will not cross the boundary left over there . This is caused by the nature of this problem .
2. Our comparison needs a standard , It can be high, It can also be low, Why did we choose high?. For this question , This kind of writing is approximate ,while There is no halfway exit in the cycle , The above method doesn't matter , Because there is no exit , So we must not be satisfied while The conditions inside can exit , But this happens to be when the exit conditions are equal , And at this time, the missing element can be obtained from the search interval is the answer itself , But if we don't write low = pivot + 1 Words , We will never get low = high, Because they can't cross their fields , So the following low It must be written like this , It can't be changed , So at this time, we should take high As a standard , The reason is simple , Because in order to high As a standard high Never cross the line , At this time low As a standard, if the time is right low Will run to strange places . therefore high = pivot And with high As a standard, it is a serial condition , Cannot be separated
To make a long story short : We'd better use the right value for comparison , It must be !!! Why high? Again ,4 5 1 2 3, If we use left,nums[pivot] < nums[left], Can you judge which side it is ? All elements on the left must be larger than those on the right , So if you judge that a certain element is better than a certain value on the right , And the value on the right is always smaller on the right , Then this value must also be on the right , If you use the left side to judge , The value on the left , It may also be smaller than the value on the left .
Look again :
class Solution {
public:
int findMin(vector<int>& nums) {
int low = 0;
int high = nums.size() - 1;
while (low <= high) {
int pivot = low + (high - low) / 2;
if (nums[pivot] <= nums[high]) {
high = pivot;
}
else {
low = pivot + 1;
}
}
return nums[high];// The end condition of the loop is high = low, So we write high perhaps low It's all possible
}
};
In the computer world ,÷ An integer is going to the small side .
This code will Dead cycle .
[3,4,5,1,2], Because when we low = high When , The cycle is not over yet , At this time pivot It must still be where it is , Then it happens again high = pivot, Keep cycling , Cannot break the balance . What's the problem ? if (nums[pivot] <= nums[high]). Because of this = and high = pivot This passive state overlaps , So this happens , Here we also get some enlightenment , That's it When your cycle condition is low == high It's not over yet , If you write a passive state below , Then the condition of this passive state must not be =.
Let's get rid of this =,
class Solution {
public:
int findMin(vector<int>& nums) {
int low = 0;
int high = nums.size() - 1;
while (low <= high) {
int pivot = low + (high - low) / 2;
if (nums[pivot] < nums[high]) {
high = pivot;
}
else {
low = pivot + 1;
}
}
return nums[high];// The end condition of the loop is high = low, So we write high perhaps low It's all possible
}
};
You can find oj After that .return nums[low - 1] It's fine too , We can look at it in two ways :1. The end condition of the loop 2. If you want to end stiffness in the same state , Can only be low = pivot + 1, conversely , If you write the conditions , If you can't reach this key node , Then there must be problems . Then if we change while There will be no dead cycle if there are conditions inside :
class Solution {
public:
int findMin(vector<int>& nums) {
int low = 0;
int high = nums.size() - 1;
while (low < high) {
int pivot = low + (high - low) / 2;
if (nums[pivot] < nums[high]) {// This is the time , You can add an equal sign here or not high = pivot;
}
else {
low = pivot + 1;
}
}
return nums[high];// The end condition of the loop is high = low, So we write high perhaps low It's all possible
}
};
( Images from leetcode Official explanation )
About while Add the equals sign in the brackets of , My suggestion is not to add , Because after adding it, you have a greater possibility of causing a dead cycle , So don't wait , One of the missing answers in this question is the answer , That's all right. . The explanation we made earlier is just to make the topic more profound .
The difficulty increases again :
154. Look for the minimum value in the rotation sort array II
The difference between this question and the previous one is : Repetition is allowed here , In fact, we only need to add a small piece of code on the original basis
class Solution {
public:
int findMin(vector<int>& nums) {
// This method does not need to be considered as much as above , Because we have conditions that can be judged inside the loop
int left = 0;
int right = nums.size() - 1;
if(nums.size() == 1)// It must be judged here , Because it can't be written below =
{
return nums[0];
}
if(nums[left] < nums[right])// You can't write here =[3, 1, 3]
{
return nums[left];
}
while(left <= right)
{
if(right - left == 1)
{
return nums[right];
}
int mid = (left + right) / 2;
if(nums[mid] == nums[left] && nums[left] == nums[right])// It shows that we cannot make a good judgment , At this time, take a linear approach
{
int result = nums[left];
for(int i = left + 1; i < right; ++i)// Here we no longer need to judge left and right The location of
{
if(nums[i] < result)
{
return nums[i];
}
}
}
if(nums[mid] >= nums[left])
{
left = mid;
}
else
{
right = mid;
}
}
return -1;
}
};
The overall framework of the topic is the same as before , There is no essential change
Or so :
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
while(left < right)
{
int mid = (left + right) / 2;
if(nums[mid] < nums[right])
{
right = mid;
}
else if(nums[mid] > nums[right])
{
left = mid + 1;
}
else
{
right--;// Reduce the scale of the problem
}
}
return nums[left];
}
};
To be continued .....
边栏推荐
- NFT on fingertips | evaluate ambire on G2, and have the opportunity to obtain limited edition collections
- Leetcode 78: subset
- Path analysis model
- OpenJudge NOI 2.1 1661:Bomb Game
- CDN acceleration and cracking anti-theft chain function
- Uncaught typeerror: cannot red properties of undefined (reading 'beforeeach') solution
- The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
- Yield method of tread
- Crawling exercise: Notice of crawling Henan Agricultural University
- word中把带有某个符号的行全部选中,更改为标题
猜你喜欢
Oracle column to row -- a field is converted to multiple rows according to the specified separator
呆错图床系统源码图片CDN加速与破解防盗链功能

【MySQL学习笔记32】mvcc
You deserve this high-value open-source third-party Netease cloud music player
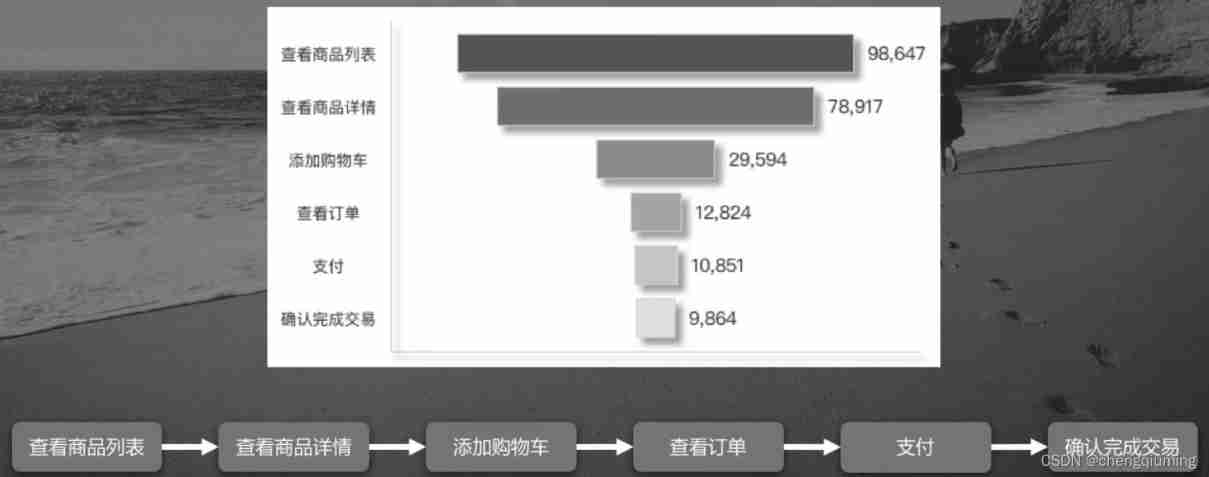
Path analysis model

The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
微信脑力比拼答题小程序_支持流量主带最新题库文件
首发织梦百度推送插件全自动收录优化seo收录模块

Oracle database 11gr2 uses TDE transparent data encryption to report an error ora28353. If you run to close the wallet, you will report an error ora28365. If you run to open the wallet, you will repor

学go之路(一)go的基本介绍到第一个helloworld
随机推荐
[MySQL learning notes 32] mvcc
word怎么只删除英语保留汉语或删除汉语保留英文
The best way to learn SEO: search engine
TypeScript接口与泛型的使用
Openjudge noi 2.1 1749: Digital Square
[MySQL learning notes 30] lock (non tutorial)
Oracle column to row -- a field is converted to multiple rows according to the specified separator
ORACLE列转行--某字段按指定分隔符转多行
CDN acceleration and cracking anti-theft chain function
微信脑力比拼答题小程序_支持流量主带最新题库文件
LeetCode Algorithm 2181. Merge nodes between zero
The psychological process from autojs to ice fox intelligent assistance
word设置目录
“无聊猿” BAYC 的内忧与外患
Solution to the problem of breakthrough in OWASP juice shop shooting range
If Jerry's Bluetooth device wants to send data to the mobile phone, the mobile phone needs to open the notify channel first [article]
How MySQL merges data
Twelve rules for naming variables
OpenJudge NOI 2.1 1661:Bomb Game
Typescript function definition