当前位置:网站首页>P4147 "jade toad Palace"
P4147 "jade toad Palace"
2022-06-11 09:35:00 【hotarugali】
1. subject
Topic link :P4147「 Jade toad Palace 」 .
Background
one day , kitten rainbow and freda Came to Tianmen Mountain Jade toad palace in Zhangjiajie, Western Hunan , Blue rabbit, the leader of Yuchan palace, entertained them , And give them a piece of land .
Title Description
The land is divided into N\times M Lattice , In each cell, it says R perhaps F,R On behalf of this land has been given rainbow,F On behalf of this land has been given freda.
Now? freda To sell cute here ... It's looking for a rectangular piece of land , Ask that the land be marked with F And the largest area .
however rainbow and freda Of OI The level is weak , I can't find the land , And the blue rabbit wants to see freda Adorable ( She obviously can't program ……), So they decided , If you find land area is S, They're all for you S Two silver .
Input format
The first line has two integers N,M, It means that the rectangular land has N That's ok M Column .
Next N That's ok , Each row M Characters separated by spaces F or R, Describes rectangular land .
Output format
Output an integer , How much money can you get , namely 「3× Maximum F Rectangular land area 」 Value .
I/o sample
Input #1
5 6 R F F F F F F F F F F F R R R F F F F F F F F F F F F F F F
Output #1
45
explain / Tips
about 50\% The data of ,1\leq N,M\leq 200.
about 100\% The data of ,1\leq N,M\leq 1000.
2. Answer key
analysis
The typical problem of finding the sum of maximal submatrix , That is to ask for a M \times N Moment The maximum value of the sum of the elements of a submatrix in a matrix . This can be solved with a monotone stack . For each column element in each row , Count up continuous F The number of , That is, a bar chart based on each behavior , Each column corresponds to a bar rectangle , The width of the rectangle is 111 , High means that the element is continuously calculated upwards F The number of , This is the typical problem of calculating the maximum inner rectangular area of a rectangular statistical graph , use O(N) A perfect solution to the monotonous stack . Because of N That's ok , Each row constructs a rectangular statistical graph , Therefore, the total complexity is O(N^2).
Code
#include <bits/stdc++.h>
#define ll int
#define MAXN 1005
using namespace std;
// Rectangular statistical chart
struct RC {
ll i;
ll v;
RC():i(0), v(0) {}
RC(ll _i, ll _v): i(_i), v(_v) {}
};
// Calculate the maximum submatrix area
ll maxRectangle(ll *A, ll n) {
ll ans = 0;
ll depth = 0;
RC stack[MAXN];
stack[depth] = RC(-1,-1);
for(ll i = 0; i < n; ++i) {
RC t(i,A[i]);
ll sdepth = depth;
while(depth && stack[depth].v >= A[i]) {
ans = max(ans, (stack[sdepth].i-stack[depth-1].i)*stack[depth].v);
--depth;
}
stack[++depth] = t;
}
ll sdepth = depth;
while(depth) {
ans = max(ans, (stack[sdepth].i-stack[depth-1].i)*stack[depth].v);
--depth;
}
return ans;
}
int main()
{
ll n, m;
ll a[MAXN][MAXN], b[MAXN][MAXN];
scanf("%d%d", &n, &m);
for(ll i = 0; i < n; ++i) {
for(ll j = 0; j < m; ++j) {
char str[2];
scanf("%s", str);
if(str[0] == 'R') {
a[i][j] = 0;
} else {
a[i][j] = 1;
}
}
}
for(ll j = 0; j < m; ++j) b[0][j] = a[0][j];
for(ll i = 1; i < n; ++i) {
for(ll j = 0; j < m; ++j) {
if(a[i][j]) {
b[i][j] = b[i-1][j] + 1;
} else {
b[i][j] = 0;
}
}
}
ll ans = 0;
for(ll i = 0; i < n; ++i) {
ans = max(ans, maxRectangle(b[i], m));
}
printf("%d\n", 3*ans);
return 0;
}边栏推荐
猜你喜欢

Exclusive interview - dialogue on open source Zhai Jia: excellent open source projects should be seen by more people. I am honored to participate in them

Type-C蓝牙音箱单口可充可OTG方案

报错RuntimeError: BlobReader error: The version of imported blob doesn‘t match graph_transformer

Openstack explanation (24) -- registration of neutron service
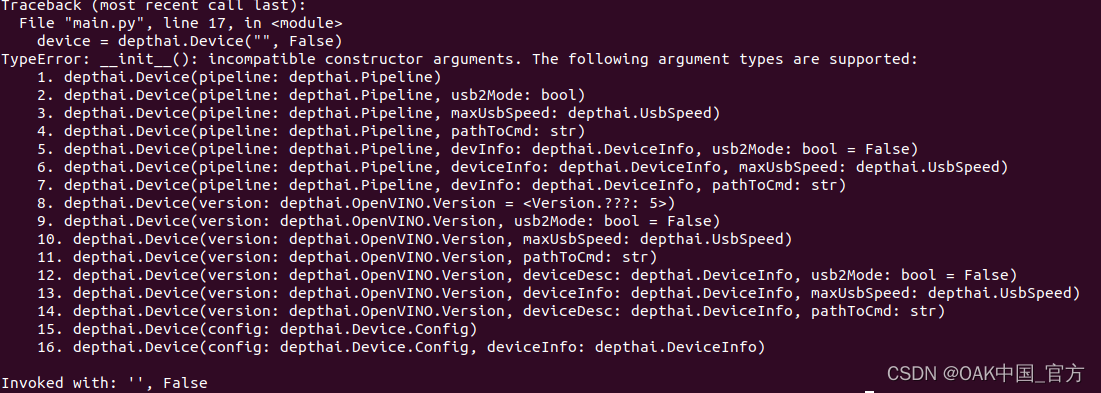
报错device = depthai.Device(““, False) TypeError: _init_(): incompatible constructor arguments.

Pulsar job Plaza | Tencent, Huawei cloud, shrimp skin, Zhong'an insurance, streamnational and other hot jobs
Machine learning notes - in depth Learning Skills Checklist

报错Output image is bigger(1228800B) than maximum frame size specified in properties(1048576B)

Technical practice of dolphin dispatching in kubernetes system

Type-C扩展坞自适应供电专利维权案例
随机推荐
Before applying data warehouse ODBC, you need to understand these problems first
考研数学 【数列极限证明题】题型方法总结
Thread theory
Set up redis highly available cluster environment
Ecological co construction | 2021 streamnational excellent partner of the year comes out!
Modularnotfounderror: no module named 'find_ version’
Sed explanation of shell script (SED command, sed -e, sed s/ new / old /...)
What is WSGI?
PCBA方案定制,开发腕式血压计方案
Where is it safer to open an account for soda ash futures? How much do you need to buy at least?
Don't use redis list to implement message queue. Stream is designed for queues
报错ModularNotFoundError: No module named ‘find_version’
Remote office related issues to be considered by enterprises
OpenCV OAK-D-W广角相机测试
2161. 根据给定数字划分数组
企业需要考虑的远程办公相关问题
A summary of the problem type and method for proving the limit of sequence in postgraduate entrance examination
基于SIC32F911RET6设计的腕式血压计方案
[FAQ for novices on the road] about data visualization
[TiO websocket] v. TiO websocket server counts the number of online people