13.＜ tag-动态规划和回文字串＞lt.647. 回文子串 + lt.516.最长回文子序列

lt.647. 回文子串

[案例需求]

[思路分析一, 暴力解法]

[代码实现]

[思路分析二, 动态规划]

1. 确定dp数组以及下标的含义
   boolean dp[i][j]: 表示区间范围为[i, j] (注意事项左闭右闭)的字串是否是回文字串, 如果dp[i][j]为true, 否则为false;

2. 确定递推公式
   整体上是两种, 就是s[i]与s[j]相等, s[i]和s[j]不相等这两种.

1. 当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。
2. 下标i 与 j相差为1，例如aa，也是回文子串
3. 下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

• 递推公式如下

if (s[i] == s[j]) {
    
    if (j - i <= 1) {
     // 情况一 和 情况二
        result++;
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) {
     // 情况三
        result++;
        dp[i][j] = true;
    }
}

• result就是统计回文子串的数量。
• 注意这里我没有列出当s[i]与s[j]不相等的时候，因为在下面dp[i][j]初始化的时候，就初始为false。

3. dp数组初始化
   dp[i][j]可以初始化为true么？ 当然不行，怎能刚开始就全都匹配上了。所以dp[i][j]初始化为false。

4. 确定遍历顺序
   

for (int i = s.size() - 1; i >= 0; i--) {
      // 注意遍历顺序
    for (int j = i; j < s.size(); j++) {
    
        if (s[i] == s[j]) {
    
            if (j - i <= 1) {
     // 情况一 和 情况二
                result++;
                dp[i][j] = true;
            } else if (dp[i + 1][j - 1]) {
     // 情况三
                result++;
                dp[i][j] = true;
            }
        }
    }
}

5. 举例推导

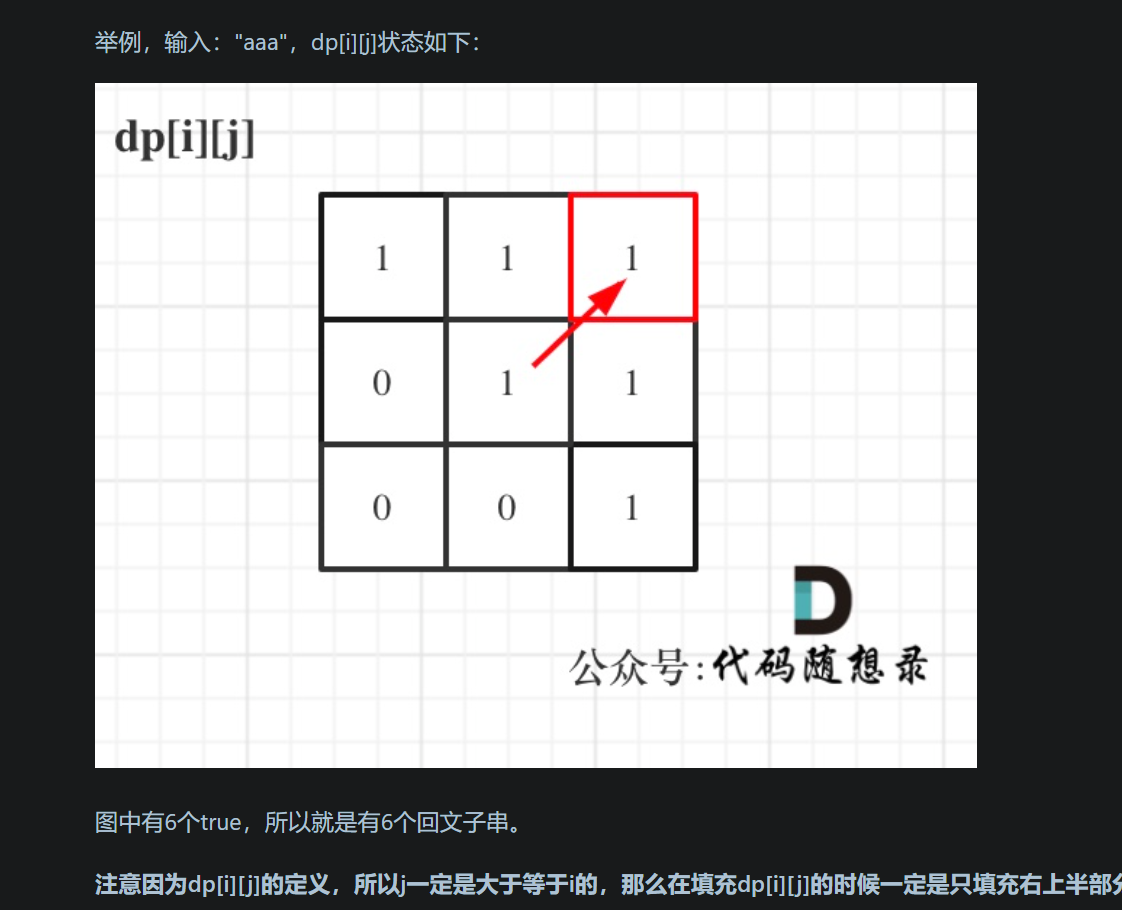
[代码实现]

class Solution {
    
    public int countSubstrings(String s) {
    
        int len, ans = 0;
        if (s == null || (len = s.length()) < 1) return 0;
        //dp[i][j]：s字符串下标i到下标j的字串是否是一个回文串，即s[i, j]
        boolean[][] dp = new boolean[len][len];
        for (int j = 0; j < len; j++) {
    
            for (int i = 0; i <= j; i++) {
    
                //当两端字母一样时，才可以两端收缩进一步判断
                if (s.charAt(i) == s.charAt(j)) {
    
                    //i++，j--，即两端收缩之后i,j指针指向同一个字符或者i超过j了,必然是一个回文串
                    if (j - i < 3) {
    
                        dp[i][j] = true;
                    } else {
    
                        //否则通过收缩之后的字串判断
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                } else {
    //两端字符不一样，不是回文串
                    dp[i][j] = false;
                }
            }
        }
        //遍历每一个字串，统计回文串个数
        for (int i = 0; i < len; i++) {
    
            for (int j = 0; j < len; j++) {
    
                if (dp[i][j]) ans++;
            }
        }
        return ans;
    }
}

lt.516.最长回文子序列

[案例需求]

[思路分析]

[代码实现]

public class Solution {
    
    public int longestPalindromeSubseq(String s) {
    
        int len = s.length();
        int[][] dp = new int[len + 1][len + 1];
        for (int i = len - 1; i >= 0; i--) {
     // 从后往前遍历 保证情况不漏
            dp[i][i] = 1; // 初始化
            for (int j = i + 1; j < len; j++) {
    
                if (s.charAt(i) == s.charAt(j)) {
    
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
    
                    dp[i][j] = Math.max(dp[i + 1][j], Math.max(dp[i][j], dp[i][j - 1]));
                }
            }
        }
        return dp[0][len - 1];
    }
}