当前位置:网站首页>唤醒手腕 - 神经网络与深度学习(Tensorflow应用)更新中
唤醒手腕 - 神经网络与深度学习(Tensorflow应用)更新中
2022-06-11 23:00:00 【唤醒手腕】
机器学习、深度学习简介
现在搞传统机器学习相关的研究论文确实占比不太高,有的人吐槽深度学习就是个系统工程而已,没有数学含金量。但是无可否认的是深度学习是在太好用啦,极大地简化了传统机器学习的整体算法分析和学习流程,更重要的是在一些通用的领域任务刷新了传统机器学习算法达不到的精度和准确率。
深度学习这几年特别火,就像几年前的大数据一样,不过深度学习其主要还是属于机器学习的范畴领域内,所以这篇文章里面我们来唠一唠机器学习和深度学习的算法流程区别。

机器学习是什么?
简单说就是无序数据转化为价值的方法,从广义上来说,机器学习是一种能够赋予机器学习的能力以此让它完成直接编程无法完成的功能的方法。但从实践的意义上来说,机器学习是一种通过利用数据,训练出模型,然后使用模型预测的一种方法。
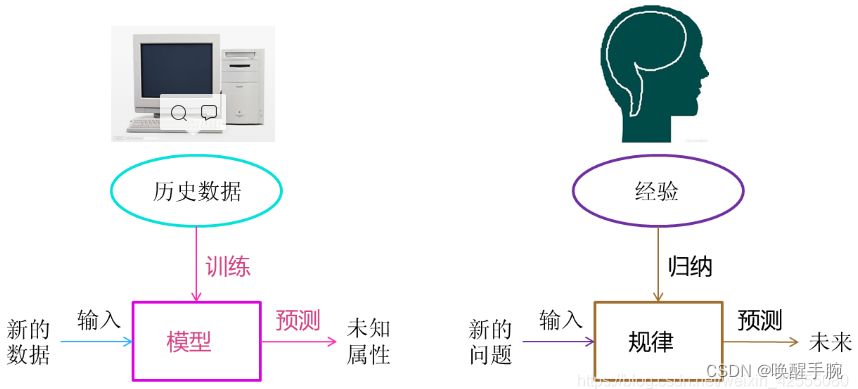
- “训练”与“预测”是机器学习的两个过程,“模型”则是过程的中间输出结果,“训练”产生“模型”,“模型”指导 “预测”。
- 机器学习方法是计算机利用已有的数据(经验),得出了某种模型(迟到的规律),并利用此模型预测未来(是否迟到)的一种方法。
- 让我们把机器学习的过程与人类对历史经验归纳的过程做个比对。
机器学习价值和重要性?
我们专注于这些工具解决实际问题的能力和机器学习实践,从数据中抽取规律,并用来预测未来。
自动化 (Automatically) : 机器学习方法可以看做是自动化生成算法的算法。
快速 (Fast) :机器学习方法可以节约时间。相比如人工处理,机器学习方法可以更加快速分析样例数据并生成算法。
精确性 (Accurate) : 由于自动化的特性,机器学习方法可以基于更多的数据、运行更长的时间,生成更精确的决策。
规模 (Scale) : 机器学习方法可以给人工无法解决的问题提供解决方案。
机器学习应用举例
分类问题:图像识别、垃圾邮件识别
回归问题:股价预测、房价预测
排序问题:点击率预估、推荐
生成问题:图像生成、图像风格转换、图像文字描述生成
机器学习应用流程
机器学习的算法流程
实际上机器学习研究的就是数据科学(听上去有点无聊),下面是机器学习算法的主要流程:主要从1)数据集准备、2)探索性的对数据进行分析、3)数据预处理、4)数据分割、5)机器学习算法建模、6)选择机器学习任务,当然到最后就是评价机器学习算法对实际数据的应用情况如何。
深度学习算法集合
包含:1. 卷积神经网络 2. 循环神经网络 3. 自动编码器 4. 稀疏编码 5. 深度信念网络 6.限制玻尔兹曼机
神经元 - 逻辑斯蒂回归模型
由于神经网络的模拟对象是人的大脑,那么在讨论具体的模型之前,我们有必要先从生物学的角度来看看人的大脑有哪些特性。
根据生物学的研究,人脑的计算单元是神经元(neuron)。它能根据环境变化做出反应,再将信息给其他的神经元。在人脑中,大约有 860 亿个神经元,它们相互联结构成了极其复杂的神经系统,而后者正是人类智慧的物质基础。因此遵循人脑的生物结构,我们首先需要搭建模型来模拟人的神经元。
神经元基本介绍
神经元是神经网络的最小结构,将多个神经元组合在一起就形成了神经网络。神经元也可以经过一些设置之后形成一个逻辑回归模型。

输入信号来自外部或别的处理单元的输出,在数学上表示为行向量 x = ( x 1 , x 2 , … , x m ) x=(x_1,x_2,…,x_m) x=(x1,x2,…,xm),其中 x i x_i xi 为第 i i i 个输入的激励电平, m m m 表示输入数目。
连接到结点k的加权表示为加权向量 W k = ( w k 1 , w k 2 , … , w k m ) W_k=(w_k1,w_k2,…,w_km) Wk=(wk1,wk2,…,wkm),其中 w k i w_{ki} wki 表示从结点 i i i(或第 i i i 个输入点)到结点 k k k 的加权,或称 i i i 与 k k k 结点之间的连接强度。
计算功能的主要作用是对每个输入信号进行处理以确定其强度(加权);确定所有输入信号的组合效果(求和);然后确定其输出(转移特性)。
也就是说,当神经元接受来自 n 个其他神经元传递过来的输入信号,神经元将接受到的输入值按照某种权重加起来,叠加起来的刺激强度 S 可用公式表示:
S = w 1 x 1 + w 2 x 2 + ⋯ + w n x n = ∑ i = 1 n w i x i S = w_1x_1 + w_2x_2 + \cdots + w_nx_n = \sum_{i=1}^{n}{w_ix_i} S=w1x1+w2x2+⋯+wnxn=i=1∑nwixi
而这种输出,并非赤裸裸地直接输出,而是与当前神经元的阈值进行比较,然后通过激活函数(Activation Function)向外表达输出,在概念上这叫做感知机(Perceptron),其模型可用公式表示:
y = f ( ∑ i = 1 n w i x i − θ ) y = f(\sum_{i=1}^{n}{w_ix_i - \theta}) y=f(i=1∑nwixi−θ)
在这里的 θ \theta θ 就是所谓的阈值
(Threshold), f f f 就是激活函数, y y y 就是最终输出。
神经元目标
神经元的目标是根据大量输入和输出示例调整权重。因此,假设我们向神经元展示了一千个猫的图片和非猫图片的示例,并且我们展示了每个示例中我们展示了哪些特征以及我们确信它们在这里的确定程度。基于上千张图像神经元决定:
哪些特征是重要的和正面的(例如每只猫的都有一条尾巴,因此权重必须大而且是正的)
哪些特征并不重要(例如,只有少数图片有2只眼睛,因此权重很小)
哪些特征是重要的和负面的(例如每个包含角的图片实际上是一只独角兽而不是猫的图片,所以权重必须大而且是负的)
神经元 - 简单基本计算问题
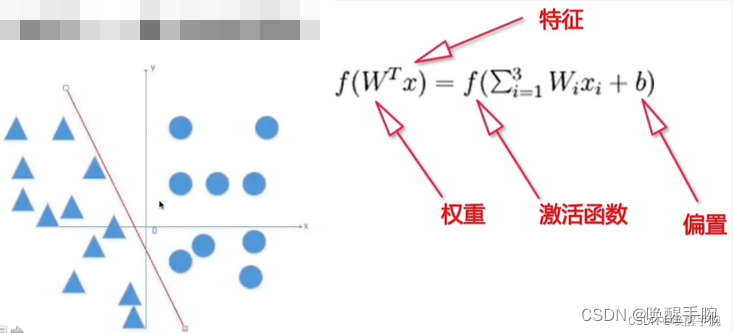
神经网络是一组按层次组成的神经元。每个神经元都是一个数学运算,它接受输入,乘以它的权重,然后通过激活函数将总和传递给其他神经元。神经网络正在学习如何根据前面的例子调整输入的权重来对输入进行分类。
它把输入值乘以它们的权重,然后将它们相加起来,之后,它将激活函数应用于求和。

二分类的逻辑斯谛模型
逻辑斯谛分布的分布函数 F ( x ) F(x) F(x) 的曲线如图所示,其图形是一条S形曲线,曲线在中心附近增长最快,在两端增长速度较慢。当 x x x 无穷大时, F ( x ) F(x) F(x) 接近于 1;当 x x x 无穷小时, F ( x ) F(x) F(x)接近于 0。
二项逻辑斯蒂回归模型是一种分类模型,由条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X) 表示,形式为参数化的逻辑斯蒂分布?这里随机变量X取值为实数,随机变量 Y Y Y 取值为 1 或 0。

假设一组数据的分布如上图所示,建立一个什么样的模型将两个类别区分开来呢?
线性回归模型 z = W T x + b z = W^Tx + b z=WTx+b,线性回归模型的输出值是一个实值,而二分类任务的输出标记(在二项逻辑斯蒂回归中,我们强制将正类标记为1,负类标记为0,后面将会提到这样做的原因),于是我们考虑将实值 z z z 转换为 0 / 1 0/1 0/1 值。
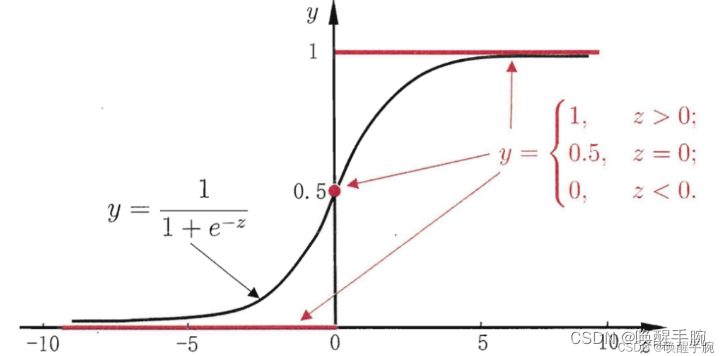
最 理 想 的 单 位 阶 跃 函 数 : y = { 0 i f z < 0 0.5 i f z = 0 1 i f z > 0 最理想的单位阶跃函数: y = \begin{cases} 0 & if & z < 0 \\ 0.5 & if & z=0 \\ 1 & if & z > 0\end{cases} 最理想的单位阶跃函数:y=⎩⎪⎨⎪⎧00.51ifififz<0z=0z>0
但单位阶跃函数是不连续的,我们希望找到在一定程度上接近单位阶跃函数的替代函数,并希望它单调可微,对数几率函数正是这样一个常用的替代函数,对数几率函数(又叫sigmod函数,logistic函数)
y = 1 1 + e − z y = \frac{1}{1+e^{-z}} y=1+e−z1
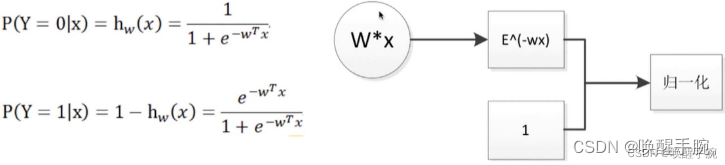
对于给定的输入实例 x x x,按照上述分布函数可以求得 P ( Y = 1 ∣ x ) 和 P ( Y = 0 ∣ x ) P(Y=1|x)和P(Y=0|x) P(Y=1∣x)和P(Y=0∣x) 。逻辑斯谛回归是比较两个条件概率值的大小,将实例 x x x 分到概率值大的那一类。
神经元多输出: W W W 从向量扩展为矩阵,输出 W ∗ x W*x W∗x 则变成向量
在统计学里,多类别逻辑回归是一个将逻辑回归一般化成多类别问题得到的分类方法。用更加专业的话来说,它就是一个用来预测一个具有类别分布的因变量不同可能结果的概率的模型。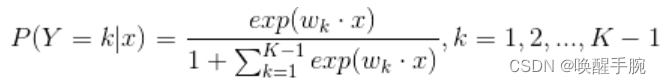
二项逻辑斯谛回归模型是二项分类模型,用于二分类问题中。可以将其推广到多项逻辑斯谛回归模型,用于多分类问题。假设离散型随机变量Y的可能取值集合是{1,2,…,K},那么多项逻辑斯谛回归模型是:

多项逻辑斯蒂回归又称为softmax回归,是二项逻辑斯蒂回归的推广,用于多类别分类。
梯度下降、损失函数
什么是梯度下降?
首先我们可以把梯度下降拆解为梯度+下降,那么梯度可以理解为导数(对于多维可以理解为偏导),那么合起来变成了:导数下降,那问题来了,导数下降是干什么的?这里我直接给出答案:梯度下降就是用来求某个函数最小值时自变量对应取值。
其中这句话中的某个函数是指:损失函数(cost/loss function),直接点就是误差函数。
损失函数就是一个自变量为算法的参数,函数值为误差值的函数。所以梯度下降就是找让误差值最小时候算法取的参数。
在机器学习中有一类算法就是产生一条曲线来拟合现有的数据,这样子就可以实现预测未来的数据,我们将这个算法叫做回归。
还有一类算法也是产生一条曲线,但是这条曲线用来将点分为两块,实现分类,我们将这个算法叫做分类。但是这面两种算法产生的拟合曲线并不是完全和现有的点重合,拟合曲线和真实值之间有一个误差。所以我们一般用损失函数的值来衡量这个误差,所以损失函数的误差值越小说明拟合效果越好。
简单理解:损失函数表示预测值与实际值之间的误差。
声明式编程介绍

越是声明式,意味着下层要做更多的东西,或者说能力越强。也意味着效率的损失。越是命令式,意味着上层对下层有更多的操作空间,可以按照自己特定的需求要求下层按照某种方式来处理。
实际上,这对概念应该叫做“声明式接口”和“命令式接口”。可能是因为它大部分时候是在谈论“语言”这种接口方式时才会用到,所以会叫做“声明式编程”和“命令式编程”。
当然,你也可以把它当成一种编程思想,也就是说,在构建自己的代码时,为了结构的清晰可读,把代码分层,层之间的接口尽量声明式。这样你的代码自然在一层上主要描述从人的角度需要什么;另一层上用计算机逻辑实现人的需要。

数据处理与模型图构建
TensorFlow是学习深度学习时常用的Python神经网络框架。TensorFlow 是一个采用数据流图(data flow graphs),用于数值计算的开源软件库。
TensorFlow 最初由Google大脑小组(隶属于Google机器智能研究机构)的研究员和工程师们开发出来,用于机器学习和深度神经网络方面的研究,但这个系统的通用性使其也可广泛用于其他计算领域。
它是谷歌基于DistBelief进行研发的第二代人工智能学习系统。2015年11月9日,Google发布人工智能系统TensorFlow并宣布开源。
.借助 Anaconda 进行安装 tensorflow
Anaconda官方网站:https://www.anaconda.com/
选择相应的Anaconda进行安装,进入Anaconda的官网,下载对应系统版本的Anaconda,官网现在的版本是 For Windows Python 3.9 • 64-Bit Graphical Installer • 594 MB。
就和安装普通的软件一样,全部选择默认即可,注意勾选将 python3.9 添加进环境变量。
anaconda配置:打开cmd切换到国内的镜像源
conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/
conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/main/
TensorFlow安装:这里建议安装tensorflow 1.15 的版本,需要安装其他版本的只需要在安装tensorflow的命令行中修改对应版本号即可。
打开cmd运行,首先创造 tensorflow 1.15 需要的环境(cmd 命令行 python -V 查看版本)
conda create -n tensorflow pip python=3.9
然后进行激活TensorFlow环境
activate tensorflow
边栏推荐
- Analysis on the market prospect of smart home based on ZigBee protocol wireless module
- Research Report on development trend and competitive strategy of global metallized high barrier film industry
- How to make scripts executable anywhere
- IEEE-754 floating point converter
- 2022 online summit of emerging market brands going to sea will be held soon advance AI CEO Shou Dong will be invited to attend
- Inventory | more than 20 typical security incidents occurred in February, with a loss of nearly $400million
- [Day2 intensive literature reading] time in the mind: using space to think about time
- 华为设备配置HoVPN
- Only three steps are needed to learn how to use low code thingjs to connect with Sen data Dix data
- Processus postgresql10
猜你喜欢

How to do investment analysis in the real estate industry? This article tells you
![[Day8 literature extensive reading] space and time in the child's mind: evidence for a cross dimensional symmetry](/img/c2/e70e7c32c5dc5554dea29cb4627644.png)
[Day8 literature extensive reading] space and time in the child's mind: evidence for a cross dimensional symmetry
![[day15 literature extensive reading] numerical magnetic effects temporary memories but not time encoding](/img/57/9ce851636b927813a55faedb4ecd48.png)
[day15 literature extensive reading] numerical magnetic effects temporary memories but not time encoding

Wireless communication comparison of si4463, si4438 and Si4432 schemes of wireless data transmission module

Lekao.com: what is the difference between Level 3 health managers and level 2 health managers?

The second bullet of in-depth dialogue with the container service ack distribution: how to build a hybrid cloud unified network plane with the help of hybridnet
想做钢铁侠?听说很多大佬都是用它入门的

Is it too troublesome to turn pages manually when you encounter a form? I'll teach you to write a script that shows all the data on one page

A method of relay for ultra long distance wireless transmission of low power wireless module

【Day8 文献泛读】Space and Time in the Child‘s Mind: Evidence for a Cross-Dimensional Asymmetry
随机推荐
H.265编码原理入门
Lekao.com: what is the difference between Level 3 health managers and level 2 health managers?
Read dense visual slam for rgb-d cameras
习题11-3 计算最长的字符串长度 (15 分)
Gcache of goframe memory cache
Small program startup performance optimization practice
2022新兴市场品牌出海线上峰会即将举办 ADVANCE.AI CEO寿栋将受邀出席
【Day15 文献泛读】Numerical magnitude affects temporal memories but not time encoding
IEEE-754 浮点转换器
【自然语言处理】【多模态】ALBEF:基于动量蒸馏的视觉语言表示学习
习题11-2 查找星期 (15 分)
2022年安全员-B证理论题库及模拟考试
IEEE浮点数尾数向偶舍入-四舍六入五成双
Point cloud read / write (2): read / write TXT point cloud (space separated | comma separated)
Google搜索為什麼不能無限分頁?
Here we go! Dragon lizard community enters PKU classroom
动态规划之0-1背包问题(详解+分析+原码)
[technology sharing] after 16 years, how to successfully implement the dual active traffic architecture of zhubajie.com
[day15 literature extensive reading] numerical magnetic effects temporary memories but not time encoding
关于腾讯域名解析阿里云服务器的一些坑