[point cloud processing paper crazy reading frontier version 10] - mvtn: multi view transformation network for 3D shape recognition

Abstract

• problem ： Among many point cloud processing methods ,Multi-view projection The perspective of methods is often set heuristically or the same for all shapes .
• Method ： Put forward a method , Learn how to better set these perspectives .
• details ： Introduced Multi-View Transformation Network (MVTN), Used to find for 3D The best angle of view for shape recognition , The design of the whole network is derivable .MVTN It can be trained end-to-end , And use it with any multi perspective network for 3D Shape recognition . This article will MVTN Integrate with a new adaptive multi perspective network , The network can not only handle 3D mesh, You can also handle point clouds .
• Code ：https://github.com/ajhamdi/MVTN Pytorch edition

Related work

• MVTN Learn the spatial transformation of input data , No extra supervision is used in the learning process , Nor adjust the learning process .

Method

Overview of Multi-View 3D Recognition

The training of multi view network can be expressed as ：
$$\begin{array}{rl}& \underset{{\mathbf{\theta }}_{\mathbf{C}}}{\mathrm{argmin}}\sum _n^{N}L\left(\mathbf{C}\left({\mathbf{X}}_n\right),y_n\right)\\ =& \underset{{\mathbf{\theta }}_{\mathbf{C}}}{\mathrm{argmin}}\sum _n^{N}L\left(\mathbf{C}\left(\mathbf{R}\left({\mathbf{S}}_n,{\mathbf{u}}_0\right)\right),y_n\right)\end{array}$$
among $L$ Is the loss function of a specific task ,$N$ It's a dataset 3D Number of shapes ,$y_n$ It's No $n$ individual 3D shape ${\mathbf{S}}_n$ Of label.${\mathbf{u}}_0\in {\mathbb{R}}^{\tau }$ Of the entire dataset $\tau$ Set of scene parameters , These parameters represent the properties that affect the rendered image , Including viewpoint 、 The light 、 Color and background .$\mathbf{R}$ It's the renderer , In shape ${\mathbf{S}}_n$ And parameters ${\mathbf{u}}_0$ As input , Get each shape $M$ Multiple view images ${\mathbf{X}}_n$. stay MVCNN in ,$\mathbf{C}=\mathrm{MLP}\left({\max }_i\mathbf{f}\left({\mathbf{x}}_i\right)\right)$,$\mathbf{f}:{\mathbb{R}}^{h\times w\times c}\to {\mathbb{R}}^d$ It's a 2D CNN backbone; stay ViewGCN in ,$\mathbf{C}=\mathrm{MLP}(cat{}_{\mathrm{G}\mathrm{C}\mathrm{N}}\left(\mathbf{f}\left({\mathbf{x}}_i\right)\right))$,$ca{t}_{\mathrm{G}\mathrm{C}\mathrm{N}}$ It is the aggregation of view features learned from graph convolution network .${\mathbf{\theta }}_{\mathbf{C}}$ It's a multi view network $\mathbf{C}$ Parameters of . In the experimental part , Scene parameters $\mathbf{u}$ Expressed as the camera angle pointing to the center of the target azimuth (azimuth) Elevation angle (elevation) angles, therefore $\tau =2M$

Multi-View Transformation Network (MVTN)

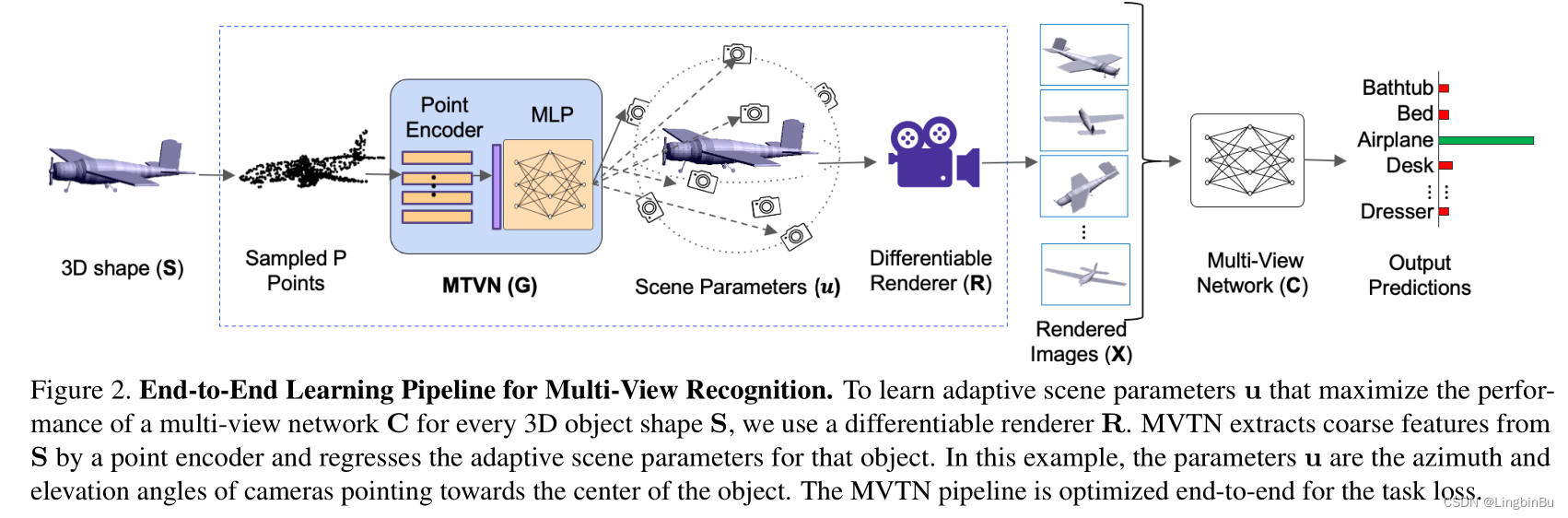
Previous multi view methods are based on images $\mathbf{X}$ As 3D Unique representation of shape , among $\mathbf{X}$ Is to use fixed scene parameters ${\mathbf{u}}_0$ Got . contrary , This paper considers a more general case , take $\mathbf{u}$ Set the boundary to $\pm {\mathbf{u}}_{\text{bound }}$ Variables in , among ${\mathbf{u}}_{\text{bound }}$ Positive number , The allowable range of scene parameters is defined . Put the... Of each azimuth and elevation ${\mathbf{u}}_{\text{bound }}$ Set as $180^{\circ }$ and $90^{\circ }$.

Differentiable Renderer

Renderers $\mathbf{R}$ With 3D shape $\mathbf{S}$(mesh or point cloud) And scene parameters $\mathbf{u}$ As input , The output is corresponding to $M$ Images ${\left\{{\mathbf{x}}_i\right\}}_{i=1}^M$. because $\mathbf{R}$ Derivable , gradient $\frac{\partial {\mathbf{x}}_i}{\partial \mathbf{u}}$ It can be back propagated from each image to the whole scene parameters , Therefore, we can construct an end-to-end learning framework .

When $\mathbf{S}$ Expressed as 3D mesh when ,$\mathbf{R}$ There are two components ：rasterizer and shader. First , At a given camera angle of view and will face After assigning to pixels ,rasterizer take mesh Transform from the world coordinate system to the view coordinate system . then shader according to face The assignment of creates multiple values for each pixel , And fuse these values .

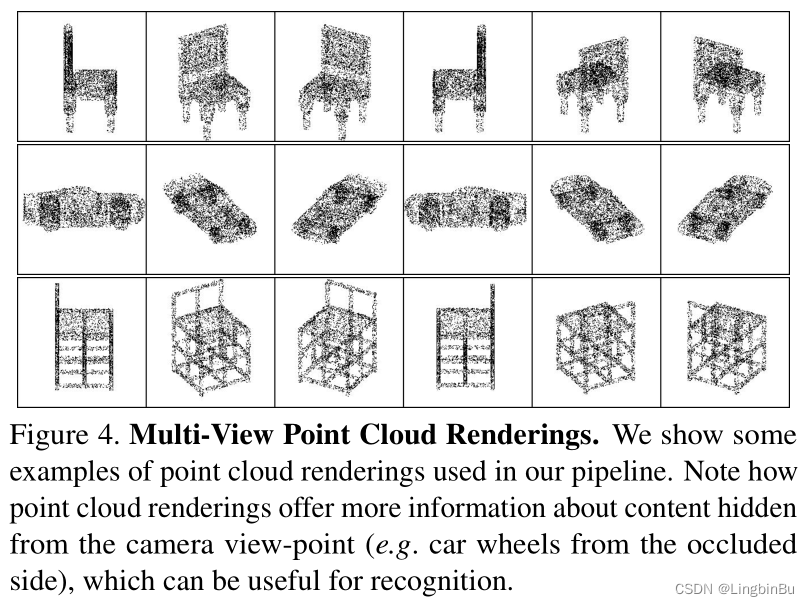
When $\mathbf{S}$ When expressed as point cloud ,$\mathbf{R}$ have access to alpha-blending mechanism.

View-Points Conditioned on 3D Shape

Through the study Multi-View Transformation Network (MVTN)$\mathbf{G}\in {\mathbb{R}}^{P\times 3}\to {\mathbb{R}}^{\tau }$ And parameters ${\mathbf{\theta }}_{\mathbf{G}}$, take $\mathbf{u}$ Designed to 3D A function of shape , among $P$ From the shape $\mathbf{S}$ Number of sampling points .MVTN The training of can be expressed as ：
$$\begin{array}{rl}\underset{{\mathbf{\theta }}_{\mathbf{C}},{\mathbf{\theta }}_{\mathrm{G}}}{\mathrm{argmin}}& \sum _n^{N}L\left(\mathbf{C}\left(\mathbf{R}\left({\mathbf{S}}_n,{\mathbf{u}}_n\right)\right),y_n\right)\text{ s. t. }{\mathbf{u}}_n={\mathbf{u}}_{\text{bound }}\cdot \tanh \left(\mathbf{G}\left({\mathbf{S}}_n\right)\right)\end{array}$$
among $\mathbf{G}$ Yes 3D Shape coding , Predict task specific multiview Networks $\mathbf{C}$ Optimal viewpoint of . because $\mathbf{G}$ The goal of is only to predict the viewpoint, so $\mathbf{G}$ Its structure is very simple , And very light . meanwhile , stay $\mathbf{G}$ A simple point encoder is also used in ( such as PointNet Medium shared MLP), Used to process from $\mathbf{S}$ Got $P$ A little bit , And the generated dimension is $b$ Of coarse Shape features . then shallow MLP From this global shape feature, the scene parameters are regressed ${\mathbf{u}}_n$, In order to predict parameters $\mathbf{u}$ The value of is forced into $\pm {\mathbf{u}}_{\text{bound }}$ Within the scope of , Used tanh Function will $\mathbf{u}$ Zoom to $\pm {\mathbf{u}}_{\text{bound }}$ Inside .

MVTN for 3D Shape Classification

In order to MVTN Training , be used for 3D Shape classification , We define a cross entropy loss function , But other loss functions and regular terms can also be used . Multi perspective network ($\mathbf{C}$) and MVTN($\mathbf{G}$) Use the same loss function to train together . The advantage of our network structure is that it can handle 3D Point cloud . When $\mathbf{S}$ When it is a group of point clouds , Simply put $\mathbf{R}$ Defined as a steerable place cloud renderer .

MVTN for 3D Shape Retrieval

We consider the $\mathbf{C}$ The feature representation of the last layer in front of the classifier , Use LFDA reduction Project these features to other spaces , And take the processed features as signature Describe a shape . In the test phase , shape signature It is used to retrieve the most similar shape in the test set .

experiment

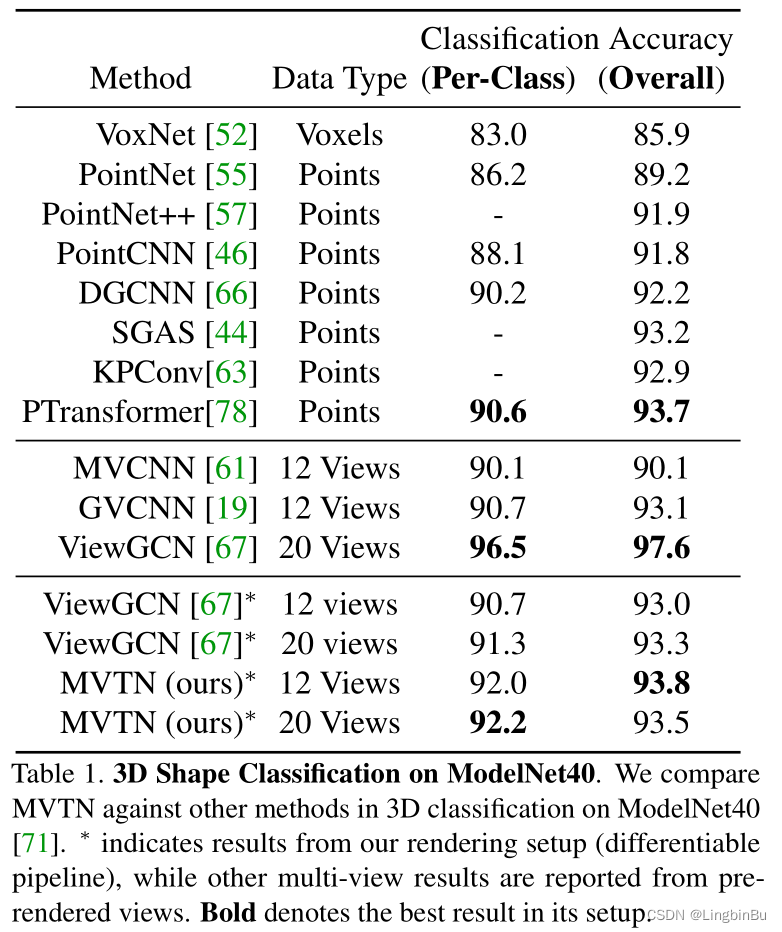
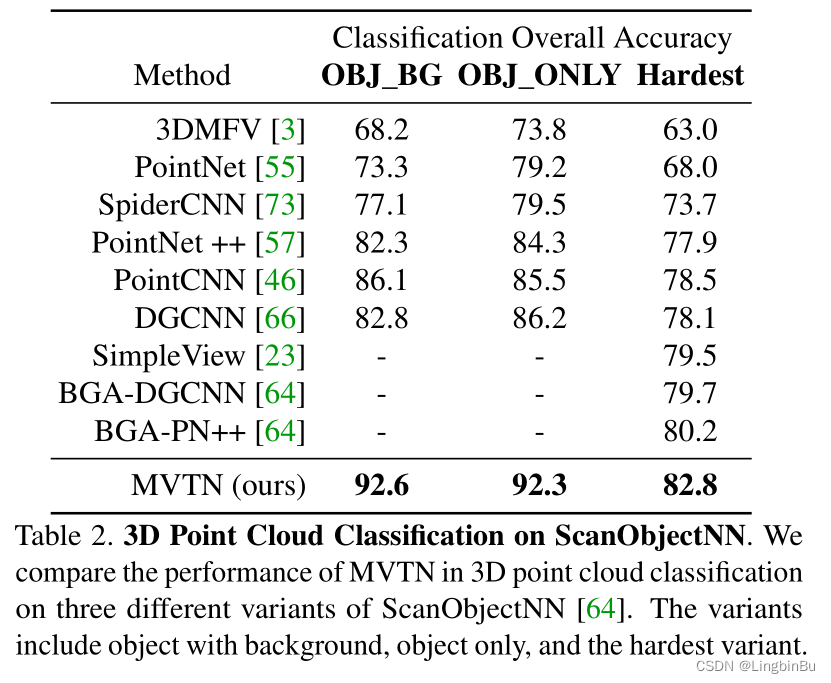
3D Shape Classification

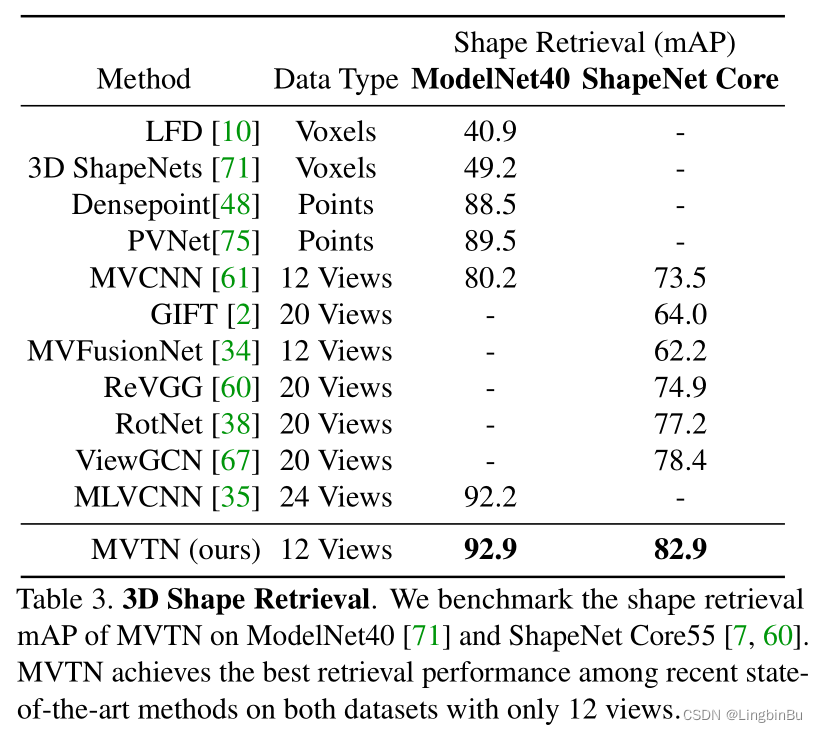
3D Shape Retrieval

Rotation Robustness

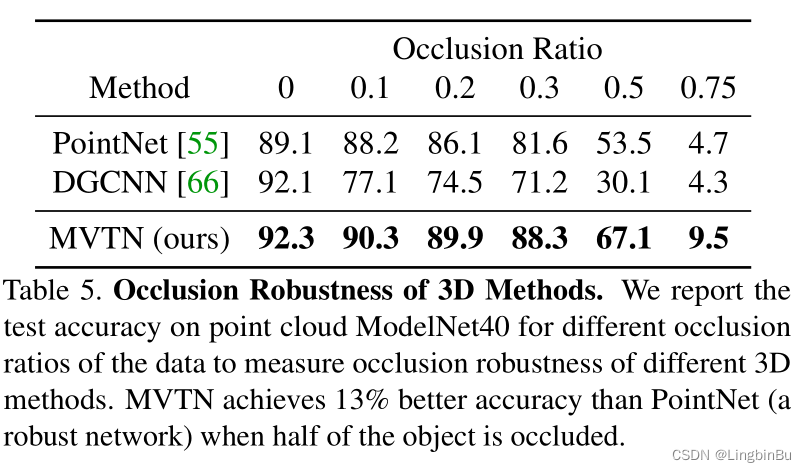
Occlusion Robustness

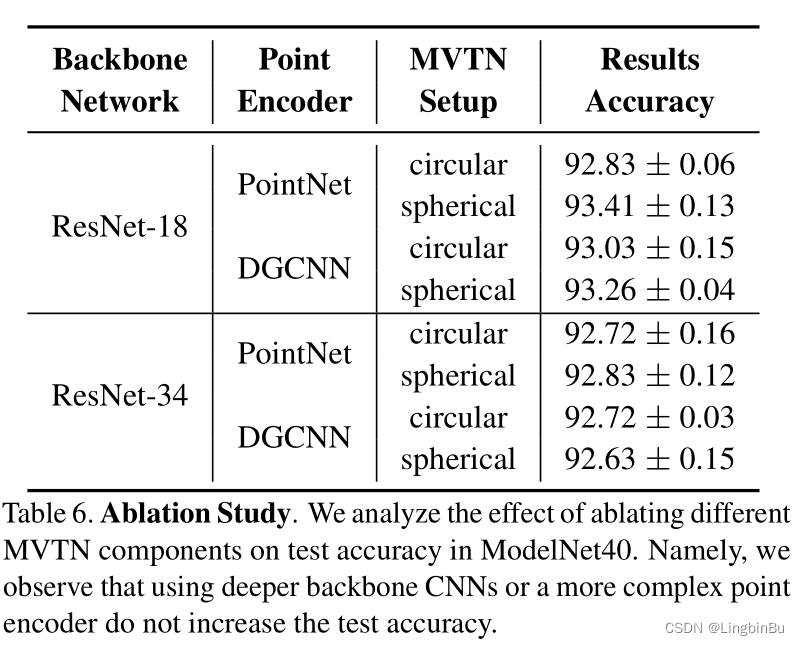
Ablation Study

Number of Views

Choice of Backbone and Point Encoders

Choice of Multi-View Network

Time and Memory Requirements