当前位置:网站首页>【点云处理之论文狂读经典版7】—— Dynamic Edge-Conditioned Filters in Convolutional Neural Networks on Graphs
【点云处理之论文狂读经典版7】—— Dynamic Edge-Conditioned Filters in Convolutional Neural Networks on Graphs
2022-07-03 08:53:00 【LingbinBu】
ECC:图卷积神经神经网络的动态边条件滤波器
摘要
- 背景: 许多问题都可以表示为基于graph结构数据的预测
- 方法: 将卷积操作从网格推广到任意的graphs,同时避免了频域,能够解决不同大小和连通性的graph
- 细节: filters的权值依赖顶点到邻域的边值;开发了用于graph分类的深度神经网络
- 结果: 在点云分类上的效果很好
- 代码:https://github.com/mys007/ecc (PyTorch版本)
1.引言
- 在空间域中构建了一个图卷积神经网络,filters的权值依赖于边上的值,并且对每个特定的输入都动态更新。提出的图卷积网络适用于任意的数据结构
- 将图卷积网络应用到点云分类任务中,并取得到了较好的结果
2.相关工作
频域方法
空间域方法
3.方法
3.1 Edge-Conditioned Convolution
令 l ∈ { 0 , . . , l max } l \in\left\{0, . ., l_{\max }\right\} l∈{ 0,..,lmax}为前馈神经网络层的索引。
令 G = G= G= ( V , E ) (V, E) (V,E)表示无向或有向图,其中 V V V是顶点(Vertex)的有限集合 ∣ V ∣ = n |V|=n ∣V∣=n, E ⊆ V × V E \subseteq V \times V E⊆V×V是边(Edge)的集合 ∣ E ∣ = m |E|=m ∣E∣=m。
假设图是通过顶点和边进行表示的,即 X l : V ↦ R d l X^{l}: V \mapsto \mathbb{R}^{d_{l}} Xl:V↦Rdl表示给每个顶点分配值(feature), L : E ↦ R s L: E \mapsto \mathbb{R}^{s} L:E↦Rs表示给每个边分配值(attribute)。用矩阵的形式可以表示所有的顶点 X l ∈ R n × d l X^{l} \in \mathbb{R}^{n \times d_{l}} Xl∈Rn×dl和所有的边 L ∈ R m × s , X 0 L \in \mathbb{R}^{m \times s}, X^{0} L∈Rm×s,X0表示为输入信号。
顶点 i i i的 neighborhood N ( i ) = { j ; ( j , i ) ∈ E } ∪ { i } N(i)=\{j ;(j, i) \in E\} \cup\{i\} N(i)={ j;(j,i)∈E}∪{ i}包含了所有相邻的顶点和 i i i本身。
顶点 i i i处的filtered信号 X l ( i ) ∈ R d l X^{l}(i) \in \mathbb{R}^{d_{l}} Xl(i)∈Rdl通过其neighborhood点信号 X l − 1 ( j ) ∈ R d l − 1 X^{l-1}(j) \in \mathbb{R}^{d_{l-1}} Xl−1(j)∈Rdl−1, j ∈ N ( i ) j \in N(i) j∈N(i)的加权和计算得到。
尽管这种交换聚合的方式解决了permutation-invariant和neighborhood 大小可变的问题,但是这样也抹除了任意的结构信息。(意思是指聚合的方法太暴力?只用顶点进行更新会损失结构信息,所以引出了边值作为权重)
为了解决这个问题,提出在每个边值上都加入filter权值的条件。定义一个输入为边值 L ( j , i ) L(j, i) L(j,i)的filter-generating network F l : R s ↦ R d l × d l − 1 F^{l}: \mathbb{R}^{s} \mapsto \mathbb{R}^{d_{l} \times d_{l-1}} Fl:Rs↦Rdl×dl−1, 输出为特定边的权值矩阵 Θ j i l ∈ R d l × d l − 1 \Theta_{j i}^{l} \in \mathbb{R}^{d_{l} \times d_{l-1}} Θjil∈Rdl×dl−1,见图1。
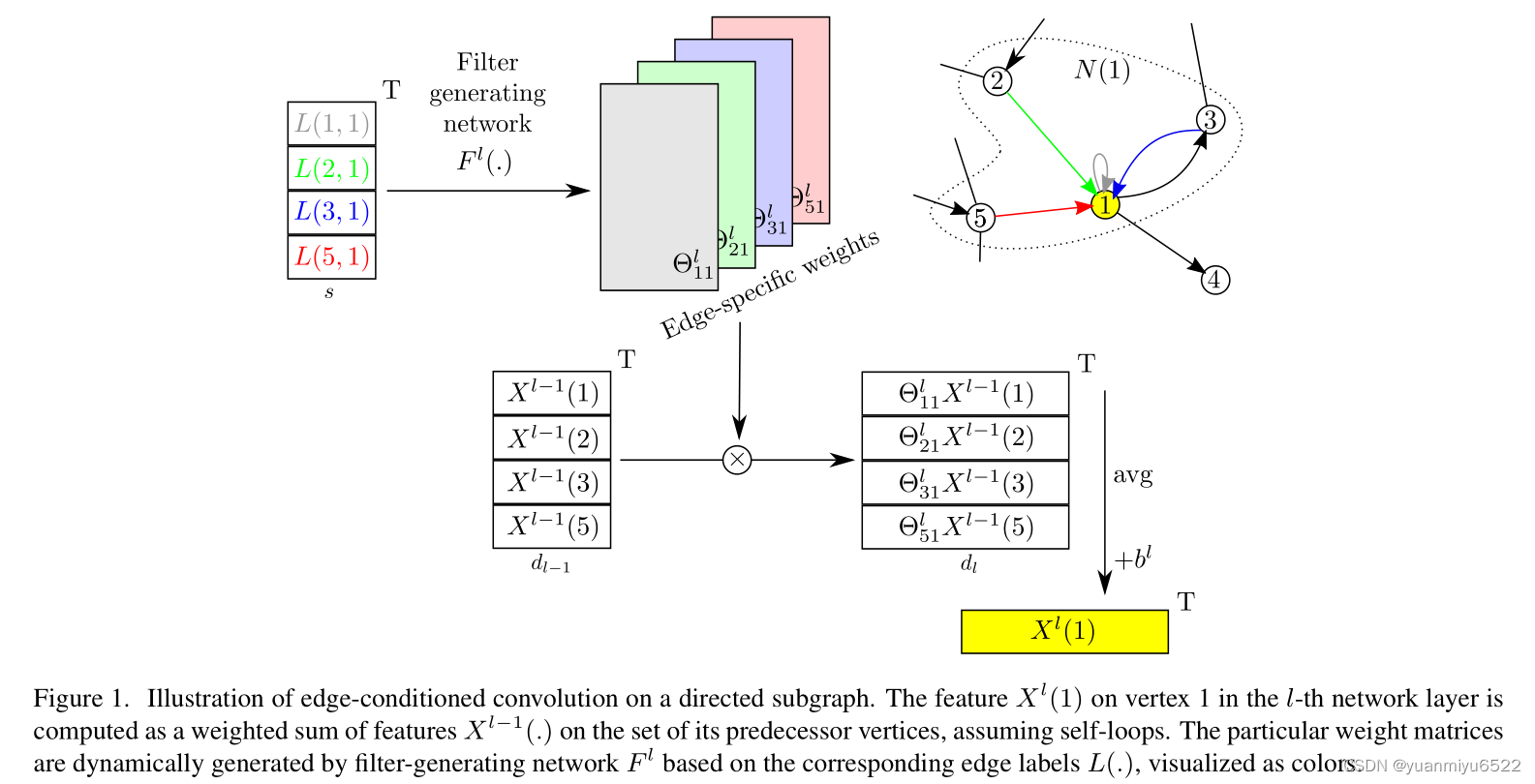
这个被称为 Edge-Conditioned Convolution (ECC) 的卷积操作,用公式可以表示为:
X l ( i ) = 1 ∣ N ( i ) ∣ ∑ j ∈ N ( i ) F l ( L ( j , i ) ; w l ) X l − 1 ( j ) + b l = 1 ∣ N ( i ) ∣ ∑ j ∈ N ( i ) Θ j i l X l − 1 ( j ) + b l \begin{aligned} X^{l}(i) &=\frac{1}{|N(i)|} \sum_{j \in N(i)} F^{l}\left(L(j, i) ; w^{l}\right) X^{l-1}(j)+b^{l} \\ &=\frac{1}{|N(i)|} \sum_{j \in N(i)} \Theta_{j i}^{l} X^{l-1}(j)+b^{l} \end{aligned} Xl(i)=∣N(i)∣1j∈N(i)∑Fl(L(j,i);wl)Xl−1(j)+bl=∣N(i)∣1j∈N(i)∑ΘjilXl−1(j)+bl
其中 b l ∈ R d l b^{l} \in \mathbb{R}^{d_{l}} bl∈Rdl是可学习的偏置, F l F^{l} Fl的可学习参数为网络权值 w l w^{l} wl。 w l w^{l} wl 和 b l b^{l} bl是模型参数,仅在训练时更新, Θ j i l \Theta_{j i}^{l} Θjil是根据输入graph的边值动态生成的参数。filter-generating network F l F^{l} Fl可以是任意可导的模型,本文使用的是多层感知机。
复杂度
对所有顶点计算 X l X^l Xl至多需要 m m m次 F l F^l Fl的评估,以及 m + n m+n m+n(有向图)或 2 m + n 2m+n 2m+n(无向图)次矩阵-向量乘法运算。但是在GPU上进行操作会更有效率一些。
3.2 Relationship to Existing Formulations
在规则的网格上进行卷积可以看作是ECC的一种特殊形式。

3.3. Deep Networks with ECC
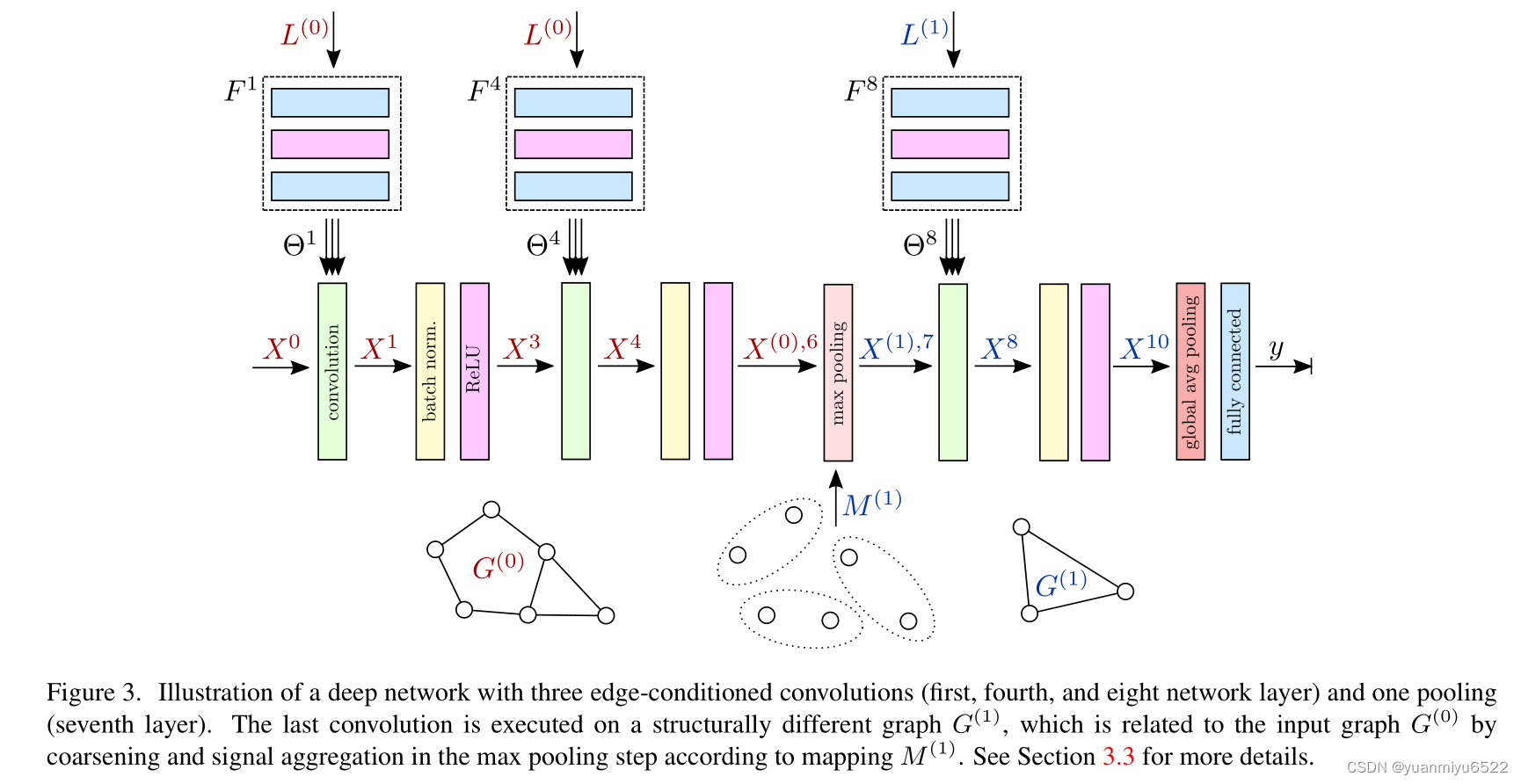
网络结构包括交错卷积、全局池化和全连接层组成,见图3。通过这种方式,从局部邻域中得到的信息会逐层结合得到最终的context(增大接受域)。虽然边值对特定的graph来说是固定的,但通过filter generating networks进行了(学习的)解释,可能会从一层到另外一层时发生改变(在层之间未共享 F l F^l Fl的权重)。 因此,只有1-hop neighborhoods限制的ECC并不会被约束,类似于在标准CNN中使用小的3×3filter来换取更深的网络,这是有益的。
在每次卷积后使用Batch Normalization,用于快速收敛。
Pooling
尽管(non-strided)卷积层和所有point-wise层不会改变基础graph,并且只能在顶点上更新信号,但池化层被定义为在一个新的、coarsened graph的顶点上输出聚合信号。因此,必须为每个输入graph构造一个逐步coarser的graph h m a x h_{max} hmax的pyramid。
令 h ∈ { 0 , … , h max } h \in\left\{0, \ldots, h_{\max }\right\} h∈{ 0,…,hmax}表示pyramid中不同的 graph G ( h ) = ( V ( h ) , E ( h ) ) G^{(h)}=\left(V^{(h)}, E^{(h)}\right) G(h)=(V(h),E(h)),每一个 G ( h ) G^{(h)} G(h)都与 L ( h ) L^{(h)} L(h)和 X ( h ) , l X^{(h), l} X(h),l相关联。coarsening的过程包含3步:
- subsampling or merging vertices
- creating the new edge structure E ( h ) E^{(h)} E(h) and labeling L ( h ) L^{(h)} L(h) (so-called reduction)
- mapping the vertices in the original graph to those in the coarsened one with M ( h ) : V ( h − 1 ) ↦ V ( h ) M^{(h)}: V^{(h-1)} \mapsto V^{(h)} M(h):V(h−1)↦V(h)
最终,索引为 l h l_{h} lh的池化层将 X ( h − 1 ) , l h − 1 X^{(h-1), l_{h-1}} X(h−1),lh−1聚合到基于 M ( h ) M^{(h)} M(h)的更低维度 X ( h ) , l h X^{(h), l_{h}} X(h),lh。
在coarsening的过程中,由于self-edge经常出现,因此会出现较小的graph减少为若干断开连接的顶点,这样也不会出现问题。因为该结构被用来处理带有变量 n , m n,m n,m的graph,我们通过全局 average/max池化操作解决最低分辨率下graph的变化的顶点数量 n h m a x n^{h_{max}} nhmax。
3.4. Application in Point Clouds
Graph Construction
给定一组点云 P P P 和对应的点特征 X P X_{P} XP,我们构造一个有向图 G = ( V , E ) G=(V, E) G=(V,E),并分配 X 0 X^{0} X0 和 L L L。
- 对于每个点 p ∈ P p \in P p∈P都构造顶点 i ∈ V i \in V i∈V,通过 X 0 ( i ) = X P ( p ) X^{0}(i)=X_{P}(p) X0(i)=XP(p)分配对应的信号(如果没有特征,那么赋值为0)
- 通过有向边 ( j , i ) (j, i) (j,i)连接每个顶点 i i i 和其在空间neighborhood中的顶点 j j j ,实验表明,Ball query的表现更好
- 在笛卡尔坐标系和球面坐标系下,6D向量 L ( j , i ) = ( δ x , δ y , δ z , ∥ δ ∥ , arccos δ z / ∥ δ ∥ , arctan δ y / δ x ) L(j, i)=\left(\delta_{x}, \delta_{y}, \delta_{z},\|\delta\|, \arccos \delta_{z} /\|\delta\|, \arctan \delta_{y} / \delta_{x}\right) L(j,i)=(δx,δy,δz,∥δ∥,arccosδz/∥δ∥,arctanδy/δx)被作为边上的值,其中 δ = p j − p i \delta=p_{j}-p_{i} δ=pj−pi表示顶点 j , i j,i j,i间的偏移。
Graph Coarsening
对于一组输入点云 P P P,通过VoxelGrid algorithm获得下采样点云的pyramid P ( h ) P^{(h)} P(h),具体流程包括在点云上覆盖上分辨率为 r ( h ) r^{(h)} r(h)的网格,对每个voxel中的点取质心。每个下采样后的点云 P ( h ) P^{(h)} P(h)都被独立转化成neighborhood 半径为 ρ ( h ) \rho^{(h)} ρ(h)的graph G ( h ) G^{(h)} G(h)和 labeling L ( h ) L^{(h)} L(h)。定义pooling map M ( h ) M^{(h)} M(h),保证 P ( h − 1 ) P^{(h-1)} P(h−1)中的每个点都被分配给下采样点云 P ( h ) P^{(h)} P(h)中距离其( P ( h − 1 ) P^{(h-1)} P(h−1)中的每个点)最近的点。
Data Augmentation
We randomly rotate point clouds about their upaxis, jitter their scale, perform mirroring, or delete random points.
4.实验
C ( c ) \mathrm{C}(c) C(c)表示ECC的输出通道数为 c c c,后面跟着batch normalization和ReLU激活函数。 M P ( r , ρ ) \mathrm{MP}(r, \rho) MP(r,ρ)表示最大池化层,grid分辨率为 r r r,neighborhood半径为 ρ \rho ρ。 G A P \mathrm{GAP} GAP为平均池化层。 F C ( c ) \mathrm{FC}(c) FC(c)是通道数为 c c c的全连接层。 D ( p ) \mathrm{D}(p) D(p)表示概率为 p p p的dropouot。
4.1 Sydney Urban Objects

C ( 16 ) − C ( 32 ) − M P ( 0.25 , 0.5 ) − C ( 32 ) − C ( 32 ) − M P ( 0.75 , 1.5 ) − C ( 64 ) − M P ( 1.5 , 1.5 ) − G A P − F C ( 64 ) − D ( 0.2 ) − F C ( 14 ) C(16)-C(32)-MP(0.25,0.5)-C(32)-C(32)-MP(0.75,1.5)-C(64)-MP(1.5,1.5)-GAP-FC(64)-D(0.2)-FC(14) C(16)−C(32)−MP(0.25,0.5)−C(32)−C(32)−MP(0.75,1.5)−C(64)−MP(1.5,1.5)−GAP−FC(64)−D(0.2)−FC(14)
C C C里面的 F l F^l Fl包含 F C ( 16 ) − F C ( 32 ) − F C ( d l d l − 1 ) FC(16)-FC(32)-FC(d_ld_{l−1}) FC(16)−FC(32)−FC(dldl−1)

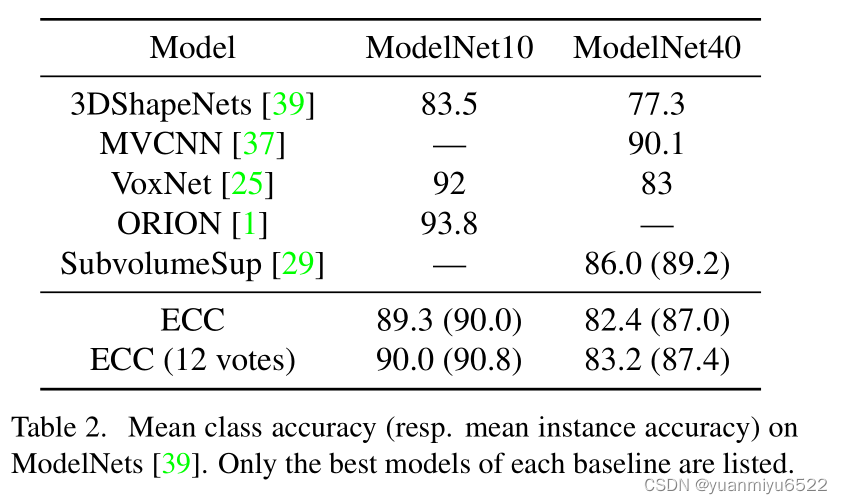
4.2 ModelNet
C ( 16 ) − C ( 32 ) − M P ( 2.5 / 32 , 7.5 / 32 ) − C ( 32 ) − C ( 32 ) − M P ( 7.5 / 32 , 22.5 / 32 ) − C ( 64 ) − G A P − F C ( 64 ) − D ( 0.2 ) − F C ( 10 ) C(16)-C(32)-MP(2.5/32,7.5/32)-C(32)-C(32)-MP(7.5/32,22.5/32)-C(64)-GAP-FC(64)-D(0.2)-FC(10) C(16)−C(32)−MP(2.5/32,7.5/32)−C(32)−C(32)−MP(7.5/32,22.5/32)−C(64)−GAP−FC(64)−D(0.2)−FC(10)
C C C里面的 F l F^l Fl包含 F C ( 16 ) − F C ( 32 ) − F C ( d l d l − 1 ) FC(16)-FC(32)-FC(d_ld_{l−1}) FC(16)−FC(32)−FC(dldl−1)
生词
- commutative adj. 可交换的
- interlace v. 隔行,交错
边栏推荐
- Instant messaging IM is the countercurrent of the progress of the times? See what jnpf says
- TP5 multi condition sorting
- MySQL index types B-tree and hash
- AcWing 787. 归并排序(模板)
- LeetCode 438. Find all letter ectopic words in the string
- Escape from heaven and forget what he suffered. In ancient times, it was called the punishment of escape from heaven. Article collection
- LeetCode 30. Concatenate substrings of all words
- Memory search acwing 901 skiing
- Using variables in sed command
- AcWing 787. Merge sort (template)
猜你喜欢
浅谈企业信息化建设
Recommend a low code open source project of yyds

AcWing 785. 快速排序(模板)
Binary tree traversal (first order traversal. Output results according to first order, middle order, and last order)

树形DP AcWing 285. 没有上司的舞会
Vscode connect to remote server
AcWing 787. 归并排序(模板)

干货!零售业智能化管理会遇到哪些问题?看懂这篇文章就够了

拯救剧荒,程序员最爱看的高分美剧TOP10
【点云处理之论文狂读经典版11】—— Mining Point Cloud Local Structures by Kernel Correlation and Graph Pooling
随机推荐
LeetCode 515. Find the maximum value in each tree row
LeetCode 508. The most frequent subtree elements and
LeetCode 715. Range module
What is the difference between sudo apt install and sudo apt -get install?
拯救剧荒,程序员最爱看的高分美剧TOP10
Sword finger offer II 091 Paint the house
Deep parsing (picture and text) JVM garbage collector (II)
推荐一个 yyds 的低代码开源项目
Methods of checking ports according to processes and checking processes according to ports
Format - C language project sub file
求组合数 AcWing 886. 求组合数 II
AcWing 786. Number k
Find the combination number acwing 885 Find the combination number I
数字化管理中台+低代码,JNPF开启企业数字化转型的新引擎
LeetCode 75. 颜色分类
Alibaba canal actual combat
Noip 2002 popularity group selection number
浅谈企业信息化建设
SQL statement error of common bug caused by Excel cell content that is not paid attention to for a long time
Find the combination number acwing 886 Find the combination number II