当前位置:网站首页>5阶多项式轨迹
5阶多项式轨迹
2022-07-06 23:39:00 【不懂音乐的欣赏者】
前提条件
- 为了获得一条速度连续的轨迹,则该轨迹中每段轨迹需要满足位置和速度约束(4个边界条件),即前一段轨迹 J i − 1 J_{i-1} Ji−1的终点位置和速度要和后一段轨迹 J i J_{i} Ji的位置速度相同,因此使用三阶多项式来表示每段轨迹。
- 为了获得一条加速度连续的轨迹,则该轨迹中每段轨迹需要满足位置、速度和加速度约束(6个边界条件),即前一段轨迹 J i − 1 J_{i-1} Ji−1的终点位置、速度和加速度要和后一段轨迹 J i J_{i} Ji的位置、速度和加速度相同,因此使用五阶多项式来表示每段轨迹。
正文
对于一条轨迹而言,通常可以将一条连续轨迹分段成多段多项式轨迹,这里考虑每段轨迹使用5阶多项式来表示。其中每段轨迹对应的时间均从 0 0 0开始到 T i T_i Ti结束,即对于第 i i i段轨迹 J i J_i Ji而言,其开始时间为 0 0 0,结束时间为 T i T_i Ti,起始位置、速度、加速度分别为 p i p_i pi、 v i v_i vi和 a i a_i ai。根据多项式轨迹的定义
p = c 0 + c 1 t + c 2 t 2 + c 3 t 3 + c 4 t 4 + c 5 t 5 v = c 1 + 2 c 2 t + 3 c 3 t 2 + 4 c 4 t 3 + 5 c 5 t 4 a = 2 c 2 + 6 c 3 t + 12 c 4 t 2 + 20 c 5 t 3 j e r k = 6 c 3 + 24 c 4 t + 60 c 5 t 2 s n a p = 24 c 4 + 120 c 5 t . ( 公 式 1 ) \begin{aligned} p&=c_{0}+c_{1}t+c_{2}t^2+c_{3}t^3+c_{4}t^4+c_{5}t^5 \\ v&=\quad\quad c_{1}+2c_{2}t+3c_{3}t^2+4c_{4}t^3+5c_{5}t^4 \\ a&=\quad\quad\quad\quad2c_{2}+6c_{3}t+12c_{4}t^2+20c_{5}t^3 \\ jerk&=\quad\quad\quad\quad\quad\quad \quad6c_{3}+24c_{4}t+60c_{5}t^2 \\ snap&=\quad\quad\quad\quad\quad\quad \quad\quad \quad\quad 24c_{4}+120c_{5}t. \quad\quad(公式1)\\ \end{aligned} pvajerksnap=c0+c1t+c2t2+c3t3+c4t4+c5t5=c1+2c2t+3c3t2+4c4t3+5c5t4=2c2+6c3t+12c4t2+20c5t3=6c3+24c4t+60c5t2=24c4+120c5t.(公式1)
以第 1 1 1段轨迹为例,将 t = 0 t=0 t=0带入(公式1)可以得第一段轨迹开始时:
p 1 ( 0 ) = c 10 , v 1 ( 0 ) = c 11 , a 1 ( 0 ) = 2 c 12 . \begin{aligned} p_1(0)&=c_{10}, \\ v_1(0)&=c_{11},\\ a_1(0)&=2c_{12}. \end{aligned} p1(0)v1(0)a1(0)=c10,=c11,=2c12.
将 t = T 1 t=T_1 t=T1带入(公式1)可以得到初始时第一段轨迹结束时:
p 1 ( T 1 ) = c 10 + c 11 ( T 1 − 0 ) + c 12 ( T 1 − 0 ) 2 + c 13 ( T 1 − 0 ) 3 + c 14 ( T 1 − 0 ) 4 + c 15 ( T 1 − 0 ) 5 = c 10 + c 11 T 1 + c 12 T 1 2 + c 13 T 1 3 + c 14 T 1 4 + c 15 T 1 5 , v 1 ( T 1 ) = c 11 + 2 c 12 ( T 1 − 0 ) + 3 c 13 ( T 1 − 0 ) 2 + 4 c 14 ( T 1 − 0 ) 3 + 5 c 15 ( T 1 − 0 ) 4 = c 11 + 2 c 12 ( T 1 ) + 3 c 13 ( T 1 ) 2 + 4 c 14 ( T 1 ) 3 + 5 c 15 ( T 1 ) 4 , a 1 ( T 1 ) = 2 c 12 + 6 c 13 ( T 1 − 0 ) + 12 c 14 ( T 1 − 0 ) 2 + 20 c 15 ( T 1 − 0 ) 3 = 2 c 12 + 6 c 13 ( T 1 ) + 12 c 14 ( T 1 ) 2 + 20 c 15 ( T 1 ) 3 . \begin{aligned} p_1(T_1)&=c_{10}+c_{11}(T_1-0)+c_{12}(T_1-0)^2+c_{13}(T_1-0)^3+c_{14}(T_1-0)^4+c_{15}(T_1-0)^5 \\ & = c_{10}+c_{11}T_1+c_{12}T_1^2+c_{13}T_1^3+c_{14}T_1^4+c_{15}T_1^5, \\ v_1(T_1)&=c_{11}+2c_{12}(T_1-0)+3c_{13}(T_1-0)^2+4c_{14}(T_1-0)^3+5c_{15}(T_1-0)^4 \\ & = c_{11}+2c_{12}(T_1)+3c_{13}(T_1)^2+4c_{14}(T_1)^3+5c_{15}(T_1)^4, \\ a_1(T_1)&=2c_{12}+6c_{13}(T_1-0)+12c_{14}(T_1-0)^2+20c_{15}(T_1-0)^3\\ & = 2c_{12}+6c_{13}(T_1)+12c_{14}(T_1)^2+20c_{15}(T_1)^3. \end{aligned} p1(T1)v1(T1)a1(T1)=c10+c11(T1−0)+c12(T1−0)2+c13(T1−0)3+c14(T1−0)4+c15(T1−0)5=c10+c11T1+c12T12+c13T13+c14T14+c15T15,=c11+2c12(T1−0)+3c13(T1−0)2+4c14(T1−0)3+5c15(T1−0)4=c11+2c12(T1)+3c13(T1)2+4c14(T1)3+5c15(T1)4,=2c12+6c13(T1−0)+12c14(T1−0)2+20c15(T1−0)3=2c12+6c13(T1)+12c14(T1)2+20c15(T1)3.
同理可得第二段轨迹开始时:
p 2 ( 0 ) = c 20 , v 2 ( 0 ) = c 21 , a 2 ( 0 ) = 2 c 22 . \begin{aligned} p_2(0)&=c_{20}, \\ v_2(0)&=c_{21},\\ a_2(0)&=2c_{22}. \end{aligned} p2(0)v2(0)a2(0)=c20,=c21,=2c22.
由于一条轨迹是由多段多项式轨迹组成,因此需要满足:
{ c 10 = p 1 ( 0 ) : 起 始 位 置 边 界 条 件 c 11 = v 1 ( 0 ) : 起 始 速 度 边 界 条 件 2 c 12 = a 1 ( 0 ) : 起 始 加 速 度 边 界 条 件 前 一 段 轨 迹 终 止 j e r k 与 后 一 段 轨 迹 起 始 s n a p 相 同 , 无 j e r k 大 小 约 束 , 即 j e r k 1 ( T 1 ) − j e r k 2 ( 0 ) = 0 6 c 13 + 24 c 14 T 1 + 60 c 15 T 1 2 − 6 c 23 = 0 前 一 段 轨 迹 终 止 s n a p 与 后 一 段 轨 迹 起 始 s n a p 相 同 , 无 s n a p 大 小 约 束 , 即 s n a p 1 ( T 1 ) − s n a p 2 ( 0 ) = 0 24 c 14 + 120 T 1 − 24 c 24 = 0 前 一 段 轨 迹 终 止 位 置 与 后 一 段 轨 迹 起 始 位 置 相 同 , 即 p 1 ( T 1 ) = p 2 ( 0 ) : c 10 + c 11 T 1 + c 12 T 1 2 + c 13 T 1 3 + c 14 T 1 4 + c 15 T 1 5 = p 2 ( 0 ) c 10 + c 11 T 1 + c 12 T 1 2 + c 13 T 1 3 + c 14 T 1 4 + c 15 T 1 5 − c 20 = 0 前 一 段 轨 迹 终 止 位 置 与 后 一 段 轨 迹 起 始 速 度 相 同 , 即 v 1 ( T 1 ) − v 2 ( 0 ) = 0 c 11 + 2 c 12 T 1 + 3 c 13 T 1 2 + 4 c 14 T 1 3 + 5 c 15 T 1 4 − c 21 = 0 前 一 段 轨 迹 终 止 位 置 与 后 一 段 轨 迹 起 始 加 速 度 相 同 , 即 a 1 ( T 1 ) − a 2 ( 0 ) = 0 2 c 12 + 6 c 13 T 1 + 12 c 14 T 1 2 + 20 c 15 T 1 3 − 2 c 22 = 0 \left\{\begin{aligned} &c_{10}=p_1(0):起始位置边界条件 \\ &c_{11}=v_1(0):起始速度边界条件 \\ &2c_{12}=a_1(0):起始加速度边界条件 \\ &前一段轨迹终止jerk与后一段轨迹起始snap相同,无jerk大小约束,即jerk_1(T_1)-jerk_2(0)=0\\ &6c_{13}+24c_{14}T_1+60c_{15}T_1^2-6c_{23}=0\\ &前一段轨迹终止snap与后一段轨迹起始snap相同,无snap大小约束,即snap_1(T_1)-snap_2(0)=0\\ &24c_{14}+120T_1-24c_{24}=0\\ &前一段轨迹终止位置与后一段轨迹起始位置相同,即p_1(T_1)=p_2(0):\\ &c_{10}+c_{11}T_1+c_{12}T_1^2+c_{13}T_1^3+c_{14}T_1^4+c_{15}T_1^5=p_2(0)\\ &c_{10}+c_{11}T_1+c_{12}T_1^2+c_{13}T_1^3+c_{14}T_1^4+c_{15}T_1^5-c_{20}=0\\ &前一段轨迹终止位置与后一段轨迹起始速度相同,即v_1(T_1)-v_2(0)=0\\ &c_{11}+2c_{12}T_1+3c_{13}T_1^2+4c_{14}T_1^3+5c_{15}T_1^4-c_{21}=0\\ &前一段轨迹终止位置与后一段轨迹起始加速度相同,即a_1(T_1)-a_2(0)=0\\ &2c_{12}+6c_{13}T_1+12c_{14}T_1^2+20c_{15}T_1^3-2c_{22}=0\\ \end{aligned}\right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧c10=p1(0):起始位置边界条件c11=v1(0):起始速度边界条件2c12=a1(0):起始加速度边界条件前一段轨迹终止jerk与后一段轨迹起始snap相同,无jerk大小约束,即jerk1(T1)−jerk2(0)=06c13+24c14T1+60c15T12−6c23=0前一段轨迹终止snap与后一段轨迹起始snap相同,无snap大小约束,即snap1(T1)−snap2(0)=024c14+120T1−24c24=0前一段轨迹终止位置与后一段轨迹起始位置相同,即p1(T1)=p2(0):c10+c11T1+c12T12+c13T13+c14T14+c15T15=p2(0)c10+c11T1+c12T12+c13T13+c14T14+c15T15−c20=0前一段轨迹终止位置与后一段轨迹起始速度相同,即v1(T1)−v2(0)=0c11+2c12T1+3c13T12+4c14T13+5c15T14−c21=0前一段轨迹终止位置与后一段轨迹起始加速度相同,即a1(T1)−a2(0)=02c12+6c13T1+12c14T12+20c15T13−2c22=0
将上述约束转换成矩阵Ax=b形式,可得:
x = [ c 10 c 11 c 12 c 13 c 14 c 15 c 20 c 21 c 22 c 23 c 24 c 25 ] x=\begin{bmatrix} c_{10}\\ c_{11}\\ c_{12} \\ c_{13} \\ c_{14} \\ c_{15} \\ c_{20} \\ c_{21} \\ c_{22} \\ c_{23} \\ c_{24} \\ c_{25} \\ \end{bmatrix} x=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡c10c11c12c13c14c15c20c21c22c23c24c25⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
b = [ p 1 ( 0 ) v 1 ( 0 ) a 1 ( 0 ) 0 0 p 2 ( 0 ) 0 0 0 ] b=\begin{bmatrix} {p_1(0)}\\ {v_1(0)}\\ {a_1(0)}\\ 0\\ 0\\ p_2(0)\\ 0\\ 0\\ 0\\ \\ \end{bmatrix} b=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡p1(0)v1(0)a1(0)00p2(0)000⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
构建A矩阵如下:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 1 1 | |||||||||||
| 1 | 1 1 1 | |||||||||||
| 2 | 2 2 2 | |||||||||||
| 3 | 6 6 6 | 24 T 1 24T_1 24T1 | 60 T 1 2 60T_1^2 60T12 | − 6 -6 −6 | ||||||||
| 4 | 24 24 24 | 120 T 1 120T_1 120T1 | − 24 -24 −24 | |||||||||
| 5 | 1 1 1 | T 1 T_1 T1 | T 1 2 T_1^2 T12 | T 1 3 T_1^3 T13 | T 1 4 T_1^4 T14 | T 1 5 T_1^5 T15 | ||||||
| 6 | 1 1 1 | T 1 T_1 T1 | T 1 2 T_1^2 T12 | T 1 3 T_1^3 T13 | T 1 4 T_1^4 T14 | T 1 5 T_1^5 T15 | − 1 -1 −1 | |||||
| 7 | 1 1 1 | 2 T 1 2T_1 2T1 | 3 T 1 2 3T_1^2 3T12 | 4 T 1 3 4T_1^3 4T13 | 5 T 1 4 5T_1^4 5T14 | − 1 -1 −1 | ||||||
| 8 | 2 2 2 | 6 T 6T 6T | 12 T 1 2 12T_1^2 12T12 | 20 T 1 3 20T_1^3 20T13 | − 2 -2 −2 | |||||||
| 9 | … | |||||||||||
| 10 | 1 1 1 | T 2 T_2 T2 | T 2 2 T_2^2 T22 | T 2 3 T_2^3 T23 | T 2 4 T_2^4 T24 | T 2 5 T_2^5 T25 | ||||||
| 11 | 1 1 1 | 2 T 2 2T_2 2T2 | 3 T 2 2 3T_2^2 3T22 | 4 T 2 3 4T_2^3 4T23 | 5 T 2 4 5T_2^4 5T24 | |||||||
| 12 | 2 2 2 | 6 T 2 6T_2 6T2 | 12 T 2 2 12T_2^2 12T22 | 20 T 2 3 20T_2^3 20T23 |
注:红色是行/列标号。
inline void generate(const Eigen::MatrixXd &inPs,
const Eigen::VectorXd &ts)
{
T1 = ts;
T2 = T1.cwiseProduct(T1);
T3 = T2.cwiseProduct(T1);
T4 = T2.cwiseProduct(T2);
T5 = T4.cwiseProduct(T1);
A.reset();
b.setZero();
A(0, 0) = 1.0;
A(1, 1) = 1.0;
A(2, 2) = 2.0;
b.row(0) = headPVA.col(0).transpose();
b.row(1) = headPVA.col(1).transpose();
b.row(2) = headPVA.col(2).transpose();
for (int i = 0; i < N - 1; i++)
{
A(6 * i + 3, 6 * i + 3) = 6.0;
A(6 * i + 3, 6 * i + 4) = 24.0 * T1(i);
A(6 * i + 3, 6 * i + 5) = 60.0 * T2(i);
A(6 * i + 3, 6 * i + 9) = -6.0;
A(6 * i + 4, 6 * i + 4) = 24.0;
A(6 * i + 4, 6 * i + 5) = 120.0 * T1(i);
A(6 * i + 4, 6 * i + 10) = -24.0;
A(6 * i + 5, 6 * i) = 1.0;
A(6 * i + 5, 6 * i + 1) = T1(i);
A(6 * i + 5, 6 * i + 2) = T2(i);
A(6 * i + 5, 6 * i + 3) = T3(i);
A(6 * i + 5, 6 * i + 4) = T4(i);
A(6 * i + 5, 6 * i + 5) = T5(i);
A(6 * i + 6, 6 * i) = 1.0;
A(6 * i + 6, 6 * i + 1) = T1(i);
A(6 * i + 6, 6 * i + 2) = T2(i);
A(6 * i + 6, 6 * i + 3) = T3(i);
A(6 * i + 6, 6 * i + 4) = T4(i);
A(6 * i + 6, 6 * i + 5) = T5(i);
A(6 * i + 6, 6 * i + 6) = -1.0;
A(6 * i + 7, 6 * i + 1) = 1.0;
A(6 * i + 7, 6 * i + 2) = 2 * T1(i);
A(6 * i + 7, 6 * i + 3) = 3 * T2(i);
A(6 * i + 7, 6 * i + 4) = 4 * T3(i);
A(6 * i + 7, 6 * i + 5) = 5 * T4(i);
A(6 * i + 7, 6 * i + 7) = -1.0;
A(6 * i + 8, 6 * i + 2) = 2.0;
A(6 * i + 8, 6 * i + 3) = 6 * T1(i);
A(6 * i + 8, 6 * i + 4) = 12 * T2(i);
A(6 * i + 8, 6 * i + 5) = 20 * T3(i);
A(6 * i + 8, 6 * i + 8) = -2.0;
b.row(6 * i + 5) = inPs.col(i).transpose();
}
A(6 * N - 3, 6 * N - 6) = 1.0;
A(6 * N - 3, 6 * N - 5) = T1(N - 1);
A(6 * N - 3, 6 * N - 4) = T2(N - 1);
A(6 * N - 3, 6 * N - 3) = T3(N - 1);
A(6 * N - 3, 6 * N - 2) = T4(N - 1);
A(6 * N - 3, 6 * N - 1) = T5(N - 1);
A(6 * N - 2, 6 * N - 5) = 1.0;
A(6 * N - 2, 6 * N - 4) = 2 * T1(N - 1);
A(6 * N - 2, 6 * N - 3) = 3 * T2(N - 1);
A(6 * N - 2, 6 * N - 2) = 4 * T3(N - 1);
A(6 * N - 2, 6 * N - 1) = 5 * T4(N - 1);
A(6 * N - 1, 6 * N - 4) = 2;
A(6 * N - 1, 6 * N - 3) = 6 * T1(N - 1);
A(6 * N - 1, 6 * N - 2) = 12 * T2(N - 1);
A(6 * N - 1, 6 * N - 1) = 20 * T3(N - 1);
b.row(6 * N - 3) = tailPVA.col(0).transpose();
b.row(6 * N - 2) = tailPVA.col(1).transpose();
b.row(6 * N - 1) = tailPVA.col(2).transpose();
A.factorizeLU();
A.solve(b);
return;
边栏推荐
- How does redis implement multiple zones?
- Initial experience of annotation
- 利用OPNET进行网络任意源组播(ASM)仿真的设计、配置及注意点
- 照片选择器CollectionView
- MySQL数据库学习(8) -- mysql 内容补充
- Y58. Chapter III kubernetes from entry to proficiency - continuous integration and deployment (Sany)
- Harmonyos fourth training
- 《2》 Label
- Longest non descent subsequence (LIS) (dynamic programming)
- 数字化创新驱动指南
猜你喜欢

【js组件】date日期显示。

DOM-节点对象+时间节点 综合案例

在米家、欧瑞博、苹果HomeKit趋势下,智汀如何从中脱颖而出?
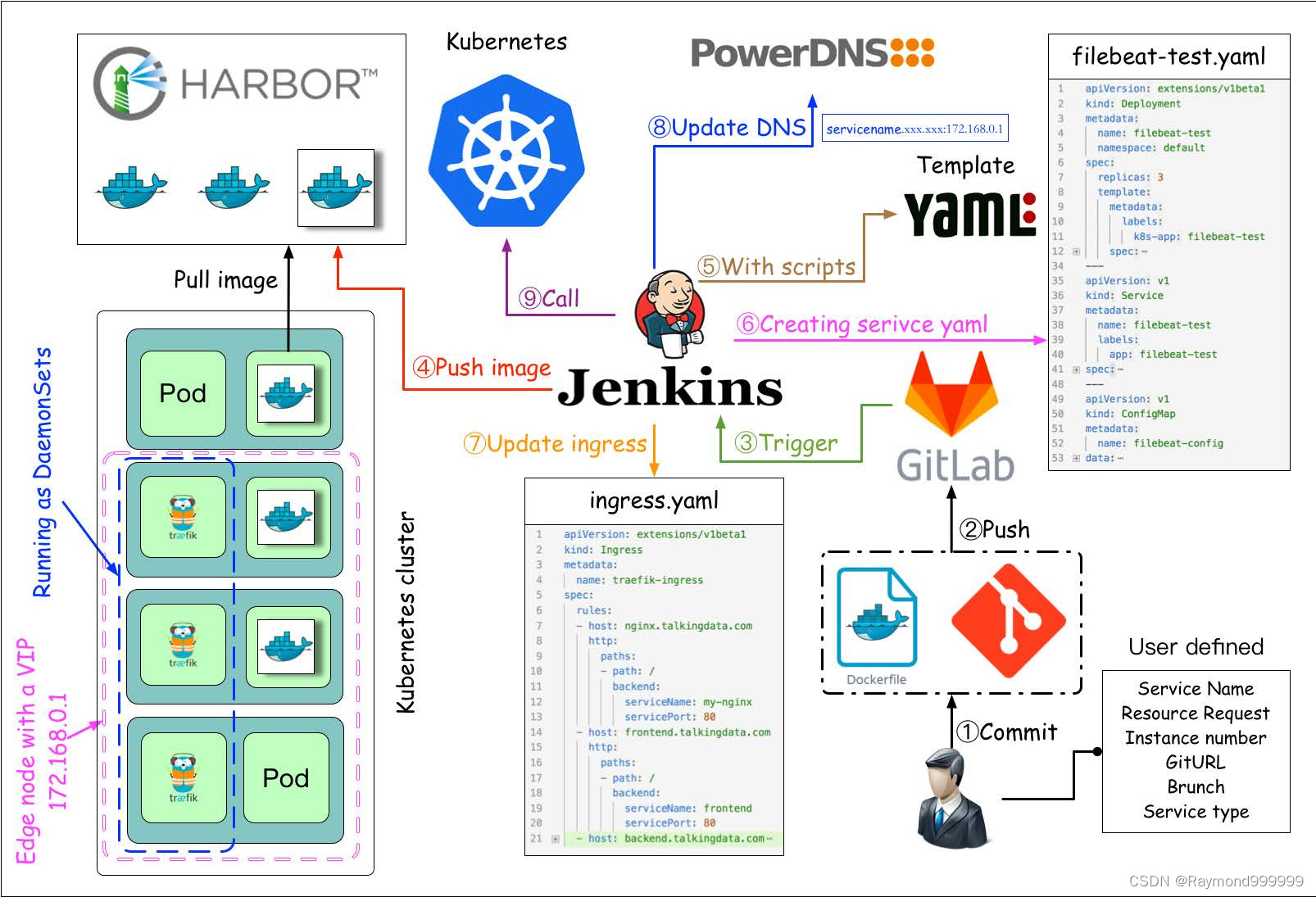
Y58. Chapter III kubernetes from entry to proficiency - continuous integration and deployment (Sany)

JVM (XX) -- performance monitoring and tuning (I) -- Overview
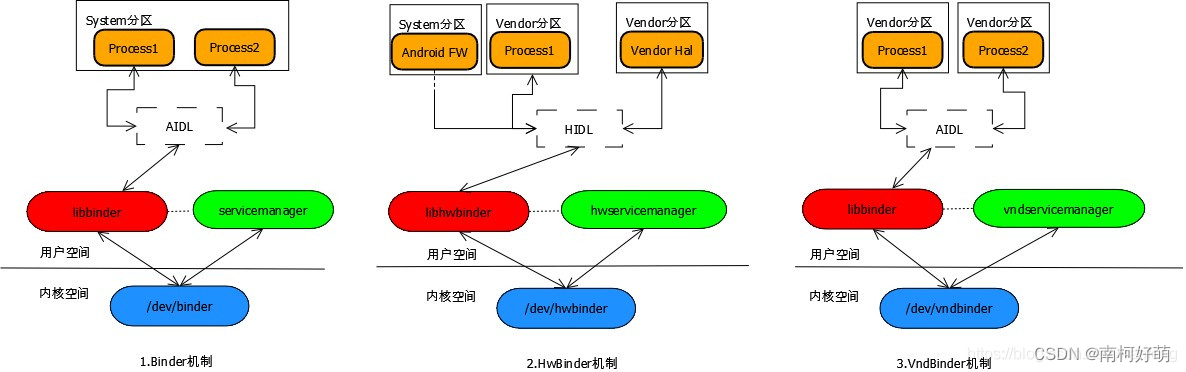
AOSP ~binder communication principle (I) - Overview

张平安:加快云上数字创新,共建产业智慧生态
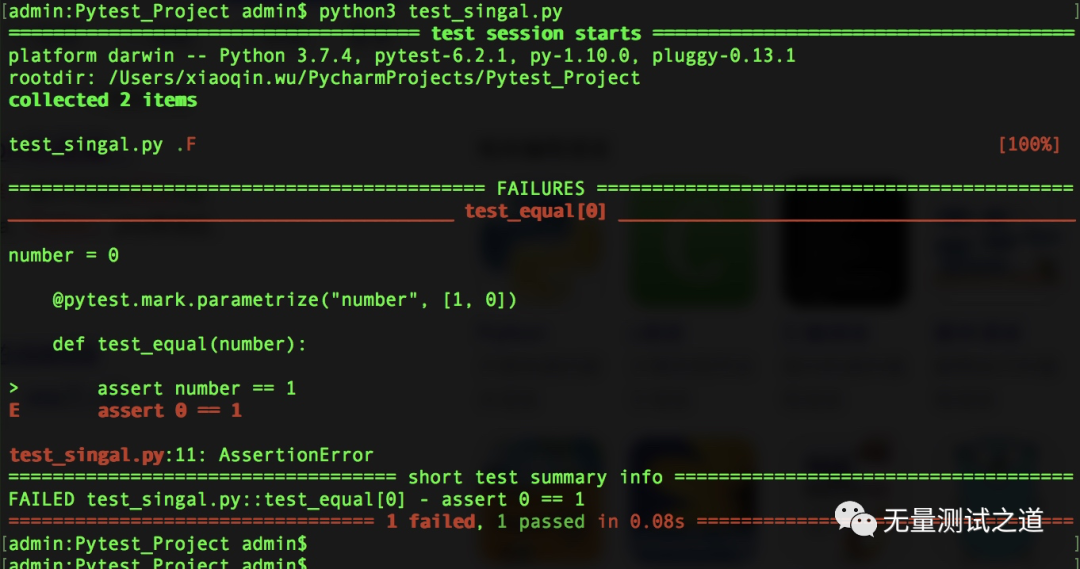
Pytest testing framework -- data driven

Digital innovation driven guide
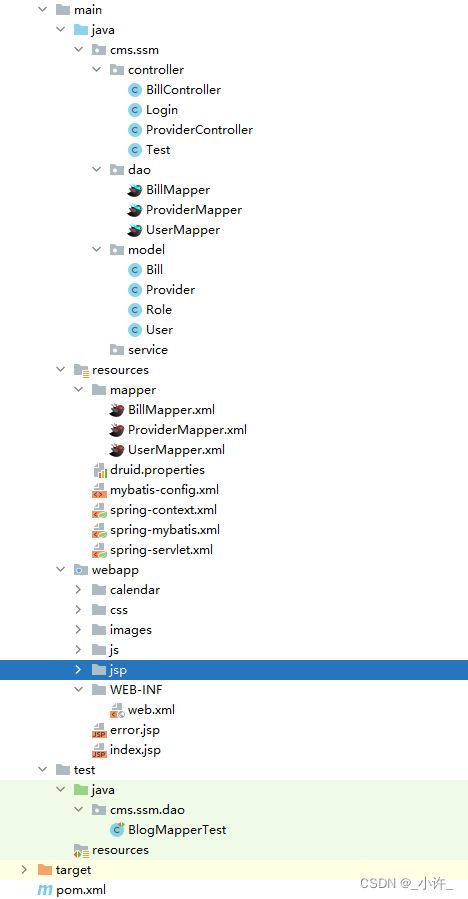
ssm框架的简单案例
随机推荐
Full link voltage test: the dispute between shadow database and shadow table
DFS, BFS and traversal search of Graphs
纪念下,我从CSDN搬家到博客园啦!
利用OPNET进行网络仿真时网络层协议(以QoS为例)的使用、配置及注意点
Where is NPDP product manager certification sacred?
The founder has a debt of 1billion. Let's start the class. Is it about to "end the class"?
实现网页内容可编辑
基于 hugging face 预训练模型的实体识别智能标注方案:生成doccano要求json格式
JSP setting header information export to excel
Most commonly used high number formula
QT simple layout box model with spring
Leetcode (417) -- Pacific Atlantic current problem
Zhang Ping'an: accelerate cloud digital innovation and jointly build an industrial smart ecosystem
“多模态”概念
Flink SQL 实现读写redis,并动态生成Hset key
Window scheduled tasks
Senior programmers must know and master. This article explains in detail the principle of MySQL master-slave synchronization, and recommends collecting
What changes will PMP certification bring?
EGR-20USCM接地故障继电器
Photo selector collectionview