当前位置:网站首页>Discrete mathematics: propositional symbolization of predicate logic
Discrete mathematics: propositional symbolization of predicate logic
2022-07-05 00:58:00 【Xiaobai Xiaozheng】
Individual words
- Individual constant or individual constant : Use x, y, z Express
- Individual variable or individual variable : Use a, b, c Express
- Individual domain or discourse : Value of individual argument
- Total individual domain : Everything in the universe
The predicate
- Concept : A word that indicates the nature of an individual or the relationship between them
- Illustrate with examples :A(x) Can mean x It's the students ,B(x,y) Can mean x Greater than y
quantifiers
- Full name quantifier ∀:∀x Represents all x
- There are quantifiers ∃:∃x Indicates that x
exercises
The individual domain is limited to (a) and (b) When the conditions , Symbolize the following proposition :
proposition :
(1) For any x, There are x2-5x+6=(x-2)(x-3).
(2) There is x, bring x+1=0.
Conditions :
(a) Individual domain D1 Is a set of natural numbers .
(b) Individual domain D2 Is a set of real numbers .
Explain : Make F(x):x2-5x+6=(x-2)(x-3),G(x):x+1=0
For conditions (a), Individual domain D1 After symbolization
(1) ∀xF(x), True proposition .
(2) ∀xG(x), False proposition , Natural number is greater than or equal to 0.
For conditions (b), Individual domain D2 After symbolization
(1) ∀xF(x), True proposition .
(2) ∀xG(x), True proposition .
Proposition symbolization
The basic formula
F(x):x Have the quality of F
G(x):x Have the quality of G
(1) There are properties in the individual domain F All individuals have properties G
Proposition symbolization :∀x(F(x)→G(x))
(2) There are properties in the individual domain F And nature G The individual of
Proposition symbolization :∃x(F(x)∧G(x))
Propositional symbolization steps
(1) Determine the scope of individual domain ( Human beings gather 、 Total individual domain …)
(2) Definite predicate (G(x):x Prime number 、F(x):x Born myopia …)
(3) Get the symbolic result of proposition
exercises
Not all rabbits run faster than turtles .
Explain :
(1) The individual domain is the total individual domain
(2)F(x):x It's a rabbit ,G(y):y It's a turtle
--------H(x,y):x Than y Run fast
(3)¬∀x(F(x)∧∀y(G(y)→H(x,y)))
边栏推荐
- URLs and URIs
- P4281 [ahoi2008] emergency assembly / gathering (LCA)
- [error reporting] "typeerror: cannot read properties of undefined (reading 'split')“
- ORB(Oriented FAST and Rotated BRIEF)
- PyTorch: In-place Operation
- Applet live + e-commerce, if you want to be a new retail e-commerce, use it!
- leetcode518,377
- Postman automatically fills headers
- The most complete regular practical guide of the whole network. You're welcome to take it away
- Detailed explanation of openharmony resource management
猜你喜欢

Daily question brushing record (13)
SAP ui5 application development tutorial 107 - trial version of SAP ui5 overflow toolbar container control introduction
SAP UI5 应用的主-从-从(Master-Detail-Detail)布局模式的实现步骤
Pycharm professional download and installation tutorial
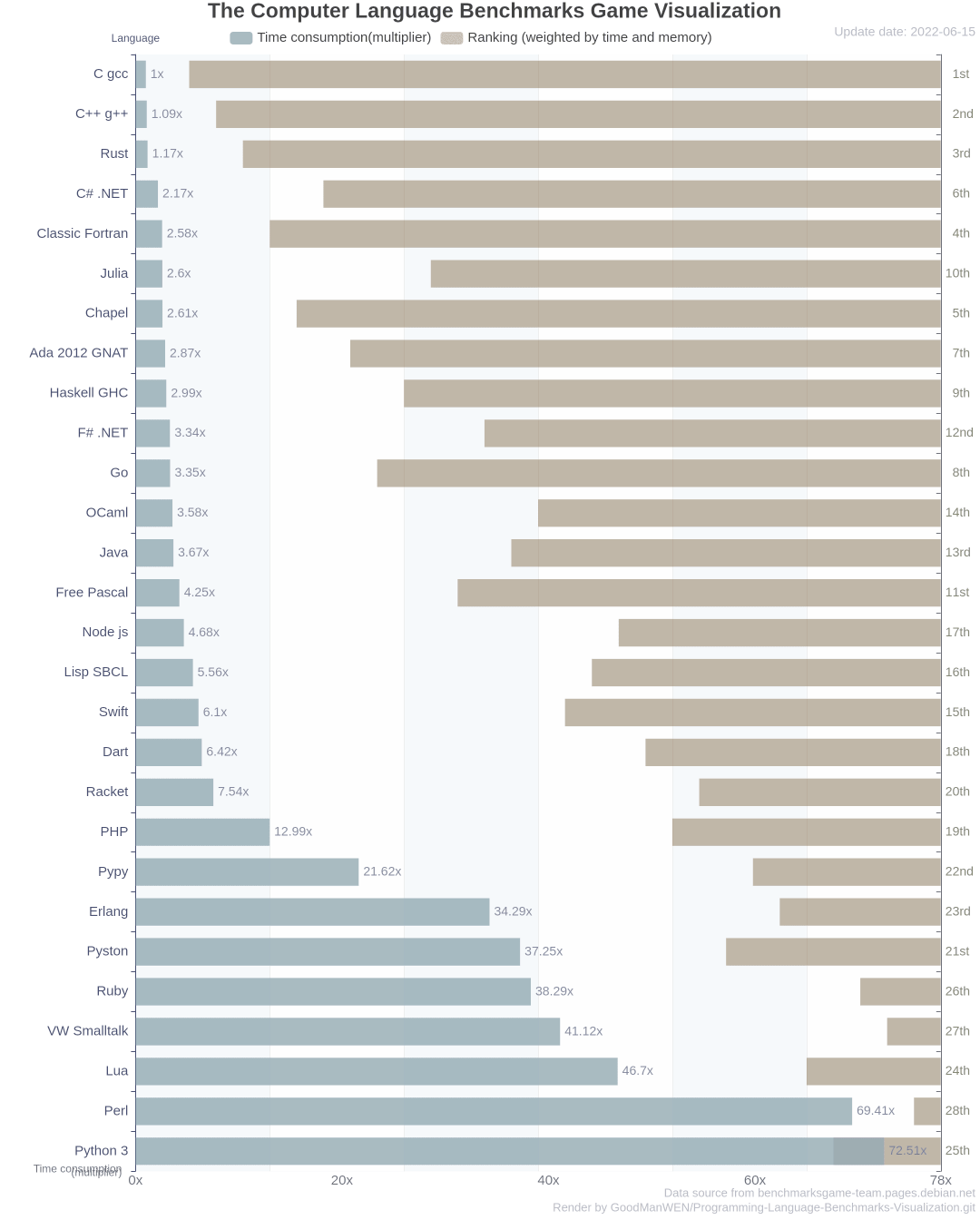
The performance of major mainstream programming languages is PK, and the results are unexpected

Chia Tai International Futures: what is the master account and how to open it?
Get to know ROS for the first time

Innovation leads the direction. Huawei Smart Life launches new products in the whole scene
College degree, what about 33 year old Baoma? I still sell and test, and my monthly income is 13K+
Several simplified forms of lambda expression
随机推荐
Check if this is null - checking if this is null
Acwing164. Accessibility Statistics (topological sorting +bitset)
Detailed explanation of multi-mode input event distribution mechanism
There is a new Post-00 exam king in the testing department. I really can't do it in my old age. I have
Ruby tutorial
FEG founder rox:smartdefi will be the benchmark of the entire decentralized financial market
“薪资倒挂”、“毕业生平替” 这些现象说明测试行业已经...
Which financial products with stable income are good
1189. Maximum number of "balloons"
Arbitrum: two-dimensional cost
Hisilicon 3559 universal platform construction: YUV422 pit stepping record
107. SAP UI5 OverflowToolbar 容器控件以及 resize 事件处理的一些细节介绍
Parameter passing mechanism of member methods
Deux nombres se remplacent
Relationship between classes and objects
leetcode518,377
"Upside down salary", "equal replacement of graduates" these phenomena show that the testing industry has
[wave modeling 2] three dimensional wave modeling and wave generator modeling matlab simulation
Safety learning week4
[pure tone hearing test] pure tone hearing test system based on MATLAB