当前位置:网站首页>LeetCode·85.最大矩形·单调栈
LeetCode·85.最大矩形·单调栈
2022-08-04 15:51:00 【小迅想变强】
链接:https://leetcode.cn/problems/maximal-rectangle/solution/by-xun-ge-v-zhxr/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
题目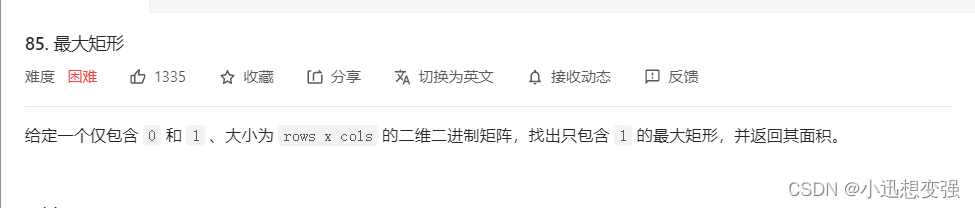
示例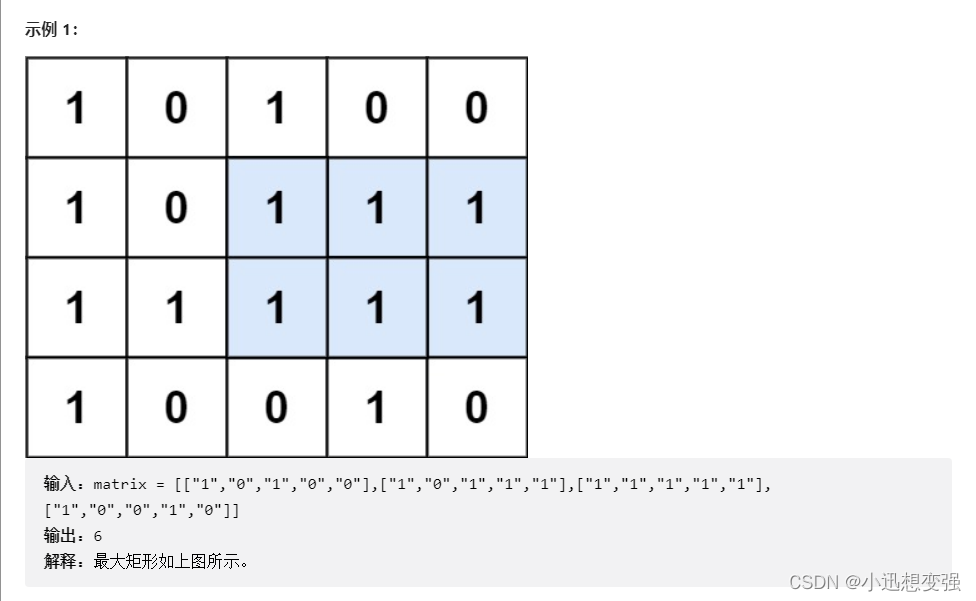
思路
解题思路
本题与84题思路大体相同,是84题的进阶题,可以移步先看看84题
84.题解
84题是在一维空间求最大矩形,本题是在二维空间求矩形,思路一样,可以将二维空间转换为一维空间与84题一模一样
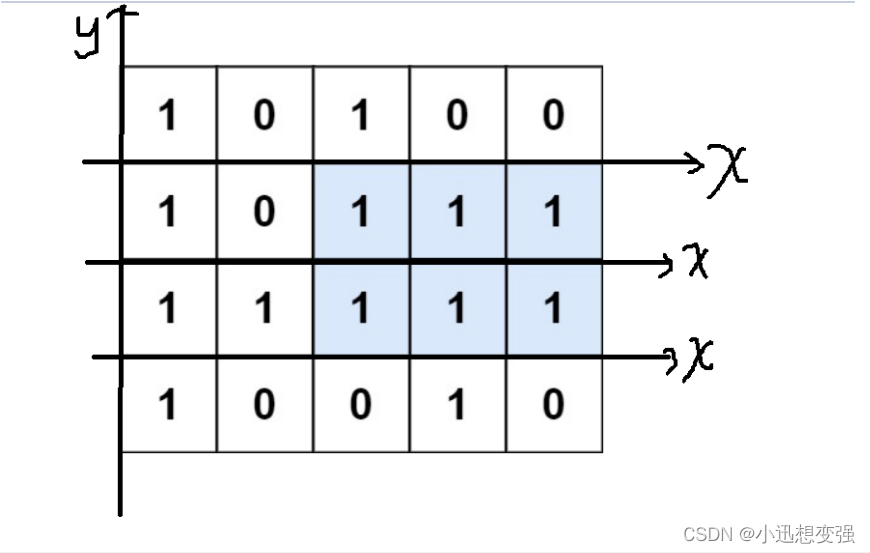
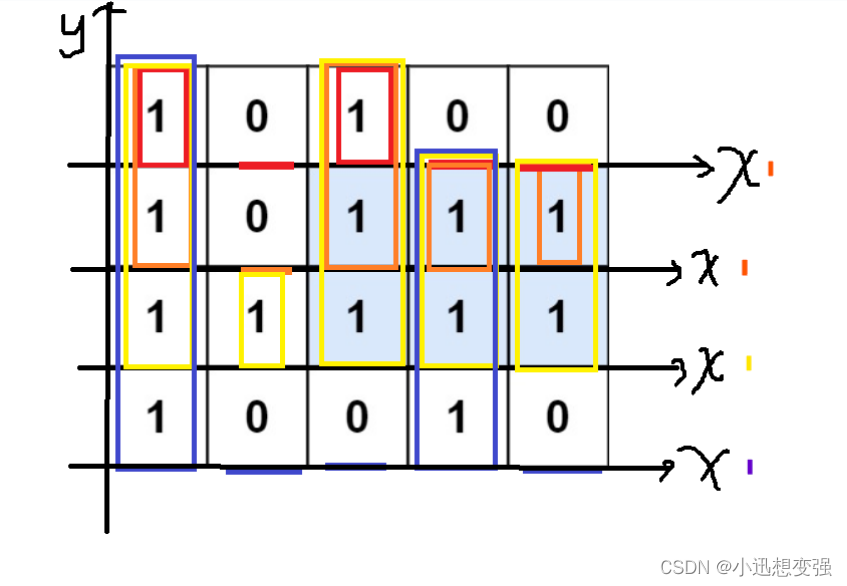
暴力求解:
我们按照题目给定要求,枚举数组每一个元素,将对应的高和宽相乘组成面积,保存最大面积即可,因为给定为字符串,所以先对其进行处理,转换为二维整形数组,同时求其在Y方向的高
单调栈+哨兵:
通过暴力解法,时间消耗非常大
那么可以利用递增栈优化暴力暴力求解的过程
- 当元素大于栈顶元素时,入栈
- 当元素小于栈顶元素时,维护栈的递增性,将小于当前元素的栈顶元素弹出,并计算面积
在上面递增栈中,我们总是需要判断当前元素是否为最后元素或者为栈顶元素,很麻烦,那么可以在数组前后加上两个哨兵,充当坏点,在实际计算中不影响结果,但是简化我们的逻辑,正如我们高中或者初中学过的辅助线或者凑配法都是差不多的思路
具体实现看代码,注释超级详细
代码
暴力求解:
int maximalRectangle(char** matrix, int matrixSize, int* matrixColSize){
int dp[matrixSize][matrixColSize[0]];
memset(dp, 0, sizeof(dp));
for(int i = 0; i < matrixSize; i++)//计算对应高度
{
for(int j = 0; j < matrixColSize[0]; j++)
{
if(matrix[i][j] == '1')
{
dp[i][j] = (i == 0 ? 0 : dp[i-1][j])+1;
}
}
}
int max = 0;
for(int i = 0; i < matrixSize; i++)
{
for(int j = 0; j < matrixColSize[0]; j++)//计算每一个点能构成的最大面积
{
if(matrix[i][j] == '0')
{
continue;
}
int min = dp[i][j];//高
for(int k = j; k >= 0; k--)
{
if(matrix[i][k] == '0')
{
break;
}
min = fmin(min, dp[i][k]);//每次保存最小高
max = fmax(max, (j - k + 1) * min);
}
}
}
return max;
}
作者:xun-ge-v
链接:https://leetcode.cn/problems/maximal-rectangle/solution/by-xun-ge-v-zhxr/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。单调栈+哨兵:
int maximalRectangle(char** matrix, int matrixSize, int* matrixColSize){
int dp[matrixSize][matrixColSize[0] + 2];//添加哨兵
memset(dp, 0, sizeof(dp));//初始化
for(int i = 0; i < matrixSize; i++)//计算对应高度
{
for(int j = 0; j < matrixColSize[0]; j++)
{
if(matrix[i][j] == '1')
{
dp[i][j+1] = (i == 0 ? 0 : dp[i-1][j+1])+1;
}
}
}
int max = 0;
for(int i = 0; i < matrixSize; i++)//转为一维,
{
int stack[matrixColSize[0]+2];//单调栈解法
int top = -1;
stack[++top] = 0;
for(int j = 1; j < matrixColSize[0]+2; j++)
{
while(dp[i][j] < dp[i][stack[top]])
{
max = fmax(max, (j - stack[top-1] - 1) * dp[i][stack[top]]);
--top;
}
stack[++top] = j;
}
}
return max;
}
作者:xun-ge-v
链接:https://leetcode.cn/problems/maximal-rectangle/solution/by-xun-ge-v-zhxr/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。边栏推荐
猜你喜欢

字节API鉴权方法
In action: 10 ways to implement delayed tasks, with code!

我说MySQL联合索引遵循最左前缀匹配原则,面试官让我回去等通知

图解 SQL,这也太形象了吧!
什么是 DevOps?看这一篇就够了!
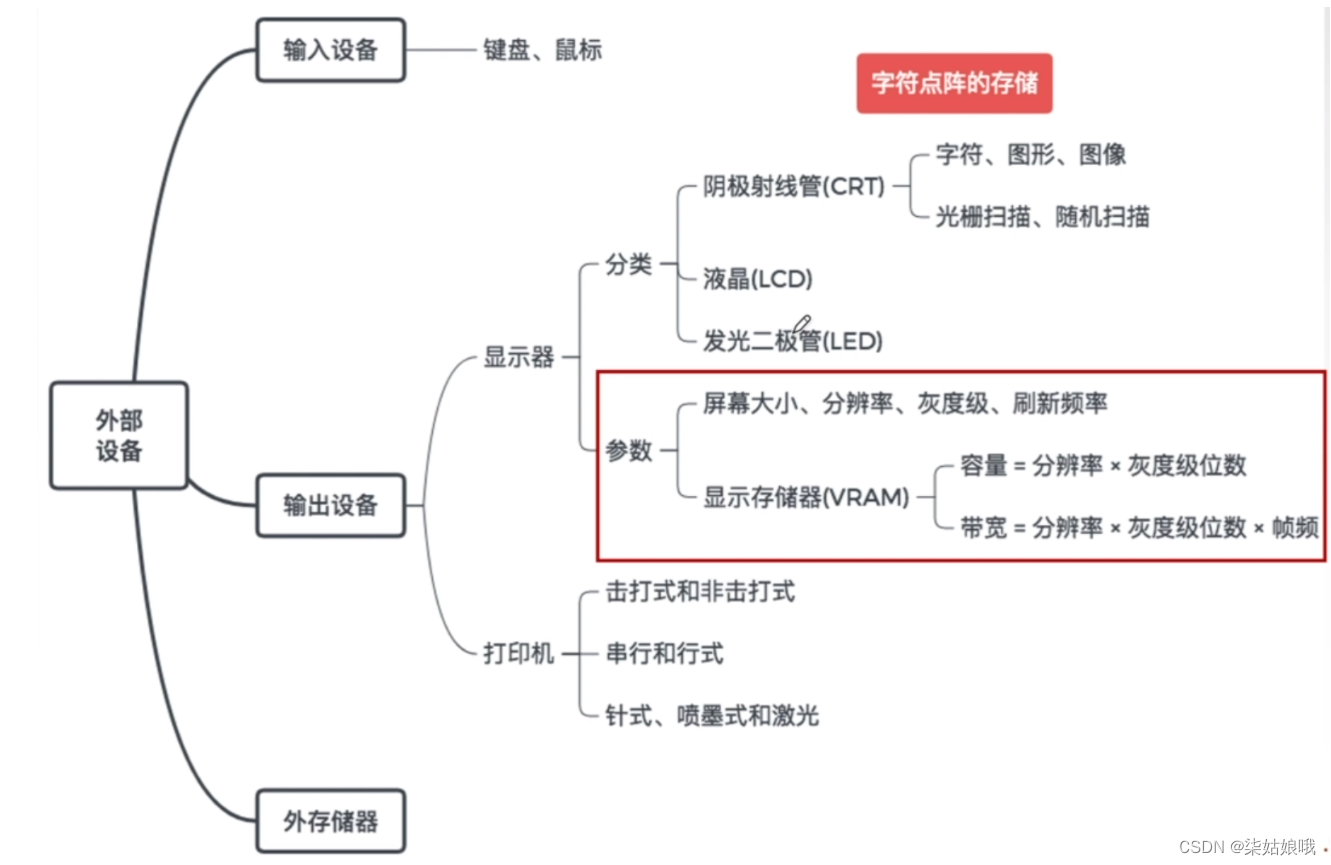
07-输入输出系统
Byte、Short、Integer、Long内部缓存类的对比与源码分析
【已解决】allure无法生成json文件和AttributeError: module ‘allure‘ has no attribute ‘severity_level‘

NUS颜水成等发布首篇《深度长尾学习》综述

【TA-霜狼_may-《百人计划》】美术2.7 Metallic 与 Speculer流程
随机推荐
附加:自定义注解(参数校验注解);(写的不好,别看…)
花了半个月,终于把一线大厂高频面试题做成合集了
Roslyn 在 msbuild 的 target 判断文件存在
Go Go 简单的很,标准库之 fmt 包的一键入门
【二叉树】根据描述创建二叉树
H5 之 文件流转base64下载
进程间通信方式
OGG判断mgr状态并自动启动脚本
吴恩达机器学习[13]-支持向量机
爬虫小白笔记(昨天的对于注意解析数据的补充)
面了三十个人,说说真实感受
DocuWare Platform - Content Services and Workflow Automation Platform for Document Management (Part 1)
解决dataset.mnist无法加载进去的情况
Tinymce plugins [Tinymce 扩展插件集合]
成功 解决 @keyup.enter=“search()“ 在el-input 组件中不生效的问题
图解 SQL,这也太形象了吧!
Request method ‘POST‘ not supported。 Failed to load resource: net::ERR_FAILED
界面组件DevExpress ASP.NET Core v22.1 - 增强数据导出功能
What are the useful IT asset management platforms?
ICDE‘22推荐系统论文之Research篇