当前位置:网站首页>Matlab dichotomy to find the optimal solution
Matlab dichotomy to find the optimal solution
2022-07-03 09:16:00 【Fingering 13】
MATLAB Dichotomy to find the optimal solution
【 Vegetable dog bb】emm… The principle is quite simple , There should be nothing you don't understand . Is to give a function f And interval [a,b] And accuracy esp, Take the derivative of the intermediate value of the interval , Less than 0 Just assign the intermediate value to a, Greater than 0 Just assign the intermediate value to b. If the derivative equals 0 perhaps b-a The value is less than esp No longer judge , The intermediate value is the abscissa of the optimal solution .
No grinding , Look at the code or :
Here are some .
function [k,y]=erfenfa1(f,a,b,esp)
syms x;
% f Is the function given a,b For the given interval ,eps For accuracy
% Return value [k,y] Is the horizontal and vertical coordinates of the optimal solution
while b-a > esp
% Find out in a,b The derivative of the intermediate point
zhong = (b+a)/2;
dao = subs(diff(f),x,zhong);
% If the reciprocal is 0, be a,b In the middle zhong Is the abscissa of the optimal solution
if dao == 0
k=zhong;
y = subs(f,x,zhong);
break;
else
% The derivative is less than 0 take zhong Assign a value to a, Greater than 0 Assign to b
if(dao<0)
a = zhong;
else
b = zhong;
end
end
% When b-a Less than esp when , take a,b The midpoint is the abscissa of the optimal solution ,y Vertical coordinates
if b-a<=esp
k =(b+a)/2;
y = subs(f,x,k);
end
end
emm… Look at a simple test case :
>> clear
>> syms x;
f = x^2 + 2*x -1;
[x,y] = erfenfa1(f,-2,0,0.1);
>> [x,y]
ans =
[ -1, -2]
emm… One more piece ,,, Give me a compliment and I'll show you again , how ..( Manually cheat like )
Bye-bye , Hey .
边栏推荐
- Wonderful review | i/o extended 2022 activity dry goods sharing
- PIC16F648A-E/SS PIC16 8位 微控制器,7KB(4Kx14)
- Uc/os self-study from 0
- 数字化管理中台+低代码,JNPF开启企业数字化转型的新引擎
- AcWing 788. Number of pairs in reverse order
- LeetCode 871. 最低加油次数
- What are the stages of traditional enterprise digital transformation?
- In the digital transformation, what problems will occur in enterprise equipment management? Jnpf may be the "optimal solution"
- LeetCode 532. K-diff number pairs in array
- On February 14, 2022, learn the imitation Niuke project - develop the registration function
猜你喜欢

On February 14, 2022, learn the imitation Niuke project - develop the registration function

LeetCode 75. Color classification
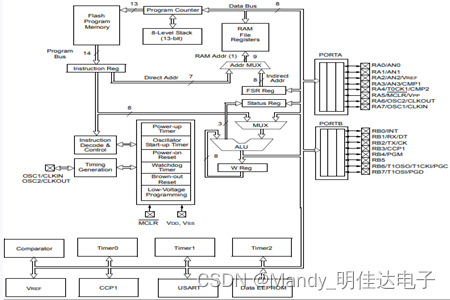
PIC16F648A-E/SS PIC16 8位 微控制器,7KB(4Kx14)
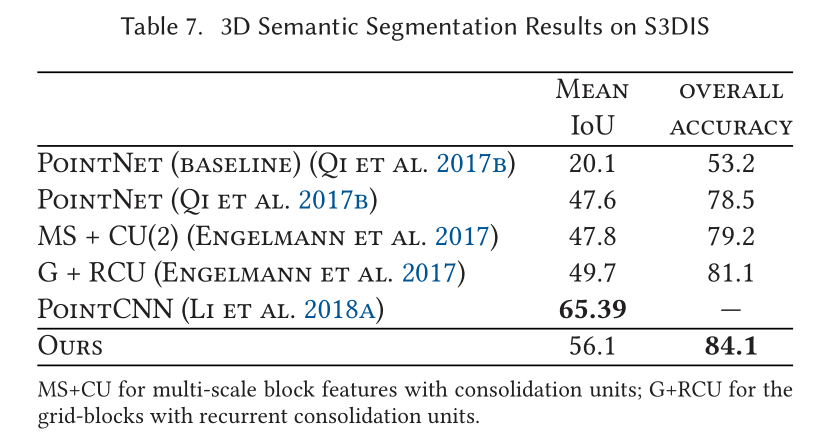
【点云处理之论文狂读经典版14】—— Dynamic Graph CNN for Learning on Point Clouds

【点云处理之论文狂读前沿版8】—— Pointview-GCN: 3D Shape Classification With Multi-View Point Clouds
传统办公模式的“助推器”,搭建OA办公系统,原来就这么简单!

LeetCode 57. 插入区间

LeetCode 241. Design priorities for operational expressions

2022-1-6 Niuke net brush sword finger offer

Basic knowledge of network security
随机推荐
教育信息化步入2.0,看看JNPF如何帮助教师减负,提高效率?
低代码前景可期,JNPF灵活易用,用智能定义新型办公模式
2022-2-14 learning the imitation Niuke project - send email
Too many open files solution
LeetCode 30. 串联所有单词的子串
LeetCode 508. 出现次数最多的子树元素和
剑指 Offer II 091. 粉刷房子
LeetCode 535. TinyURL 的加密与解密
数位统计DP AcWing 338. 计数问题
Digital management medium + low code, jnpf opens a new engine for enterprise digital transformation
Discussion on enterprise informatization construction
Pic16f648a-e/ss PIC16 8-bit microcontroller, 7KB (4kx14)
【Kotlin学习】类、对象和接口——带非默认构造方法或属性的类、数据类和类委托、object关键字
2022-2-14 learning xiangniuke project - generate verification code
Linxu learning (4) -- Yum and apt commands
Summary of methods for counting the number of file lines in shell scripts
【点云处理之论文狂读经典版13】—— Adaptive Graph Convolutional Neural Networks
求组合数 AcWing 885. 求组合数 I
Jenkins learning (I) -- Jenkins installation
AcWing 787. Merge sort (template)