Bernoulli distribution, binomial distribution and Poisson distribution, and the relationship between maximum likelihood (incomplete)

First of all, Bernoulli test

Bernoulli distribution

Bernoulli experiment is about the following event ： In the life , There are only two possibilities for some events to happen , Happen or not （ Or success or failure ）, These events can be called Bernoulli experiment .

Probability distribution of Bernoulli test It is called Bernoulli distribution （ Two point distribution 、0-1 Distribution ）, If the probability of success is recorded as p, Then the failure probability is q=1-p, be ：

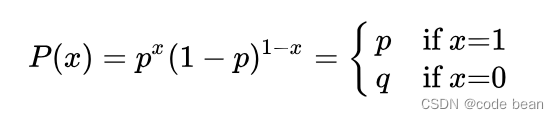
The binomial distribution

Suppose a certain experiment is Bernoulli experiment . Conduct n This is an experiment like this , succeed x Time , Failed n-x. Binomial distribution holds that ： The probability of this happening can be calculated by the following formula ：

The probability quality function of binomial distribution can be abbreviated as X~B(n,p).

actually , When n = 1 when , The binomial distribution is ​ ​ Bernoulli distribution ​​. This is the relationship between binomial distribution and Bernoulli distribution .

So here we can see , Binomial distribution is a histogram of discrete distribution .X The axis is the number of successes ,Y The axis corresponds to success n Number probability value . 

  As the number of experiments increases , We will get a histogram similar to the normal distribution .

An interesting example （ On binomial distribution ）

  What he will do is if you go shopping in JD , You want to buy a bike , Then I searched three stores , The first store has a total of 10 comments , It's all good reviews . The second ,50 comments ,96% The high praise , A third ,200 comments 96% The high praise . Which store should I choose to buy . Here I assume a premise , Suppose the bike mass OK Is the probability that x（ quality NG Is the probability that 1-x）, When buyers buy OK Your bike will give you good reviews , Otherwise, bad comments .

Look at the first one ,10 comments , It's all good reviews . Then it can be said that the yield rate of the first bicycle is 100% Do you ？ Not necessarily . We assume that the yield of the first bicycle is 0.95. Then each extraction 10 Bicycles are OK The probability of is actually quite high （ amount to 10 Every customer buys OK The probability of cycling ）.

The figure below shows , If the yield of bicycle is 0.95, Every time 10 car , Separate extraction 7,8,9,10 The car is OK Probability .

  in other words , although 10 comments , It's all good reviews . But bicycle OK The rate is also uncertain . But according to this binomial distribution , You said that the good product rate of this store is 0.95 about , It feels OK . Generally speaking, there are too few samples , There are many possible situations .

in other words , If the yield is determined before , You can see the probability of favorable comment rate

   such as , If the yield is 0.95, So if there is 50 comments , Among them is 48 The probability of a positive comment is 0.26110（ appear 47 Or 49 Good reviews are also 0.2 above ）

So in turn , If we know a positive binomial distribution , Can we introduce the most likely yield ？ In fact, the distribution and yield s There is a corresponding relationship .

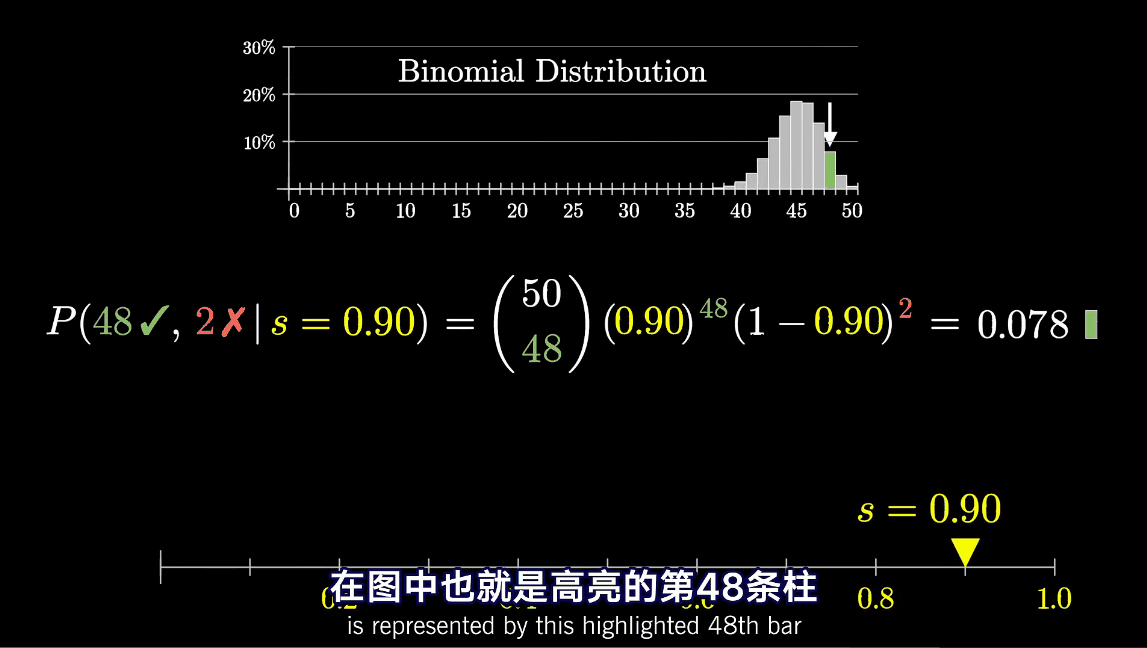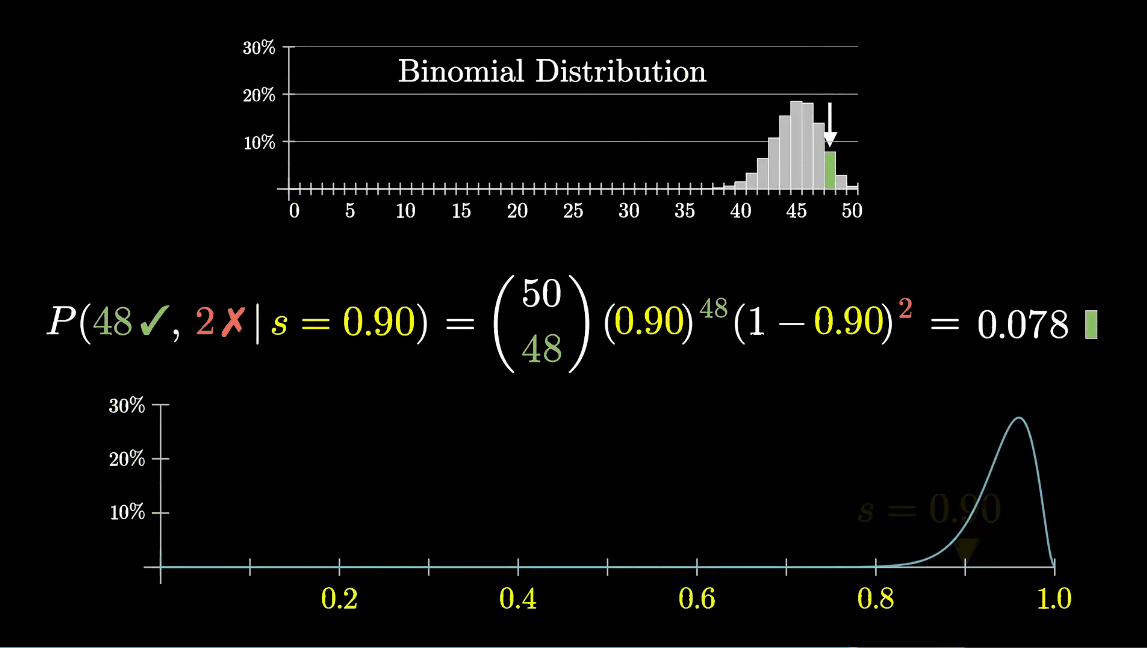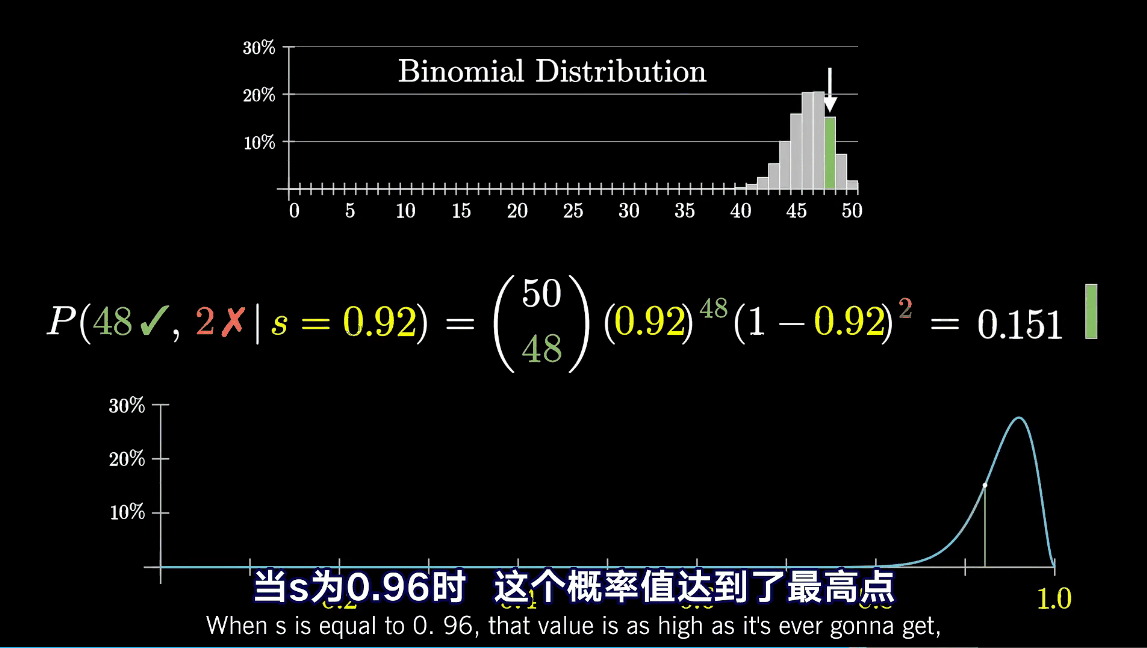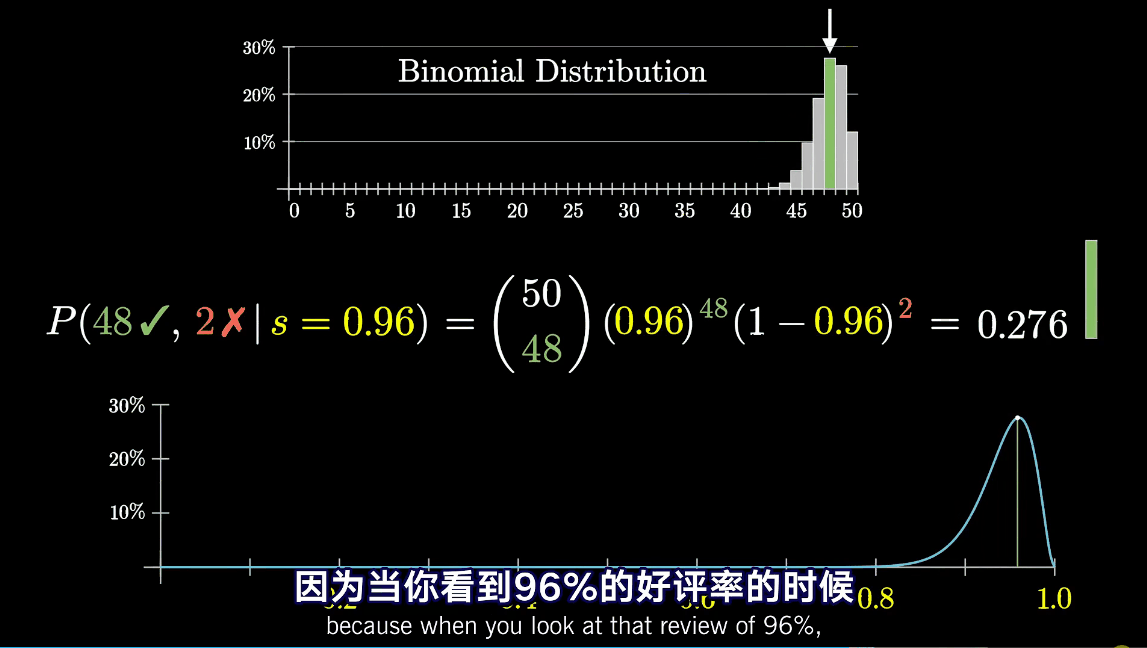
  This figure shows , When s by 0.96 When ,50 Comments appear 48 The probability of favorable comments is the greatest .

Stage summary ： In this case , I think of , Prior probability , Posterior probability , maximum likelihood （ Deduce the probability model according to the established facts ）, Even related to Poisson distribution .

These also seem to be related to naive Bayes , That's all for the discussion in this part , Later, slowly complete the knowledge system .

  Poisson distribution

Firstly, Poisson distribution is a special form of binomial distribution , When the binomial distribution formula p Approach 0（ Very small ）, The number of experiments approaches infinity , And n*p Equal to a constant , We will get Poisson distribution . In Poisson distribution “ Enter into ” In fact, it is in the binomial distribution n*p.

Three conditions need to be satisfied for the event to apply Poisson distribution ：

1 This event is a small probability event

2 Events are independent of each other

3 The probability of the event is stable

Divide a certain time infinitely , Until an event occurs at most once in time . Then this period of time I call it the unit time of Poisson distribution .

subject 1： At present, one minute has come 3 Vehicles , Please come in a minute 5 The probability of a car ？

  When “ Enter into ” After determining , This image is determined , probability P With K Change by change . In binomial distribution, we need to know n and p

This “ Enter into ” The meaning is , The average occurrence rate of random events in unit time （ That's right is np 了 np The meaning of is expectation / mean value ）

subject 2： Xinhua Bookstore , Weekly sales 4 This Xinhua Dictionary , How many Xinhua dictionaries should the boss prepare ？（ Hang in the air ）

---

Reference material ：

Statistics and quality 026 - Bernoulli test and probability equation Binomial distribution Expectation and variance _ Bili, Bili _bilibili 

Probability of probability , The first part -- The binomial distribution _ Bili, Bili _bilibili

How did Poisson distribution come from ？ How to use ？_ Bili, Bili _bilibili