当前位置:网站首页>【ACWing】230. 排列计数
【ACWing】230. 排列计数
2022-08-01 23:47:00 【记录算法题解】
题目地址:
https://www.acwing.com/problem/content/description/232/
求有多少种长度为 n n n的序列 A A A,满足以下条件: 1 ∼ n 1∼n 1∼n这 n n n个数在序列中各出现了一次。若第 i i i个数 A [ i ] A[i] A[i]的值为 i i i,则称 i i i是稳定的,序列恰好有 m m m个数是稳定的。由于满足条件的序列可能很多,所以请你将序列数对 1 0 9 + 7 10^9+7 109+7取模后输出。
输入格式:
第一行一个数 T T T,表示有 T T T组数据。
接下来 T T T行,每行两个整数 n n n、 m m m。
输出格式:
输出 T T T行,每行一个整数,表示求出的序列数对 1 0 9 + 7 10^9+7 109+7取模后的值。
数据范围:
T ≤ 500000 , n ≤ 1000000 , m ≤ 1000000 T≤500000,n≤1000000,m≤1000000 T≤500000,n≤1000000,m≤1000000
首先, k k k个数的错排问题的解 f [ k ] f[k] f[k]满足 f [ k ] = ( k − 1 ) ( f [ k − 1 ] + f [ k − 2 ] ) , f [ 1 ] = 0 , f [ 2 ] = 1 f[k]=(k-1)(f[k-1]+f[k-2]),f[1]=0,f[2]=1 f[k]=(k−1)(f[k−1]+f[k−2]),f[1]=0,f[2]=1。参考https://blog.csdn.net/qq_46105170/article/details/125235949。那么本题可以分步骤,先取 m m m个数,方案为 ( n m ) n\choose m (mn)个,剩下的 n − m n-m n−m个数做错排即可。所以答案就是 ( n m ) f [ n − m ] {n\choose m} f[n-m] (mn)f[n−m] f f f值可以打个表,阶乘的值也可以打个表。由于 ( n m ) = n ! m ! ( n − m ) ! {n\choose m}=\frac{n!}{m!(n-m)!} (mn)=m!(n−m)!n!,而 p = 1 0 9 + 7 p=10^9+7 p=109+7是个素数,从而 a a a模 p p p的逆元可以用费马小定理和快速幂来做。费马小定理为,若 p p p为素数, ( a , p ) = 1 (a,p)=1 (a,p)=1,则 a p − 1 ≡ a a p − 2 ≡ 1 ( m o d p ) a^{p-1}\equiv aa^{p-2}\equiv1(\mod p) ap−1≡aap−2≡1(modp),从而 a a a的逆元为 a p − 2 a^{p-2} ap−2。逆元可以用记忆化避免重复计算。代码如下:
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e6 + 10, P = 1e9 + 7;
long fac[N], f[N], inv[N];
int n, m;
long fast_pow(long x, int p) {
long res = 1;
while (p) {
if (p & 1) res = res * x % P;
x = x * x % P;
p >>= 1;
}
return res;
}
long inverse(int i) {
if (~inv[i]) return inv[i];
return inv[i] = fast_pow(fac[i], P - 2);
}
long comb(int n, int m) {
return fac[n] * inverse(m) % P * inverse(n - m) % P;
}
int main() {
memset(inv, -1, sizeof inv);
f[0] = 1, f[1] = 0;
fac[0] = fac[1] = 1;
for (int i = 2; i < N; i++) {
f[i] = (i - 1) * (f[i - 1] + f[i - 2]) % P;
fac[i] = fac[i - 1] * i % P;
}
int T;
scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &m);
printf("%ld\n", comb(n, m) * f[n - m] % P);
}
}
预处理时间复杂度 O ( N ) O(N) O(N)( N N N为 n n n数据范围),每次询问时间 O ( log P ) O(\log P) O(logP), P = 1 0 9 + 7 P=10^9+7 P=109+7。
边栏推荐
- numpy.around
- Getting started with IDEA is enough to read this article
- 怎样做才能让这条SQL变成一条危险的SQL?
- 分享一份接口测试项目(非常值得练手)
- How to better understand and do a good job?
- cdh6 opens oozieWeb page, Oozie web console is disabled.
- Additional Features for Scripting
- CDH6的Hue打开出现‘ascii‘ codec can‘t encode characters
- numpy.hstack
- 12306抢票,极限并发带来的思考?
猜你喜欢
![[C language advanced] file operation (2)](/img/4d/49d9603aeed16f1600d69179477eb3.png)
[C language advanced] file operation (2)

With a monthly salary of 12K, the butterfly changed to a new one and moved forward bravely - she doubled her monthly salary through the career change test~
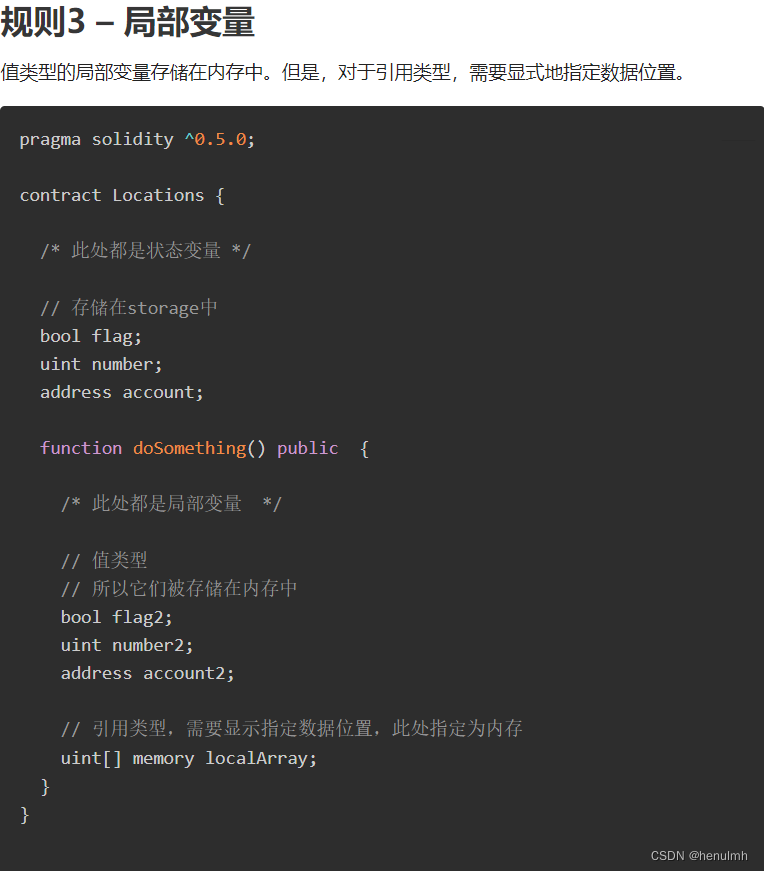
solidity
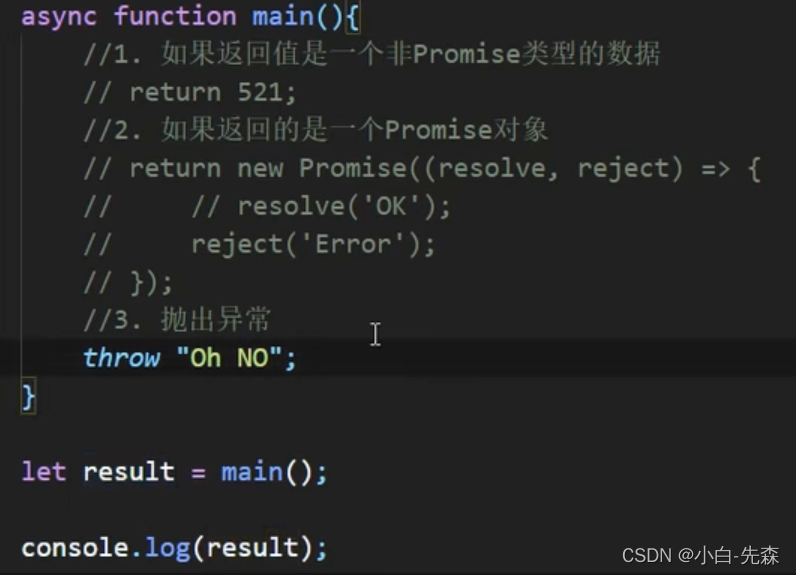
async和await用法介绍

【C语言进阶】文件操作(二)

企业防护墙管理,有什么防火墙管理工具?

经典文献阅读之--DLO

多御安全浏览器android版更新至1.7,改进加密协议

C语言——分支语句和循环语句
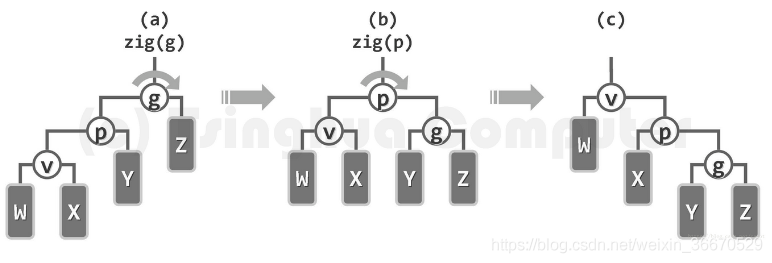
伸展树的特性及实现
随机推荐
Quartus uses tcl files to quickly configure pins
Additional Features for Scripting
A brief analysis of mobile APP security testing in software testing, shared by a third-party software testing agency in Beijing
YOLO等目标检测模型的非极大值抑制NMS和评价指标(Acc, Precision, Recall, AP, mAP, RoI)、YOLOv5中[email protected]与
6134. Find the closest node to the given two nodes - force double hundred code
Work for 5 years, test case design is bad?To look at the big case design summary
ansible模块--copy模块
Data Organization --- Chapter 5 Trees and Binary Trees --- The Concept of Binary Trees --- Application Questions
Getting started with IDEA is enough to read this article
Solve the port to take up
Leetcode 129求根节点到叶节点数字之和、104二叉树的最大深度、8字符串转换整数(atoi)、82删除排序链表中的重复元素II、204二分查找、94二叉树的中序遍历、144二叉树的前序遍历
【图像融合】基于加权和金字塔实现图像融合附matlab代码
@Transactional注解在类上还是接口上使用,哪种方式更好?
solidity
获取小猪民宿(短租)数据
@Transactional 注解使用详解
机器学习文本分类
Chapter 12 End-User Task As Shell Scripts
经典文献阅读之--DLO
根本上解决mysql启动失败问题Job for mysqld.service failed because the control process exited with error code