当前位置:网站首页>Sword finger offer10- I. Fibonacci sequence
Sword finger offer10- I. Fibonacci sequence
2022-07-03 12:27:00 【Wu Liuqi】
The finger of the sword Offer10- I. Fibonacci sequence
Title Description
Write a function , Input n , Fibonacci, please (Fibonacci) The number of the sequence n term ( namely F(N)). Fibonacci series is defined as follows :
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), among N > 1.
The Fibonacci series is composed of 0 and 1 Start , The Fibonacci number after that is the sum of the two numbers before .
The answer needs to be modelled 1e9+7(1000000007), If the initial result of calculation is :1000000008, Please return 1.
Example 1:
Input :n = 2
Output :1
Example 2:
Input :n = 5
Output :5
Tips :
0 <= n <= 100
JAVA Code
One 、 Recursive method ( Time limit exceeded )
class Solution {
public int fib(int n) {
if(n0){
return 0;
}
if(n1){
return 1;
}
return fib(n-1)+fib(n-2);
}
}
Two 、 Array helper ( Dynamic programming dp)
class Solution {
public int fib(int n) {
final int MOD = 1000000007;
int[] result = new int[100000];
result[0] = 0;
result[1] = 1;
for(int i = 2;i<=n;i++){
result[i] = (result[i-1]+result[i-2])%MOD;
}
return result[n];
}
}

No array helper is required ( Dynamic programming dp)
It can also be like the official , Do not use array assignment , It is also possible to calculate directly .
class Solution {
public int fib(int n) {
final int MOD = 1000000007;
if(n==0||n==1) return n;
int num1 = 0,num2 =0,sum = 1;
for(int i = 2;i<=n;i++){
num1 = num2;
num2 = sum;
sum = (num1 + num2) % MOD;
}
return sum;
}
}

Official methods : Matrix fast power
Algorithm design idea :

class Solution {
static final int MOD = 1000000007;
public int fib(int n) {
if (n < 2) {
return n;
}
int[][] q = {
{
1, 1}, {
1, 0}};
int[][] res = pow(q, n - 1);
return res[0][0];
}
// Matrix n Power multiplication
public int[][] pow(int[][] a, int n) {
// Initialize to unit matrix , Store the calculation results
int[][] ret = {
{
1, 0}, {
0, 1}};
// We calculate the even digits directly a*a, This is equivalent to halving the scale
// When there are odd digits , We will extract the preserved res Multiply with odd digits .-> Odd number * Even power multiplication
// This part is more abstract , Remember that power multiplication can reduce the size of the algorithm
while (n > 0) {
// Judge whether it is an odd number n%2==1
if ((n & 1) == 1) {
ret = multiply(ret, a);
}
// amount to n = n/2
n >>= 1;
a = multiply(a, a);
}
return ret;
}
// Multiplication method of two two-dimensional matrices
public int[][] multiply(int[][] a, int[][] b) {
// Store the multiplied result
int[][] c = new int[2][2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
c[i][j] = (int) (((long) a[i][0] * b[0][j] + (long) a[i][1] * b[1][j]) % MOD);
}
}
return c;
}
}
Time complexity O(logn), Spatial complexity O(1)
summary : Matrix fast power
Matrix fast power : Matrix n Power fast multiplication
Summary tools : Apply to any matrix n Power solution in progress
// Matrix n Power multiplication (n Power multiplication can apply this idea )
public int[][] pow(int[][] a, int n) {
// Initialize to unit matrix , Store the calculation results
int[][] ret = {
{
1, 0}, {
0, 1}};
// We calculate the even digits directly a*a, This is equivalent to halving the scale
// When there are odd digits , We will extract the preserved res Multiply with odd digits .-> Odd number * Even power multiplication
// This part is more abstract , Remember that power multiplication can reduce the size of the algorithm
while (n > 0) {
// Judge whether it is an odd number n%2==1
if ((n & 1) == 1) {
ret = multiply(ret, a);
}
// amount to n = n/2
n >>= 1;
a = multiply(a, a);
}
return ret;
}
// Multiplication method of two two-dimensional matrices
public int[][] multiply(int[][] a, int[][] b) {
// Store the multiplied result
int[][] c = new int[2][2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
c[i][j] = (int) (((long) a[i][0] * b[0][j] + (long) a[i][1] * b[1][j]) % MOD);
}
}
return c;
}
边栏推荐
- 2020-09_ Shell Programming Notes
- Shell: basic learning
- (construction notes) learn the specific technology of how to design reusable software entities from three levels: class, API and framework
- Redis
- Socket TCP for network communication (I)
- 242. Effective letter heteronyms
- Kubernetes three dozen probes and probe mode
- New features of ES6
- Applet wxss introduction
- Qt+vtk+occt reading iges/step model
猜你喜欢

【mysql专项】读锁和写锁

shardingSphere分库分表<3>
剑指Offer07. 重建二叉树

使用BLoC 构建 Flutter的页面实例
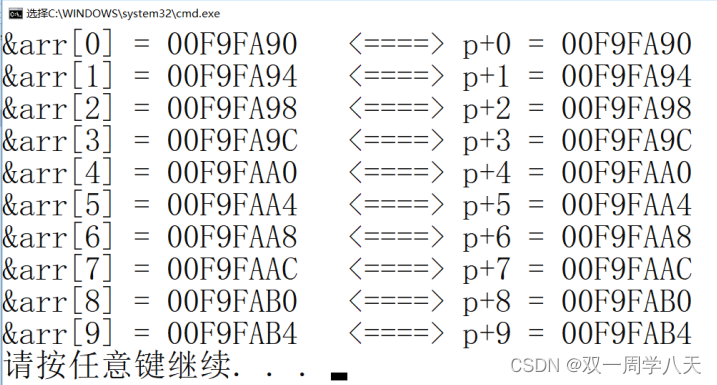
4000 word super detailed pointer

OpenGL index cache object EBO and lineweight mode

Itext7 uses iexternalsignature container for signature and signature verification

QT OpenGL texture map

Flutter 退出登录二次确认怎么做才更优雅?
Shutter: overview of shutter architecture (excerpt)
随机推荐
regular expression
Shardingsphere sub database and sub table < 3 >
Slf4j log facade
Redis 笔记 01:入门篇
1-2 project technology selection and structure
PHP導出word方法(一mht)
Shell: basic learning
2.8 overview of ViewModel knowledge
Integer int compare size
The future of cloud computing cloud native
DEJA_VU3D - Cesium功能集 之 054-模拟火箭发射全过程
If you can't learn, you have to learn. Jetpack compose writes an im app (II)
Use bloc to build a page instance of shutter
Is it OK to open an account for online stock speculation? Is the fund safe?
Official website of Unicode query
Shutter: add gradient stroke to font
4000字超详解指针
2.7 overview of livedata knowledge points
Dart: view the dill compiled code file
Self made pop-up input box, input text, and click to complete the event.