Gaussian distribution, linear regression, logistic regression

Gaussian distribution Gaussian distribution/ Normal distribution Normal distribution

1. Widespread presence

2020 year 11 month 24 Japan , The Chang'e 5 probe of the lunar exploration project was successfully launched . Its orbit is very important , According to Kepler's three laws, a curve can be calculated , But the curve is just an ideal orbit , The orbit in reality has errors , How to solve it ？ This problem has puzzled the scientific community for many years , Until Gauss published 《 The theory of celestial motion 》 There are specific solutions . The book introduces a method ： Least square method , The premise is that the measurement error should conform to the normal distribution .

“ Grosvenor LTD handsome ”, The height of an adult male in a country conforms to the Gaussian distribution ;“ double 11”, The sales volume of products also conforms to Gaussian distribution ;“CET-4/6”, Students' test scores also conform to Gaussian distribution ;“ Epidemic isolation 14 God ”,14 The sky is calculated from the Gaussian distribution …… There is a Gaussian distribution behind so many different events .

Shanghai randomly selected 1000 Men , Record everyone's height , Divide the data into 50 Intervals , Draw frequency histogram , Discover height 174cm The largest number of people , The left and right ends are very short / Tall people are few . Expand the data 10 times /100 times /10000 times , Draw the interval finer . A smooth curve can be drawn —— Gaussian distribution / Normal distribution .

2. Gaussian distribution

Normal distribution / Gaussian distribution curve Like a mountain peak , The height is steep and gentle ,（ Middle high , On both sides of the low , Symmetrical on both sides ）. It's determined by two parameters ： mean value μ（ Represents the average level of data ）、 Standard deviation σ（ Represents the degree of dispersion of data , The greater the standard deviation , Some values are far from the average , The more discrete , The slower the mountain grows ; The smaller the standard deviation , The value is close to the average , More agglomeration , The steeper the mountain .）

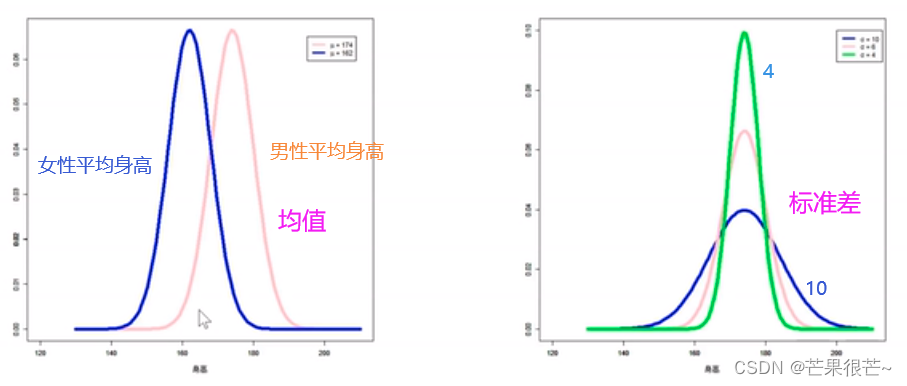
example ： Dove chocolate VS Apple , Dove package shows 43g, But there is a slight error with the actual situation , Its weight meets the average value of 43g Gaussian distribution of , The standard deviation is very small . Weigh each apple , Its weight also satisfies Gauss distribution , Assume that the average weight is 250g, So Apple's The actual weight revolves around the mean 250g Left right symmetrical distribution , Compared with virtue and blessing , Its standard deviation is very large .

3.3σ- Rules

 

 (μ-σ,μ+σ) Section , The probability of an event falling into it is 68.2%;（μ-2σ,μ+2σ）, The probability of the event falling is 95.4%;（μ-3σ,μ+3σ）, The probability of the event falling is 99.73%; Some people think  3σ- The rules are not strict enough , There are six Sigma Manage quality standards , That is, to expand the range to （μ-6σ,μ+6σ）, The probability of falling is 99.9998%, The probability of falling outside the range is only two in a billion .

4. Galton's nailboard experiment — “ The nine chapter ” The advent of quantum computers

 

 “ The nine chapter ” A new breakthrough in quantum computing in China , Solving mathematical algorithm Gaussian boson sampling The speed of just 200 second , And today's supercomputers use 6 In one hundred million, .

The Bose sampling device is not only the left or right choice of Galton's nailboard experiment , It interacts , And more than one photon at a time , It may be that a large number of photons are put together , This can lead to time-consuming problems .

Linear regression — Least square method

Draw the average daily traffic of coffee shops in the shopping mall （ The independent variables x） And average daily income ( The predicted variables , Dependent variable y) Scatter plot of the data .

Linear regression ： use A straight line To fit the relationship between independent variables and dependent variables （ linear equation y=kx+b）

How to get this line ？—— Least square method . Linear regression yields estimates , The closer the estimated value is to the actual value, the better , Represents the more accurate the estimated value .

Logical regression logistics regression = Linear regression +sigmoid function

An algorithm in data mining , What's the use ？ Used to solve binary classification problems . Don't be regressed by logic “ Return to ” Two words deceive ！！！

Classification problem ： Determine the category of data . Dichotomous problem ： There are only two types of target classes for classification problems

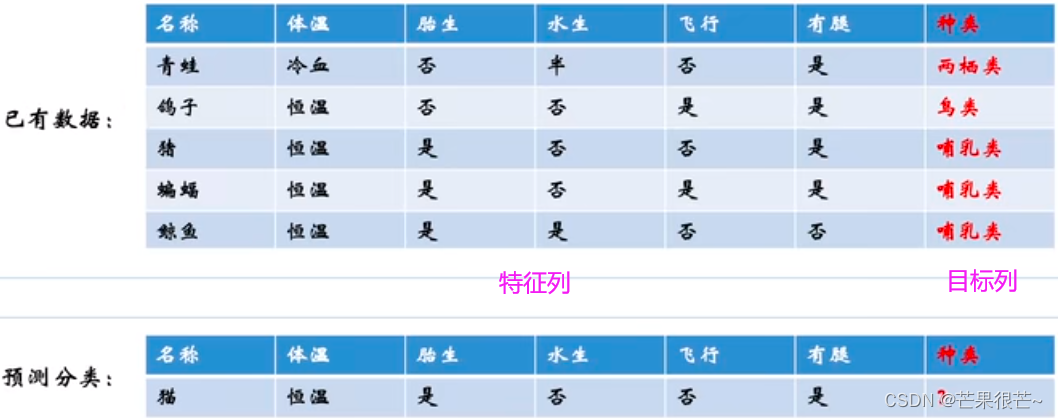
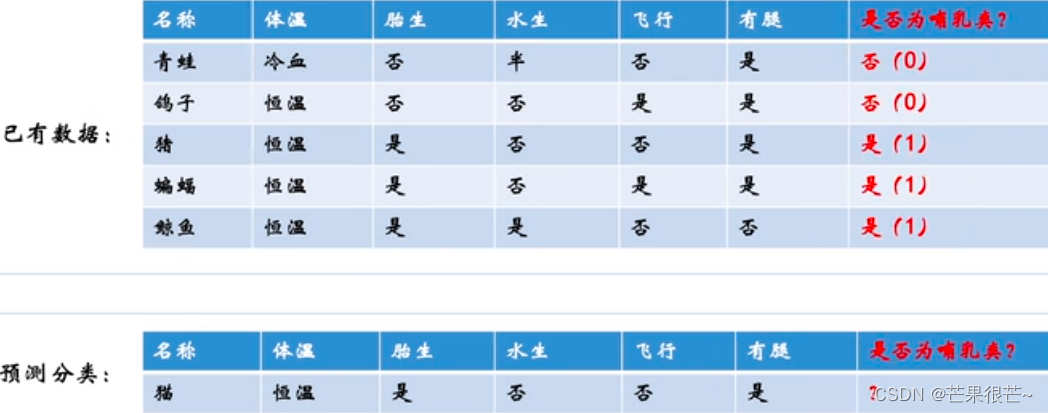
  The difference between regression and classification ？ The output of the regression model is continuous , The output of the classification model is discrete .

  Take the function value of linear regression as sigmoid Input to function

 

  How to solve

The smaller the loss function , The better the regression model ！ 

  There is no need to calculate by hand , The code can handle ！ You can use spark frame