The perceptron perceptron of Li Hang's "Statistical Learning Methods" notes

感知机(perceptron)

2.1 介绍

感知机(perceptron)是二类分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别,取+1和-1二值.Perceptron corresponds to输入空间(特征空间)中将实例划分为正负两类的分离超平面,属于判别模型.感知机学习旨在求出将训练数据进行线性划分的分离超平面,为此,导入Based on the misclassification of loss function,利用梯度下降法对损失函数进行极小化,求得感知机模型.感知机学习算法具有简单而易于实现的优点,分为原始形式和对偶形式.感知机预测是用学习得到的感知机模型对新的输入实例进行分类.感知机1957年由Rosenblatt提出,是神经网络与支持向量机的基础.

Structure to introduce perceptron model,感知机的学习策略,特别是损失函数,Perceptron learning algorithm,包括原始形式和对偶形式,并证明算法的收敛性.

2.1.2总结summarization

1.A straight line irrespective of the wrong one point,This is a good line.
2.Model as far as possible to find a good line.
3.If there is no good line,In line with poor find good line.
4.Judge straight how bad the way:Wrong point to a straight line distance sum,The greater the distance the model the worse.

2.2 定义

(感知机) 假设输入空间（特征空间) 是 $\mathcal{X} \subseteq \mathbf{R}^{n} $, 输出空间是 $ \mathcal{Y}={+1,-1}$ .输入 $ x \in \mathcal{X}$ 表示实例的特征向量, 对应于输入空间（特征空间）的点; 输出 $ y \in \mathcal{Y} $ 表示实例的类别.由输入空间到输出空间的如下函数:

KaTeX parse error: {align} can be used only in display mode.

称为感知机.其中, w 和 b 为感知机模型参数, $w\in {\mathbf{R}}^n$ 叫作权值 ( weight) 或权值向量 (weight vector), $b \in \mathbf{R} $ 叫作偏置 ( bias), $ w \cdot x $表示 w 和 x 的内积. $\operatorname{sign} $是符号函数, 即

KaTeX parse error: {align} can be used only in display mode.

感知机是一种线性分类模型, 属于判别模型.Perceptron model assumes that space is defined in All the model of linear classification in the feature space（linear classification model）或线性分类器（linear classifier）, 即函数集合$ {f \mid f(x)=w \cdot x+b} $.

感知机有如下几何解释: 线性方程

$w\cdot x+b=0$

2.3 参数说明

对应于特征空间 ${\mathbf{R}}^n$ 中的一个超平面 S , 其中w 是超平面的法向量, b 是超平面的截距.这个超平面将特征空间划分为两个部分.位于两部分的点 (特征向量) 分别被分为正、负两类.

Feature space is then维空间,Samples of each attribute is called a feature,Feature space mean all samples can be found in this space attribute combination.

因此, 超平面 S 称为分离超平面 (separating hyperplane), 如下图所示.

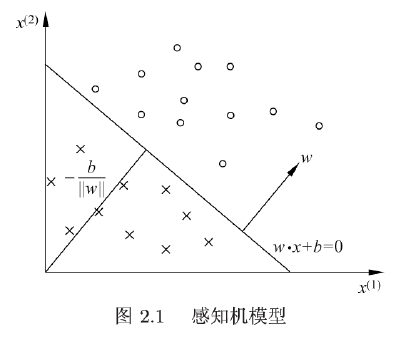
感知机学习, 由训练数据集 (实例的特征向量及类别)

$T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right)\right\}$

其中, $ x_{i} \in \mathcal{X}=\mathbf{R}^{n}, y_{i} \in \mathcal{Y}={+1,-1}, i=1,2, \cdots, N $, 求得感知机模型, 即求得模型参数 w, b .感知机预测, 通过学习得到的感知机模型, 对于新的输入实例给出其对应的输出类别.

2.4 Separable and not score according to the set

Compared with linear separable datasets and linear inseparable：

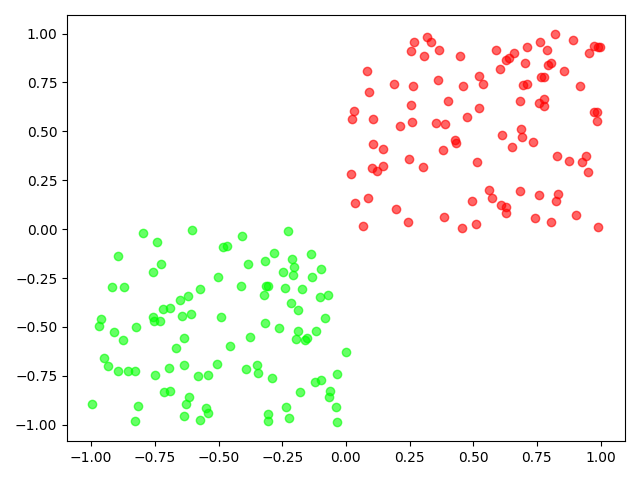
严格定义：

定义 2.2 (数据集的线性可分性) 给定一个数据集

$T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right)\right\}$

其中, $ x_{i} \in \mathcal{X}=\mathbf{R}^{n}, y_{i} \in \mathcal{Y}={+1,-1}, i=1,2, \cdots, N $, 如果存在某个超平面 S

$w\cdot x+b=0$

能将数据集的正实例点和负实例点完全正确地划分到超平面的两侧, 即对所有 $ y_{i}=+1$ 的实例 i , 有 $w \cdot x_{i}+b>0 $, 对所有 $ y_{i}=-1 $ 的实例 i , 有 $ w \cdot x_{i}+b<0 $, 则称数据集 T 为线性可分数据集 (linearly separable data set),否则,称数据集 T 线性不可分.

2.5 感知机的学习策略（Learning policy）

函数间隔与几何间隔
An arbitrary point in space $x_{0} $ 到超平面$ \mathrm{S}$ 的距离：

2.5.1 Function space

$\left|w\cdot x_0+b\right|$

Function space is not often use,Because such as proportion of larger or smallerw和bUnder the condition of invariable will make hyperplane can adjust the distance,Is not good to compare.

2.5.2 The geometric distance between

$\frac{1}{\Vert w\Vert }\left|w\cdot x_0+b\right|$ 其中$\Vert w{\Vert }_2$为$w$的$L_2范数$$ \quad|w|{2}=\sqrt{\sum{i=1}^{N} w_{i}^{2}}$

In geometric spacing is a good way to solve this problem：Proportion to such as enlarge shrinksw和b,通过L2Norm can offset to change.Therefore common geometric spacing.

2.5.3 感知机的学习算法——原始形式

For classification data by mistake,

$-y_i\left(w\cdot x_i+b\right)>0$

误分类点 $ x_{i} $ 到超平面 $\mathrm{S} $ 的距离为：(The absolute value can be removed)

$-\frac{1}{\Vert w\Vert }{y}_i\left(w\cdot x_i+b\right)$

因此,All the misclassification point（集合M）到超平面 S 的总距离为：

$-\frac{1}{\Vert w\Vert }{\sum }_{x_i\in M}{y}_i\left(w\cdot x_i+b\right)$

损失函数

$L(w,b)=-{\sum }_{x_i\in M}{y}_i\left(w\cdot x_i+b\right)$

2.5.4 Original form algorithm process

1.Selection of hyperplane $ w_{0}, b_{0}$ (做一个初始化)

2.Using the gradient descent method to minimize the objective function

$\begin{array}{l}L(w,b)=-{\sum }_{x_i\in M}{y}_i\left(w\cdot x_i+b\right)\\ {\nabla }_{w}L(w,b)=-{\sum }_{x_i\in M}{y}_i{x}_i\\ {\nabla }_{b}L(w,b)=-{\sum }_{x_i\in M}{y}_i\end{array}$

Adopted the interval function here,Because perception machine is误分类驱动,The ultimate goal is not a wrong sample（线性可分数据集）,So the final ideal for0,Then zoom parameters do not affect.Of course also can use geometric spacing.

3.更新 w, b

由$x_2=x_1-f^{\prime }(x_1)\eta$,可知

$\begin{array}{l}w\leftarrow w+\eta y_i{x}_i\\ b\leftarrow b+\eta y_i\end{array}$

注意,The above is for single point update,Each point is updated on a step.If in the following form,Is updated on a sample of all misclassification.

$\begin{array}{l}w\leftarrow w+{\sum }_{x_i\in M}{y}_i{x}_i\\ b\leftarrow b+{\sum }_{x_i\in M}{y}_i\end{array}$

2.5.5 例题

例 2.1 As shown in the training data set, It is instance point is $ x_{1}=(3,3)^{\mathrm{T}}, x_{2}=(4,3)^{\mathrm{T}} $, 负实例点是 $ x_{3}=(1,1)^{\mathrm{T}}$ , 试用感知机学习算法的原始形式求感知机模型 $f(x)= \operatorname{sign}(w \cdot x+b) $ .这里, $w=\left(w^{(1)}, w^{(2)}\right){\mathrm{T}}, x=\left(x^{(1)}, x^{(2)}\right){\mathrm{T}} $.

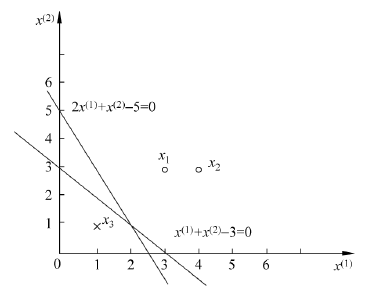
1.构建损失函数

$\min L(w,b)=-{\sum }_{x_i\in M}{y}_i\left(w\cdot x_i+b\right)$

2.梯度下降求解 w, b .设步长为 1

• 取初值 $w_{0}=0, b_{0}=0 $

• 对于 $ x_{1}, y_{1}\left(w_{0} \cdot x_{1}+b_{0}\right)=0$ Be classified correctly at the end of the,更新 w, b .

  $w_1=w_0+x_1{y}_1=(3,3{)}^T,b_1=b_0+y_1=1*w_1\cdot x+b_1=3x^{(1)}+3x^{(2)}+1$

3. 对 $x_{1}, x_{2} $ ,显然 $y_{i}\left(w_{1} \cdot x_{i}+b_{1}\right)>0 $ ,被正确分类,不作修改.对于 $ x_{3}, y_{3}\left(w_{1}\right. . \left.x_{3}+b_{1}\right)<0 $,被误分类,更新$ w , b$.

   $w_2=w_1+x_3{y}_3=(2,2{)}^T,b_2=b_1+y_3=0*w_2\cdot x+b_2=2x^{(1)}+2x^{(2)}$

4. 以此往复,直到没有误分类点,Minimal loss function to achieve.

This is taken successively in computing misclassification point $ x_{1}, x_{3}, x_{3}, x_{3}, x_{1}, x_{3}, x_{3} $ The separating hyperplane and perception machine model.If misclassification in calculation points in turn $x_{1}, x_{3}, x_{3}, x_{3}, x_{2}, x_{3}, x_{3}, x_{3}, x_{1}, x_{3}, x_{3} $ So the separation hyperplane is $ 2 x^{(1)}+x{(2)}-5=0 $ .
感知机学习算法由于Using different initial value or select different misclassification points, 解可以不同.