当前位置:网站首页>1. Finite Markov Decision Process
1. Finite Markov Decision Process
2022-07-03 10:09:00 【Most appropriate commitment】
Catalog
Finite Markov Decision Process
RL an introduction link:
Sutton & Barto Book: Reinforcement Learning: AnIntroduction
Finite Markov Decision Process
Definition
The ego (agent) monitors the situations from the environment, such as by data flow or sensors (cameras, lidars or others), which is called state in the view of term. We have to highlight that we presume the agent clearly know enough information of the situations all the time, by which the agent could make their decisions. So we have  at the time step of t.
at the time step of t.
After the agent knows the current state, it could have finite actions to choose (  ). And after taking an action, the agent will obtain the reward in this step (
). And after taking an action, the agent will obtain the reward in this step (  ) and run into the next state (
) and run into the next state (  ), in which process, the agent could know the environment's dynamics (
), in which process, the agent could know the environment's dynamics (  ).Then the agent will continue deal with this state until this scenario ends.
).Then the agent will continue deal with this state until this scenario ends.
The environment's dynamics are not decided by people, but the policy of taking which action depends on the agent's jugement. In every state  ,we could choose actions, which gives us more rewards totally not just in the short run, but also in the long run. Therefore, the policy of choosing actions in state is the core of reinforcement learning. we use
,we could choose actions, which gives us more rewards totally not just in the short run, but also in the long run. Therefore, the policy of choosing actions in state is the core of reinforcement learning. we use  to describe the probability of each action taken in the current state.
to describe the probability of each action taken in the current state.
Therefore, the Finite Markov Decision Process is the process,in which the agent know the current state ,actions that is about to choose, even the probability of  and
and  for each action (
for each action (  ) and obtain the expected return in different policy.
) and obtain the expected return in different policy.

Formula( Bellman equation )
Mathematically, we could calculate the value function  .
.
![v_{\pi } (s) = E[ G_t | S_t=s] = E[ R_{t+1} + \gamma G_{t+1} | S_t=s] = \sum_{a}^{}\pi (a|s)\sum_{s^{'}}^{}\sum_{r}^{}r p(r,s^{'} | a, s) [ r+ \gamma v_\pi ( s^{'} ) ]](http://img.inotgo.com/imagesLocal/202202/15/202202150539010556_1.gif)
Consideration
For every scenario, we know the dynamics of the environment  , the state set
, the state set  and coresponding action set
and coresponding action set  . For evey policy we set, we know
. For evey policy we set, we know  . So we could obtain N equations for
. So we could obtain N equations for  .
.
Limitation
- Many times, we could not know the dynamics of the environment.
- Many times, such as gammon, there are too many states. So we have no capacity to compute this probelm in this way ( solve equations )
- problems have Markov property, which means
 and
and  only depend on r and a. In other words, r and a could get all possible
only depend on r and a. In other words, r and a could get all possible  and
and  .
.
Optimal policies
Definition
For policy  and policy
and policy  , if for each state s, the ineuqation can be fulfilled:
, if for each state s, the ineuqation can be fulfilled:

then we can say  is better than
is better than  .
.
Therefore, there must be more than one policy, that is the optimal policy  .
.
At the meantime, every state in policy  also will meet Bellman equation.
also will meet Bellman equation.
![v_{\pi_{*} } (s) = \sum_{a}^{}\pi_{*} (a|s)\sum_{s^{'}}^{}\sum_{r}^{}r p(r,s^{'} | a, s) [ r+ \gamma v_{ \pi_{*} } ( s^{'} ) ]](http://img.inotgo.com/imagesLocal/202202/15/202202150539010556_12.gif)
Optimal Bellman equation
for  in the total policy set:
in the total policy set:
![v_{ \pi_{*}}(s)= max.\sum_{a} \pi(s|a)q(s,a) =max. \sum_{a}^{}\pi (a|s)\sum_{s^{'}}^{}\sum_{r}^{}r p(r,s^{'} | a, s) [ r+ \gamma v_{ \pi } ( s^{'} ) ]](http://img.inotgo.com/imagesLocal/202202/15/202202150539010556_11.gif)
For a specific case, the environment's dynamic is constant. We can only change the apportionment of  .
.
For a maximum v(s), we should apportion 1 to the max q(s,a).
Therefore, the optimal policy is actually a greedy policy without any exploration.
边栏推荐
- Application of external interrupts
- Notes on C language learning of migrant workers majoring in electronic information engineering
- Connect Alibaba cloud servers in the form of key pairs
- Mobile phones are a kind of MCU, but the hardware it uses is not 51 chip
- Retinaface: single stage dense face localization in the wild
- MySQL root user needs sudo login
- ADS simulation design of class AB RF power amplifier
- Synchronization control between tasks
- (2) New methods in the interface
- Of course, the most widely used 8-bit single chip microcomputer is also the single chip microcomputer that beginners are most easy to learn
猜你喜欢

2.Elment Ui 日期选择器 格式化问题

Assignment to '*' form incompatible pointer type 'linkstack' {aka '*'} problem solving

Cases of OpenCV image enhancement
Leetcode bit operation

Swing transformer details-2
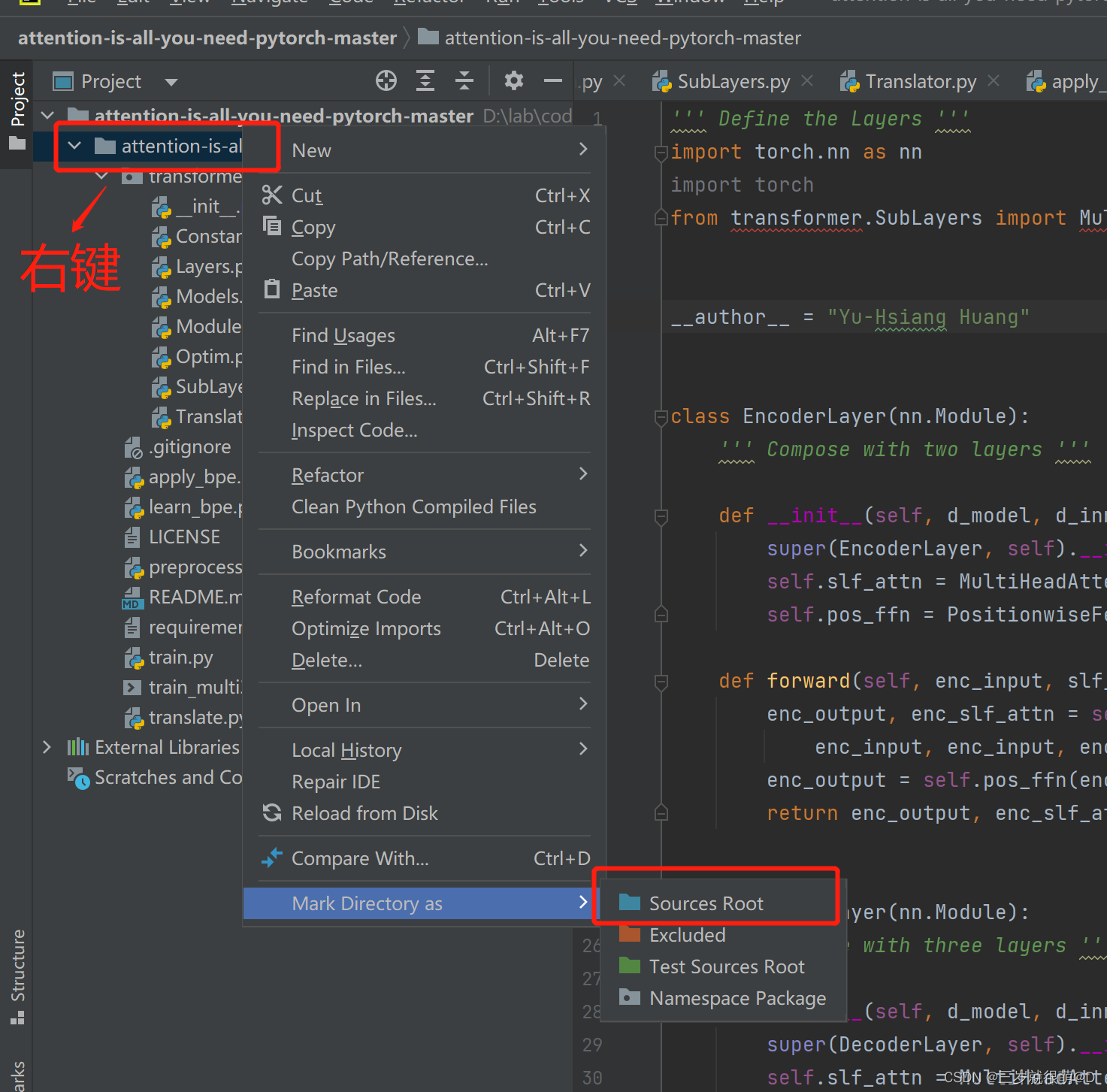
Pycharm cannot import custom package
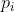
Retinaface: single stage dense face localization in the wild

Of course, the most widely used 8-bit single chip microcomputer is also the single chip microcomputer that beginners are most easy to learn

Opencv note 21 frequency domain filtering
Notes on C language learning of migrant workers majoring in electronic information engineering
随机推荐
It is difficult to quantify the extent to which a single-chip computer can find a job
LeetCode - 673. Number of longest increasing subsequences
Mobile phones are a kind of MCU, but the hardware it uses is not 51 chip
CV learning notes - camera model (Euclidean transformation and affine transformation)
RESNET code details
Opencv feature extraction sift
Cases of OpenCV image enhancement
Opencv Harris corner detection
Simulate mouse click
Gpiof6, 7, 8 configuration
自動裝箱與拆箱了解嗎?原理是什麼?
QT is a method of batch modifying the style of a certain type of control after naming the control
yocto 技术分享第四期:自定义增加软件包支持
2020-08-23
LeetCode - 706 设计哈希映射(设计) *
Opencv feature extraction - hog
getopt_ Typical use of long function
Leetcode - 1670 conception de la file d'attente avant, moyenne et arrière (conception - deux files d'attente à double extrémité)
The 4G module designed by the charging pile obtains NTP time through mqtt based on 4G network
(1) What is a lambda expression
 and
and  only depend on r and a. In other words, r and a could get all possible
only depend on r and a. In other words, r and a could get all possible