当前位置:网站首页>【[SCOI2005] 互不侵犯】【状压DP(含概念讲解)】
【[SCOI2005] 互不侵犯】【状压DP(含概念讲解)】
2022-08-02 15:28:00 【Eternity_GQM】
文章目录
什么是状压DP
状压 DP 是动态规划的一种,通过将状态压缩为整数来达到优化转移的目的。
如下图所示,可以用0/1表示状态,然后转换为十进制数进行存储,大大减少存储空间。
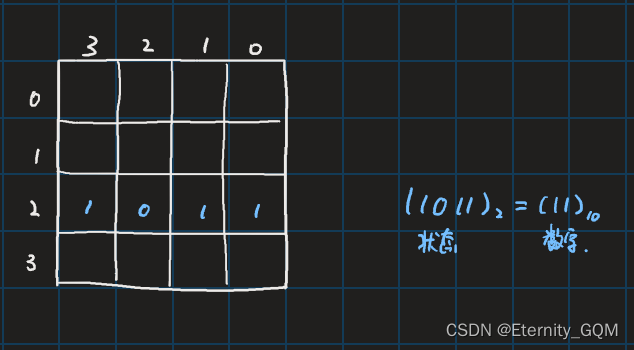
[SCOI2005] 互不侵犯
题目描述
在N×N的棋盘里面放K个国王,使他们互不攻击,共有多少种摆放方案。国王能攻击到它上下左右,以及左上左下右上右下八个方向上附近的各一个格子,共8个格子。
输入格式
只有一行,包含两个数N,K ( 1 <=N <=9, 0 <= K <= N * N)
输出格式
所得的方案数
样例 #1
样例输入 #1
3 2
样例输出 #1
16
思路分析
数组f[i][st][j]的定义,以及状态转移方程:

不合法检验:
行内不能相邻,行间要检验三位。
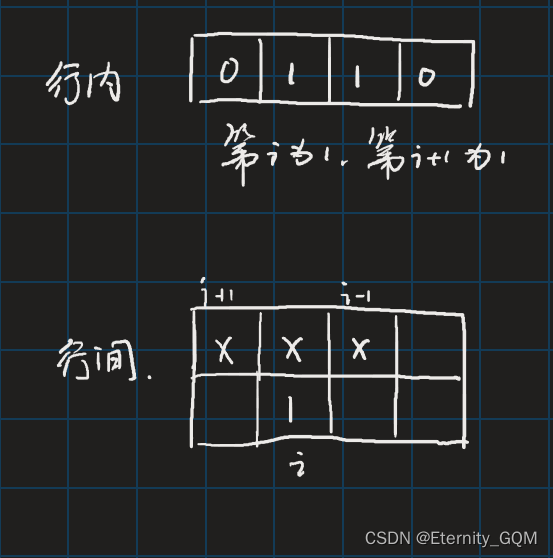
st 的范围(状态数组的大小):

代码
int n, k;
ll f[9][1 << 9][82], ans;
int c(int st){
//返回st的二进制中1的个数
int cnt = 0;
while(st){
if(st%2)
cnt++;
st /= 2;
}
return cnt;
}
bool check1(int st){
//同行检验
for (int i = 0; i < n - 1;i++)
if ((st & (1 << i)) && (st & (1 << (i + 1))))
return false;
return true;
}
bool check2(int st,int st2){
//与上一行的检验
for (int i = 0; i < n;i++){
if (st & (1 << i)){
if (st2 & (1 << i))
return false;
else if (i + 1 < n && (st2 & (1 << (i + 1))))
return false;
else if (i - 1 < n && (st2 & (1 << (i - 1))))
return false;
}
}
return true;
}
void solve(){
cin >> n >> k;
for (int i = 0; i < n;i++){
for (int st = 0; st < (1 << n);st++){
if(!check1(st))
continue;
if (i == 0)
f[i][st][c(st)] = 1;
else{
for (int j = c(st); j <= k;j++){
for (int st2 = 0; st2 < (1 << n);st2++){
if(!check1(st2)||!check2(st,st2))
continue;
f[i][st][j] += f[i - 1][st2][j - c(st)];
}
}
}
}
}
for (int st = 0; st < (1 << n);st++)
ans += f[n - 1][st][k];
cout << ans << nl;
}
边栏推荐
猜你喜欢
Thinkpad E430c使用u盘安装系统

UnicodeEncodeError: 'gbk' codec can't encode character '\u2022' in position 178: illegal multibyte s

MySQL【数据类型】

06-线程池(3大方法、7大参数,4种拒绝策略)
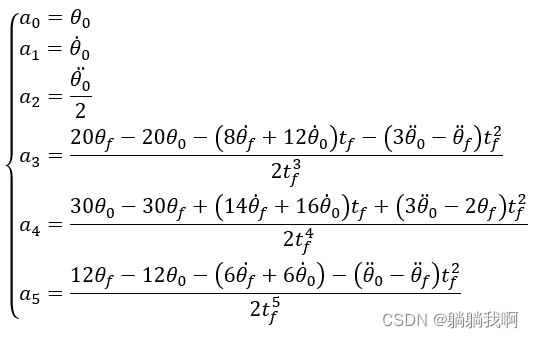
机械臂速成小指南(十四):多项式插值轨迹规划
先睹为快!界面控件DevExpress WPF这些功能即将发布

【服务器数据恢复】Raid阵列更换故障硬盘后数据同步失败的数据恢复案例
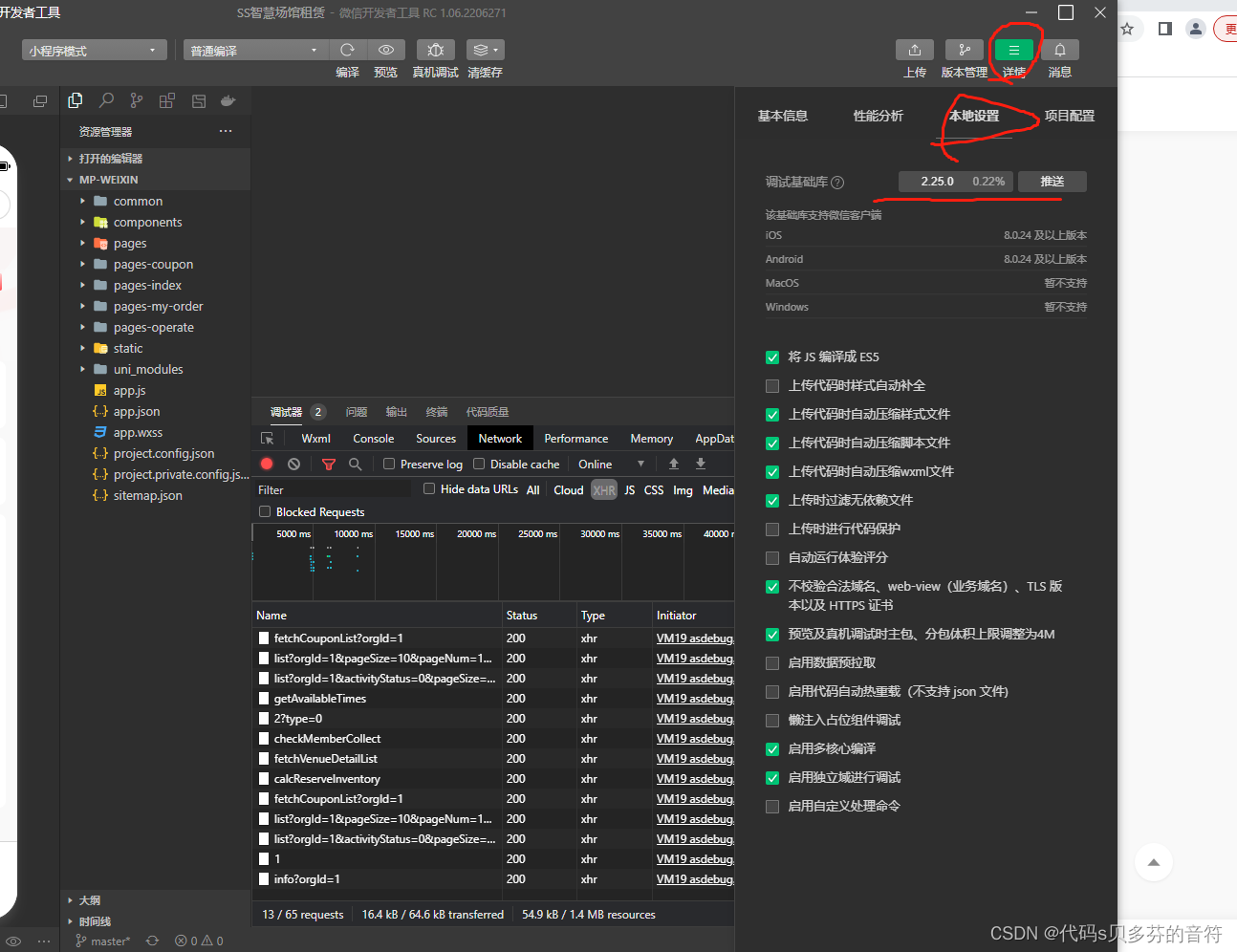
微信小程序:Framework inner error FLOW_CREATE_NODE

Basic management of system storage -- mounts, partitions, user quotas

太帅了!我用炫酷大屏展示爬虫数据!
随机推荐
太帅了!我用炫酷大屏展示爬虫数据!
【个人总结】2022.7月结
一文搞懂│php 中的 DI 依赖注入
word公式复制到另一个word当中出现图片解决方案
SIGIR'22 推荐系统论文之POI篇
机械臂速成小指南(十四):多项式插值轨迹规划
Eight big software attack overview of supply chain
先睹为快!界面控件DevExpress WPF这些功能即将发布
tiup mirror publish
助力疫情防控,30行代码就能搞定无服务器实时健康码识别!
轻松入门自然语言处理系列 专题8 源码解读──基于HMM的结巴分词
第十四天笔记
ROS 之 KUKA iiwa编程
SSRF(服务器端请求伪造)
剑指Offer 49.丑数 动态规划
如何利用PHP实现词法分析器与自定义语言
VLAN实验
面试官的角度谈谈算法岗面试的过程(岗位涉及到OCR、目标检测、图像分割、语音识别等领域)
为什么我不再推荐枚举策略模式?
做好私域流量!全民拼购就可以了。