当前位置:网站首页>A digit DP
A digit DP
2022-06-11 02:31:00 【Dongdongyu】
bernays , Learn a number in one night dp Not bad, hehe
As the title :
600. There is no continuity 1 Non-negative integer
Given a positive integer n , The return range is [0, n] All nonnegative integers , Its binary representation does not contain Successive 1 The number of .
Namely dp[i][j] Express i The number of digits is j start , How many kinds are there .
In this case dp[i][j]=dp[i-1][k]( Sum according to the right )
Then there may be a mess of rules in the title , For example, continuous 1, Discontinuous 1, Does not contain a certain number … wait ; At this time, just change dp Array can , But notice , Inside dp Just initialize .
If it is to ask for 0~n Number on interval , Now all we have is the number of digits , To do ?
Refer to the idea of tree arrays , For example 324 The number of , First seek dp[3][0]+dp[3][1]+dp[3][2]; In this way, less than 300 All of them have been worked out , And then ask dp[2][0]+dp[2][1], This way <320 All of them can be found out , It can be seen as holding down a number from the high position to keep it unchanged, and then changing the value of the low position . This problem is solved according to binary system , Then check whether the high position is continuous when required 1, If yes, this dp Value cannot be added
Post a code :
int dp[40][2];
int digit[40];
int check(int *p,int size)
{
for(int i=1;i<size;i++)
{
if(p[i]==1&&p[i-1]==1)
{
return 0;
}
}
return 1;
}
int findIntegers(int n)
{
for(int i=0;i<40;i++)
{
dp[i][0]=0;
dp[i][1]=0;
digit[i]=0;
}
dp[1][1]=1;
dp[1][0]=1;
for(int i=2;i<40;i++)
{
dp[i][0]=dp[i-1][0]+dp[i-1][1];
dp[i][1]=dp[i-1][0];
}
int end=39;
int start;
int flag=1;
for(start=end;n!=0;start--)
{
digit[start]=n%2;
n=n/2;
if(start<39&&digit[start+1]==1&&digit[start]==1)
flag=0;
}
start++;
int ans=0;
int len=end-start+1;
int init=start;
for(int i=start;i<=end;i++)
{
for(int j=0;j<digit[i];j++)
{
if(check(&digit[init],i-init))
ans+=dp[(end-i)+1][j];
// ans+=dp[(end-i)+1][1];
}
}
return ans+flag;
}
边栏推荐
- 如何保障数仓数据质量?
- 2022 simulated 100 questions and answers for crane driver (limited to bridge crane) examination
- [untitled]
- ADVANCE.AI首席执行官寿栋将在2022新兴市场品牌出海线上峰会分享跨境电商运用AI技术合规
- Unity3d model skin changing technology
- Byte beating client R & D Intern Tiktok side
- Jetpack Compose Scaffold和TopAppBar(顶部导航)
- 【AI周报】AI与冷冻电镜揭示「原子级」NPC结构;清华、商汤提出「SIM」方法兼顾语义对齐与空间分辨能力
- Nodejs send mail
- The largest kth element in the array
猜你喜欢

MOFs, metal organic framework materials of folic acid ligands, are loaded with small molecule drugs such as 5-fluorouracil, sidabelamine, taxol, doxorubicin, daunorubicin, ibuprofen, camptothecin, cur

Jetpack Compose Scaffold和BottomAppBar(底部导航)

多级介孔有机金属骨架材料ZIF-8负载乳酸氧化酶(LOD)/四氧化三铁(Fe304)/阿霉素DOX/胰岛素/cas9蛋白/甲硝唑/大黄素甲醚

421. maximum XOR value of two numbers in the array
Tencent test development post interview programming questions

如何保障数仓数据质量?

The most complete format description of clang format

421. 数组中两个数的最大异或值

Find - (half find / half find)
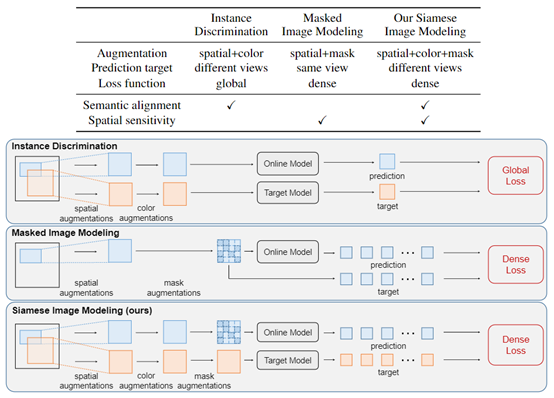
【AI周报】AI与冷冻电镜揭示「原子级」NPC结构;清华、商汤提出「SIM」方法兼顾语义对齐与空间分辨能力
随机推荐
Knowledge competition of safety production month -- how much do you know about new safety law
92. actual combat of completable future
GCC C内联汇编
aspects to consider for a recommendation letter
P4338 [ZJOI2018]历史(树剖)(暴力)
Unity determines whether the object is in the camera field of view
Sd3.0 notes
[untitled]
Why can some programmers get good offers with average ability?
About stepping on the pit diary and the association of knowledge points
查看Redis内数据,除了命令行和客户端,你还有第三种选择
SQL | 返回顾客名称和相关订单号以及每个订单的总价
The annual salary of testers in large factories ranges from 300000 to 8K a month. Roast complained that the salary was too low, but he was ridiculed by netizens?
Kotlin apply method
clang-format 最全格式说明
STC8A8K64D4 EEPROM读写失败
421. maximum XOR value of two numbers in the array
年金保险理财产品可以复利吗?利率是多少?
Epoll principle and Application & ET mode and lt mode
Introduction for i-Teams