当前位置:网站首页>递归思想
递归思想
2022-08-04 08:30:00 【小艾菜菜菜】
什么是递归
首先我觉得我们要清楚什么是递归
递归在于不断调用自己的函数,层层深入,直到遇到递归终止条件后层层回溯,其思想与dfs的思想不谋而合;因此,可以使用递归来实现dfs。
递归的进入比较容易理解,但是递归的回溯是在计算机底层执行的,我们无法看到。因此,递归究竟是如何完成的,成为了理解递归的一大难点,也是理解递归的唯一一个难点。
理解递归
让我们来看一下这样一个简单的递归程序:
#include<iostream>
using namespace std;
int n;
void func(int u){
if(u == 0) return;
cout << "Recursive program goes to the next level --- " << u << endl;
func(u-1);
cout << "Recursive program backtracking --- " << u <<endl;
return;
}
int main(){
cin >> n;
func(n);
return 0;
}
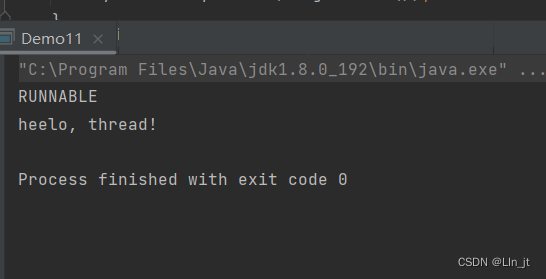
输入3,我们可以看到,它的输出是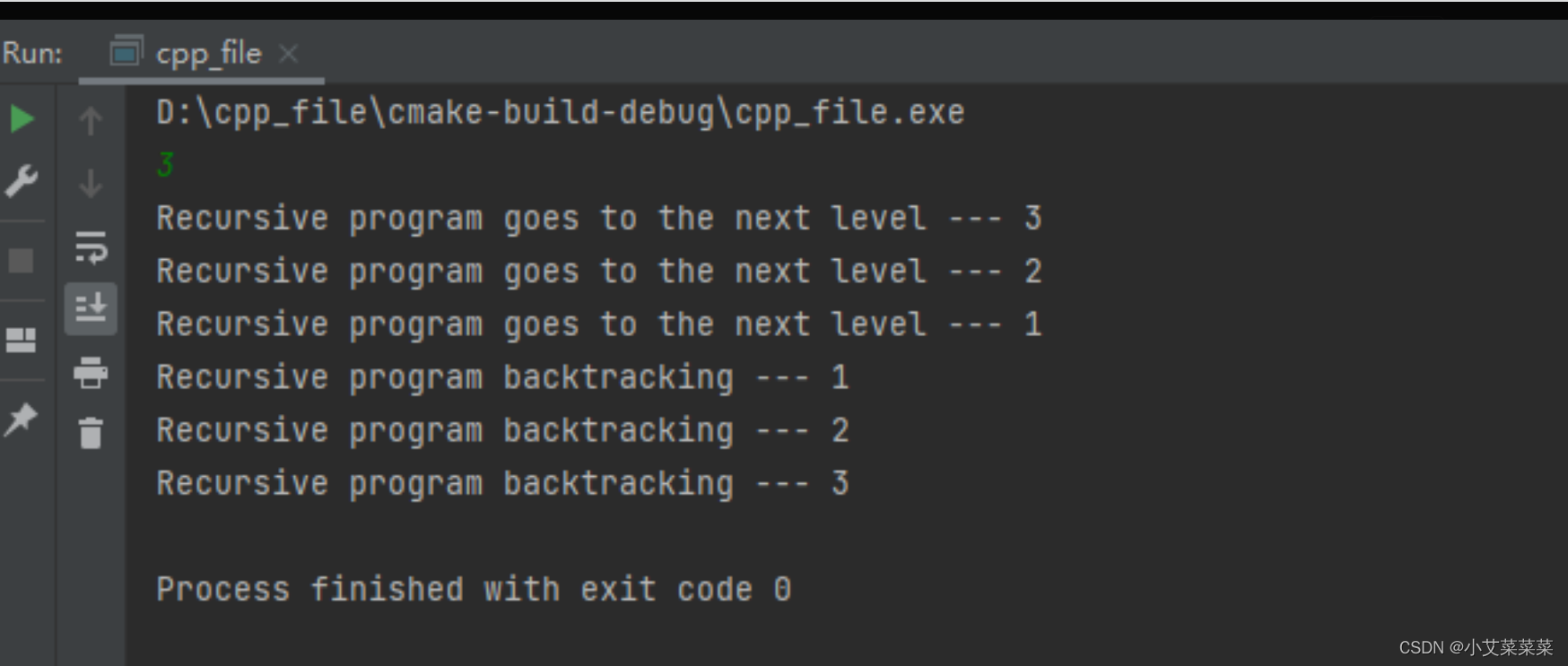
我们可以清楚的看到,哪个数字进入了递归,又有哪个数字回溯了。
为什么会产生这样的结果?请看下面这幅图,它解释了递归函数的调用全过程
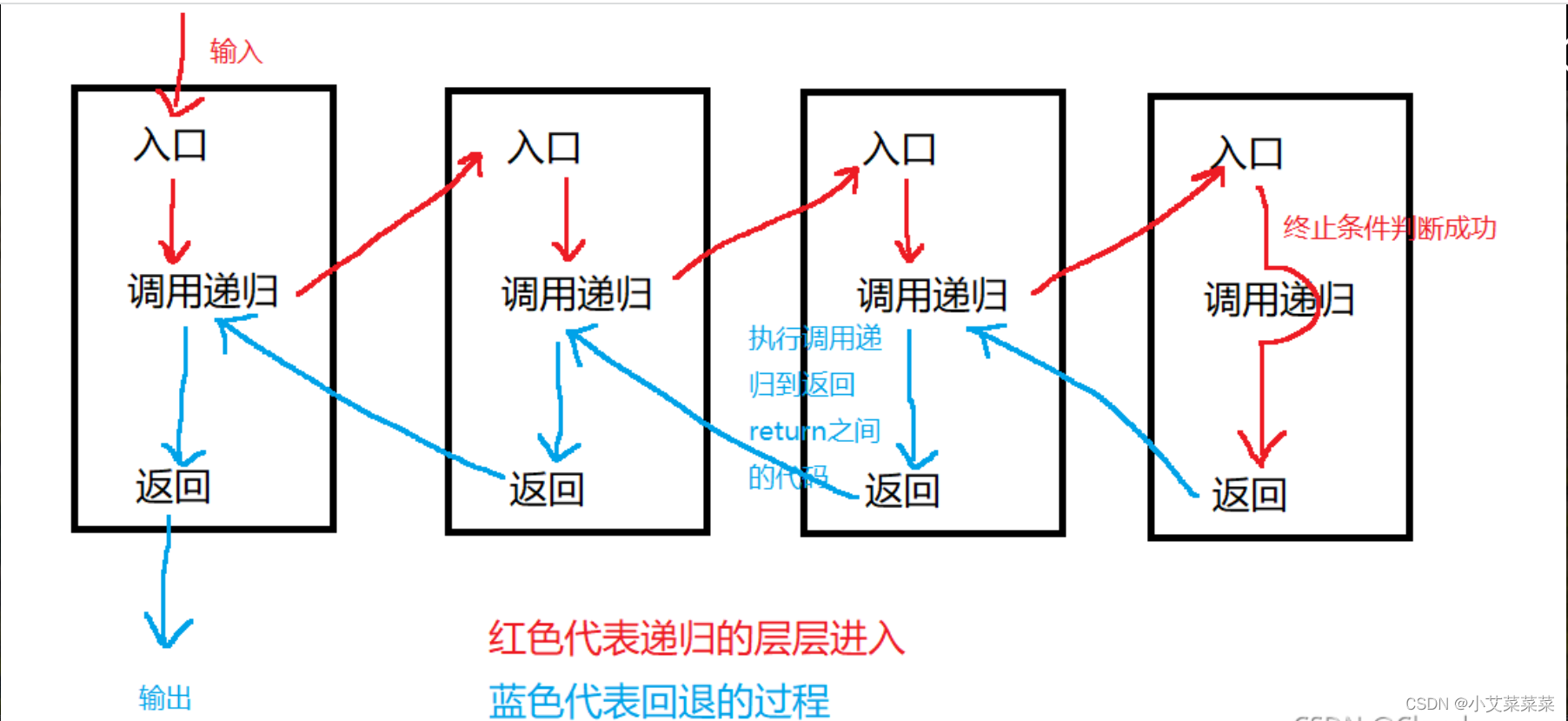
这样,我们就能理解,为什么首先输出的是Recursive program backtracking — 1了
如果还不是很理解,请看下面的图,我们从u = 0 回退到了u = 1,再直接回退到u = 2,再回退到u = 3
递归程序在回退完成前,return会使得计算机继续依次执行上一层函数调用后的代码。
再结合一道题来进一步理解递归思想的应用过程
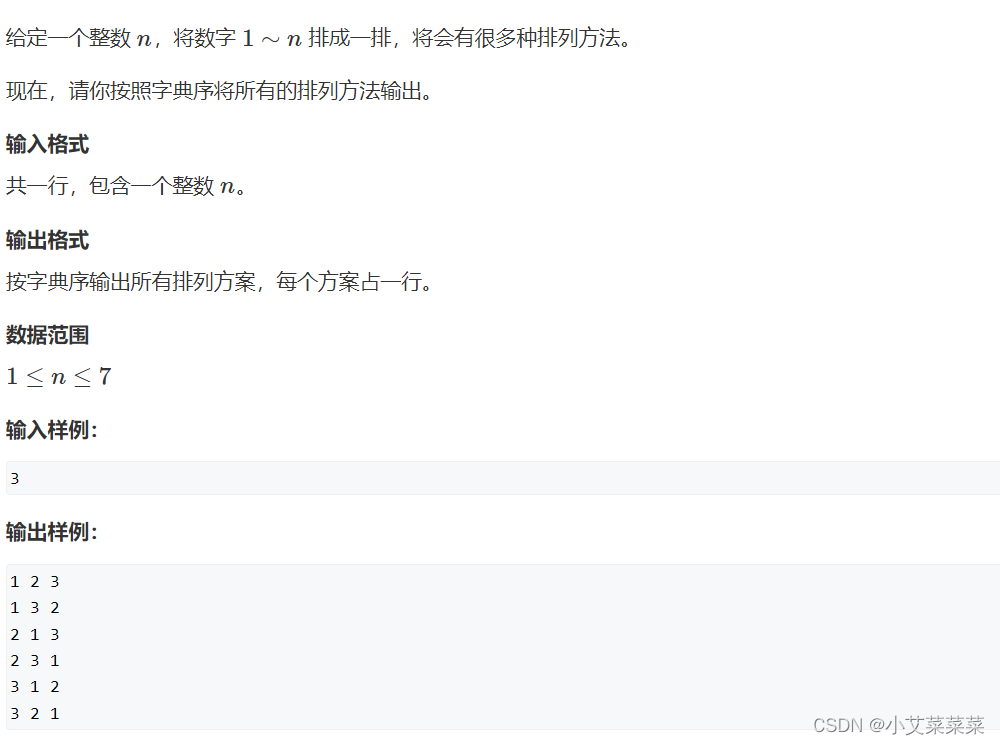
全排列
解题思路
如何用dfs 解决全排列问题?
注意: dfs 最重要的是搜索顺序。
对于全排列问题, 以 n = 3为例,可以这样进行搜索: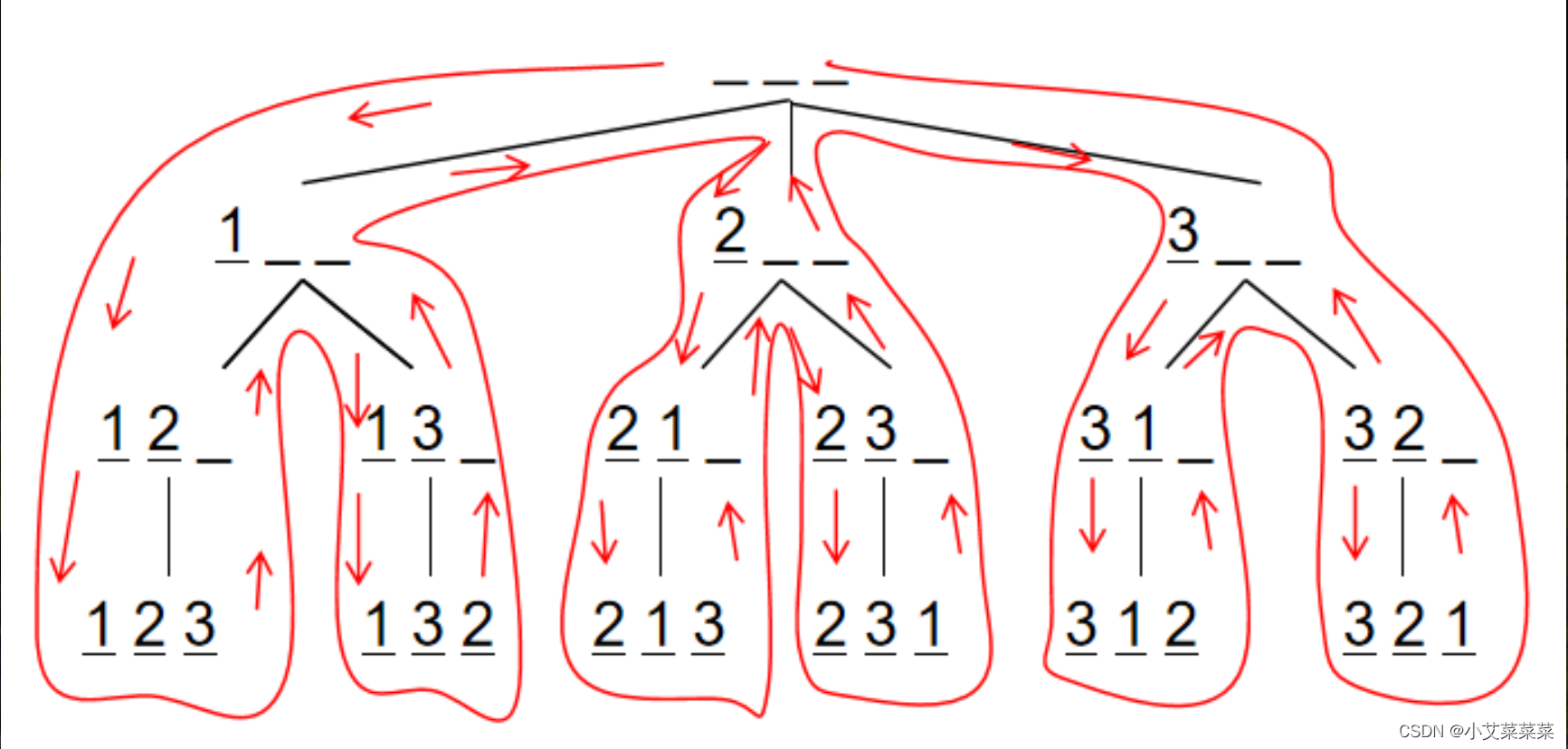
具体实现过程描述如下:
假设有三个空位,从前往后填数字,每次填一个位置,填的数字不能和前面的一样。
开始的时候,三个空位都是空的:__ __ __
首先填写第一个空位,第一个空位可以填 1,填写后为:1 __ __
填好第一个空位,填第二个空位,第二个空位可以填 2,填写后为:1 2 __
填好第二个空位,填第三个空位,第三个空位可以填 3,填写后为: 1 2 3
这时候,空位填完,无法继续填数,所以这是一种方案,输出。
然后往后退一步,退到了状态:1 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3 ,没有其他数字可以填。
因此再往后退一步,退到了状态:1 __ __。第二个空位上除了填过的 2,还可以填 3。第二个空位上填写 3,填写后为:1 3 __
填好第二个空位,填第三个空位,第三个空位可以填 2,填写后为: 1 3 2
这时候,空位填完,无法继续填数,所以这是一种方案,输出。
然后往后退一步,退到了状态:1 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2,没有其他数字可以填。
因此再往后退一步,退到了状态:1 __ __。第二个空位上除了填过的 2,3,没有其他数字可以填。
因此再往后退一步,退到了状态:__ __ __。第一个空位上除了填过的 1,还可以填 2。第一个空位上填写 2,填写后为:2 __ __
填好第一个空位,填第二个空位,第二个空位可以填 1,填写后为:2 1 __
填好第二个空位,填第三个空位,第三个空位可以填 3,填写后为:2 1 3
这时候,空位填完,无法继续填数,所以这是一种方案,输出。
剩下的以此类推哦~
代码实现
变量的说明:
用path 数组保存排列,当排列的长度为 n 时,是一种方案,输出。
用st 数组表示数字是否用过。当st[i]为true 时,i 已经被用过了,st[i] 为 false 时,i 没被用过。
dfs(i) 表示的含义是:在path[i] 处填写数字,然后递归的在下一个位置填写数字。
回溯:第 i 个位置填写某个数字的所有情况都遍历后, 第 i 个位置填写下一个数字。
#include<iostream>
using namespace std;
const int N = 10;
int n;
int path[N]; // 保存序列
bool st[N]; //判断数字是否用过
void dfs(int u)
{
if (n == u) //数字填完,输出
{
for (int i = 0; i < n; i++) printf("%d ",path[i]);
puts("");
return;
}
for (int i = 1; i <= n; i++)
{
if (!st[i])
{
path[u] = i; // 放入空位置
st[i] = true; // 数字备用修改状态
dfs(u + 1); // 填写下一个位置
path[u] = 0; // 回溯之前可以将空位置设置为0
st[i] = false; // 回溯取出i
}
}
}
int main()
{
cin >> n;
dfs(0);
return 0;
}
总结
个人觉着dfs模板题,推荐完全背下来。递归的思想也要好好的理解并掌握。
最后如果还是不太懂这递归的思想,推荐看这篇博客
边栏推荐
- 一天学会JDBC06:PrepaerdStatemtnt
- 一天搞定JDBC02:开启事务
- LeetCode每日五题01:两数之和 (均1200题)
- 金仓数据库 KDTS 迁移工具使用指南 (4. BS 版使用说明)
- C# 实用的第三方库
- [NOI Simulation Competition] Paper Tiger Game (Game Theory SG Function, Long Chain Division)
- 并查集介绍和基于并查集解决问题——LeetCode 952 按公因数计算最大组件大小
- 高等代数_证明_对称矩阵属于不同特征值的特征向量正交
- 金仓数据库 KDTS 迁移工具使用指南 (6. 注意事项)
- 力扣 剑指 Offer 04. 二维数组中的查找
猜你喜欢
随机推荐
leetcode 22.8.1 二进制加法
技术实现 | 图像检索及其在高德的应用
安装GBase 8c数据库集群时,报错误码:80000306,显示Dcs cluster not healthy。怎么处理错误呢?
经典二分法查找的进阶题目——LeetCode33 搜索旋转排序数组
Distributed Computing Experiment 4 Random Signal Analysis System
powershell和cmd对比
inject() can only be used inside setup() or functional components.
【论文笔记】Dynamic Convolution: Attention over Convolution Kernels
给Unity Behavior Designer(Unity行为树) 的Can See Object 画圆锥辅助图
微信消息从发送到接收,经历了什么?如何防止丢包
智能健身动作识别:PP-TinyPose打造AI虚拟健身教练!
大佬们,mysql里text类型的字段,FlinkCDC需要特殊处理吗 就像处理bigint uns
智汇华云 | 华云软件定义网络 DCI介绍
C# DirectoryInfo类
DWB主题事实及ST数据应用层构建,220803,,
<jsp:useBean>动作的使用
金仓数据库KingbaseES客户端编程接口指南-JDBC(8. JDBC 元数据处理)
华为设备配置VRRP与路由联动监视上行链路
【CNN基础】转置卷积学习笔记
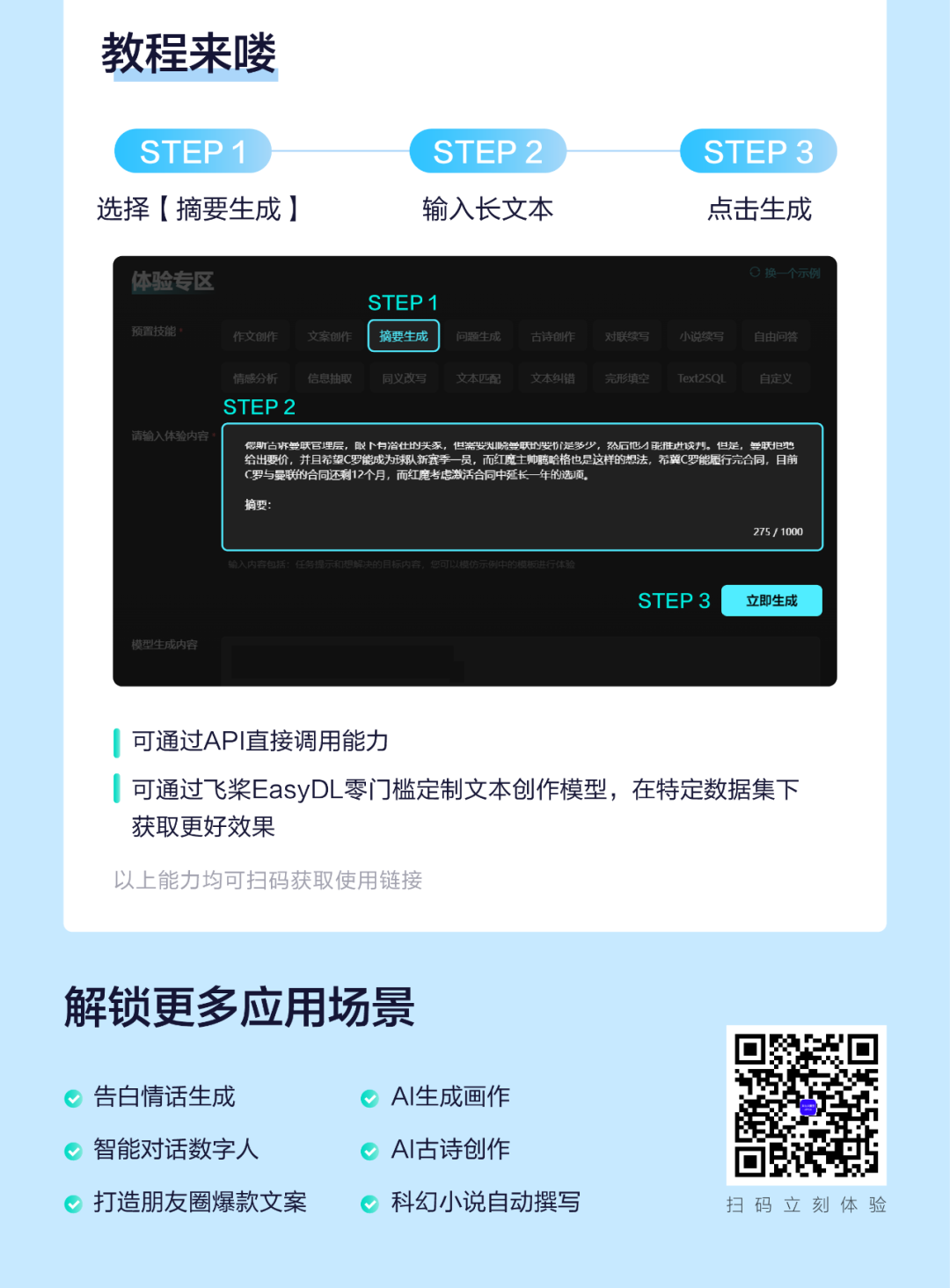
秒懂大模型 | 3步搞定AI写摘要