【点云处理之论文狂读前沿版12】—— Adaptive Graph Convolution for Point Cloud Analysis

摘要

• 问题： 标准的卷积操作无法在3D点间有区分地表示特征对应关系
• 方法： 本文提出Adaptive Graph Convolution(AdaptConv)，根据3D点动态学习的特征生成自适应的kernel
  1. 与使用固定/等向的kernel相比，AdaptConv提高了point cloud卷积的灵活性，有效并精确地得到不同语义部分点间的多种关系
  2. 与使用注意力权重的方法不同，AdaptConv使得卷积操作更加具有自适应性，而不是简单的为neighboring points分配不同的权重
• 代码：PyTorch版本

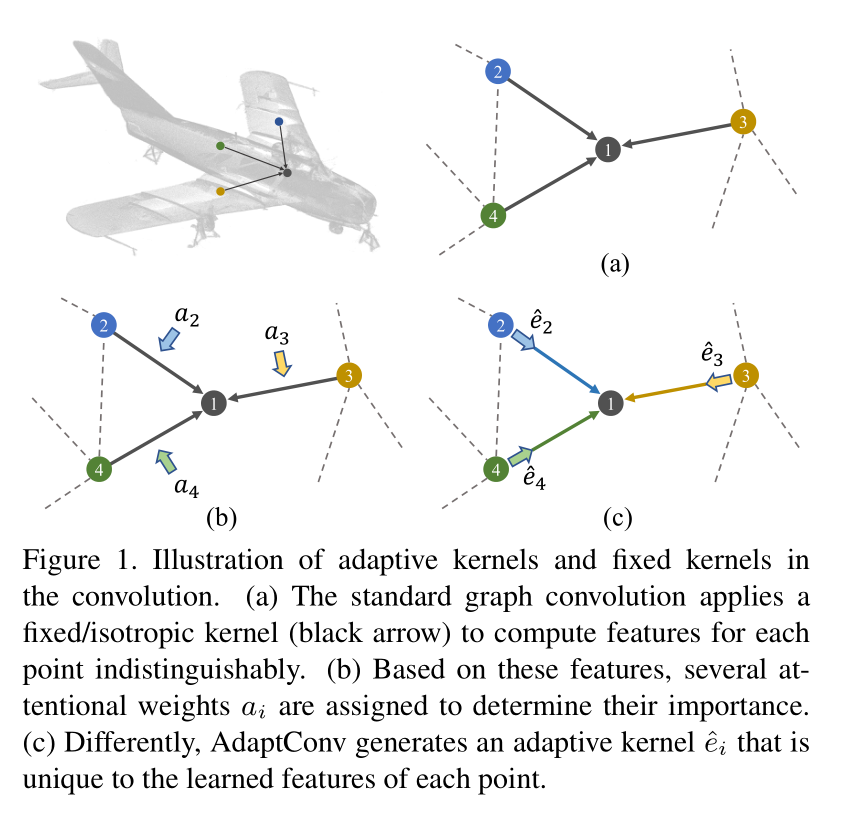
引言

Graph CNNs根据点间的空间/特征相似性将point cloud表示为graph数据，并将images上的2D卷积推广到3D点上。

标准的Graph CNNs通常会在每对点上使用共享权重函数抽取这对点的对应边特征，这会导致得到一个固定/同向的卷积kernel，当作用在所有点对上后，会忽略掉不同特征的对应关系。

该项工作的关键贡献在于AdaptConv能够在graph卷积内使用，而不是基于结果特征的权重函数。

此外，还开发了一些特征卷积设计，能够更加灵活地进行适应性卷积。

方法

Adaptive graph convolution

记$\mathcal{X}=\{x_i\mid i=$$1,2,\dots ,N\}\in {\mathbb{R}}^{N\times 3}$为输入点云，$\mathcal{F}=\left\{f_i\mid i=1,2,\dots ,N\right\}\in {\mathbb{R}}^{N\times D}$为对应的特征，其中$x_i$表示第第$i$个点的 $(\mathbf{x},\mathbf{y},\mathbf{z})$坐标，在其他情况下，还可以和其他特征进行结合。

然后根据给定的点云计算有向图 $\mathcal{G}(\mathcal{V},\mathcal{E})$，其中$\mathcal{V}=\{1,\dots ,N\}$和$\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ 表示顶点和边的集合。通过包含self-loop的$k$-nearest neighbors (KNN)构造graph。

在给定输入的$D$维特征后，AdaptConv layer会产生一组新的$M$维特征，点的数量和输入相同。与之前的graph convolution层相比，更能精确地反应局部结构特性。

记$x_i$是graph convolution的中心点，$\mathcal{N}(i)=\{j:(i,j)\in \mathcal{E}\}$是相邻点的索引。由于点云的不规则性，之前的方法通常会在$x_i$的所有neighbored points上应用固定的kernel函数，用于捕获patch的几何信息。但是，不同的neighbored points可能会得到对应$x_i$不同的特征，特别是当$x_i$位于显著区域，比如角或者边处。 在这种情况下，固定的kernel可能无法从graph convolution得到用于分类或分割的几何表示信息。

在本文的方法中，设计了一种自适应性kernel，用于计算每对点之间的显著关系。对于$M$维输出特征的每一个通道，AdaptConv会动态地生成一个kernel，使用的是应用在points特征$\left(f_i,f_j\right)$ 上的函数：
$${\hat{e}}_{ijm}=g_m\left(\Delta f_{ij}\right),j\in \mathcal{N}(i).$$
其中$m=1,2,\dots ,M$表示$M$个输出维度的一个，对应于一个单独的filter。$\Delta f_{ij}=\left[f_i,f_j-f_i\right]$用于捕获全局结构和局部领域特征，$[\cdot ,\cdot ]$是拼接操作，$g(\cdot )$是特征映射函数，即$MLP$。

与2D卷积中的计算一样，将$D$维输入和对应的filter权重进行卷积得到$M$维输出中的一维，本文将adaptive kernel和对应的点$\left(x_i,x_j\right)$进行卷积：
$$h_{ijm}=\sigma *{\hat{e}}_{ijm},\Delta x_{ij}*,$$
其中$\Delta x_{ij}$被定义为$\left[x_i,x_j-x_i\right]$相似性，$*\cdot ,\cdot *$表示两个向量的内积，输出为$h_{ijm}\in \mathbb{R}$，$\sigma$是非线性激活函数。

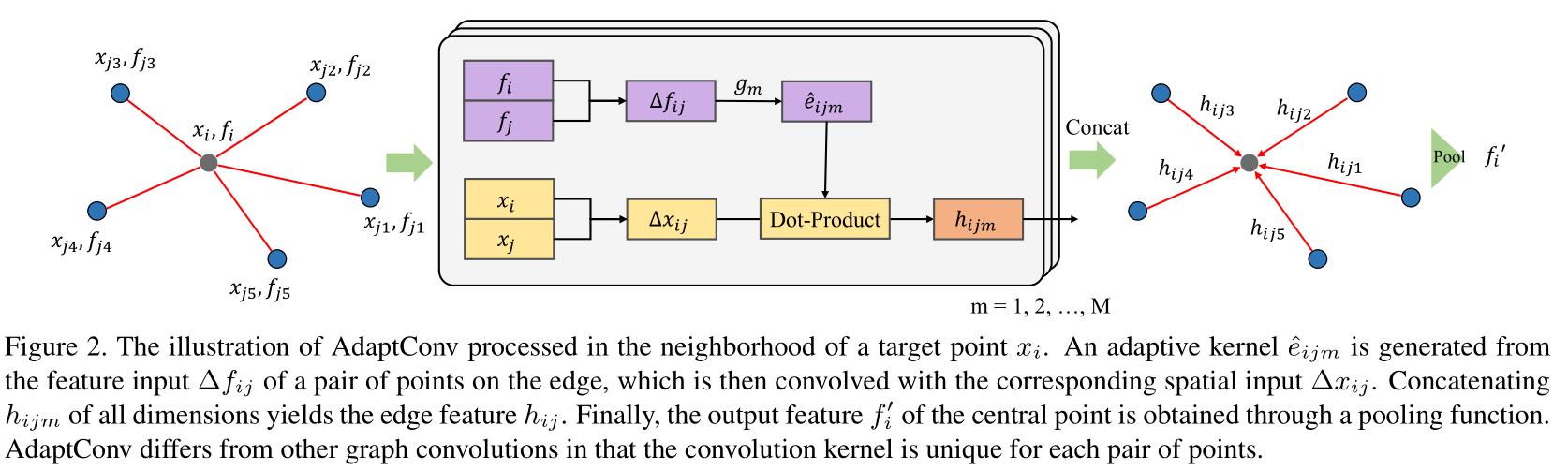
如图2所示，第$m$个adaptive kernel${\hat{e}}_{ijm}$与对应点$x_j\in {\mathbb{R}}^3$的spatial relations $\Delta x_{ij}$结合，表示kernel的大小应当与内积相匹配，即特征映射$g_m:{\mathbb{R}}^{2D}\to {\mathbb{R}}^6$。存储每个通道的$h_{ijm}$，得到连接点$\left(x_i,x_j\right)$间的边特征 $h_{ij}=$$\left[h_{ij1},h_{ij2},\dots ,h_{ijM}\right]\in {\mathbb{R}}^M$。

最后，通过利用邻域内所有边特征的聚合函数得到central point $x_i$的输出特征：
$$f_i^{\prime }=\underset{j\in \mathcal{N}(i)}{\max }{h}_{ij},$$
其中max是以通道为单位的max-pooling函数。总之，AdaptConv的convolution weights被定义为defined as $\Theta =\left(g_1,g_2,\dots ,g_M\right)$。

Feature decisions

就是利用特征去寻找空间关系。

如果输入$x_i\in {\mathbb{R}}^E$包含了更多的信息，那就是另外的选项，在实验中会考虑到。

将空间信息$\Delta x_{ij}$替换为特征信息 $\Delta f_{ij}$，会得到不同的${\hat{e}}_{ijm}$，这个也是可以考虑的选项。

本文选择使用$\Delta x_{ij}$作为变换域有着如下的考虑：

1. 点特征已经被用于生成adaptive kernel了，在使用特征进行卷积会导致特征信息的冗余
2. 特征的维度高，MLP在高维空间中学习起来很困难
3. 消耗内存大，计算复杂度高

Network architecture

graph的结构在每一层都是动态更新的

实验

Classifcation

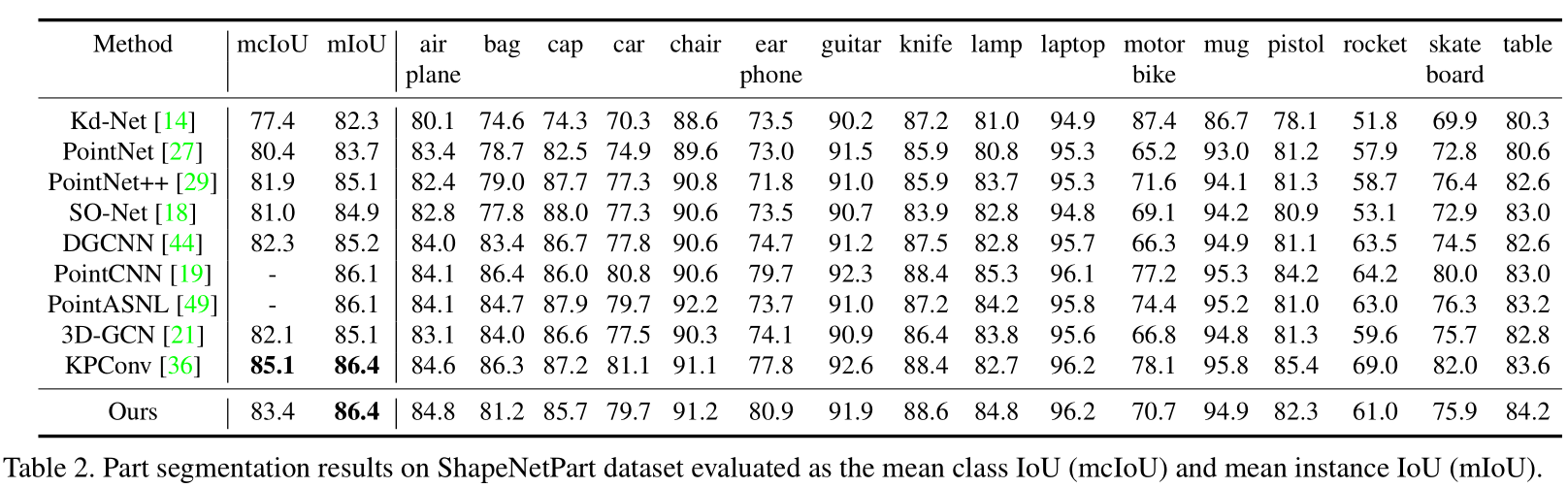
Part segmentation

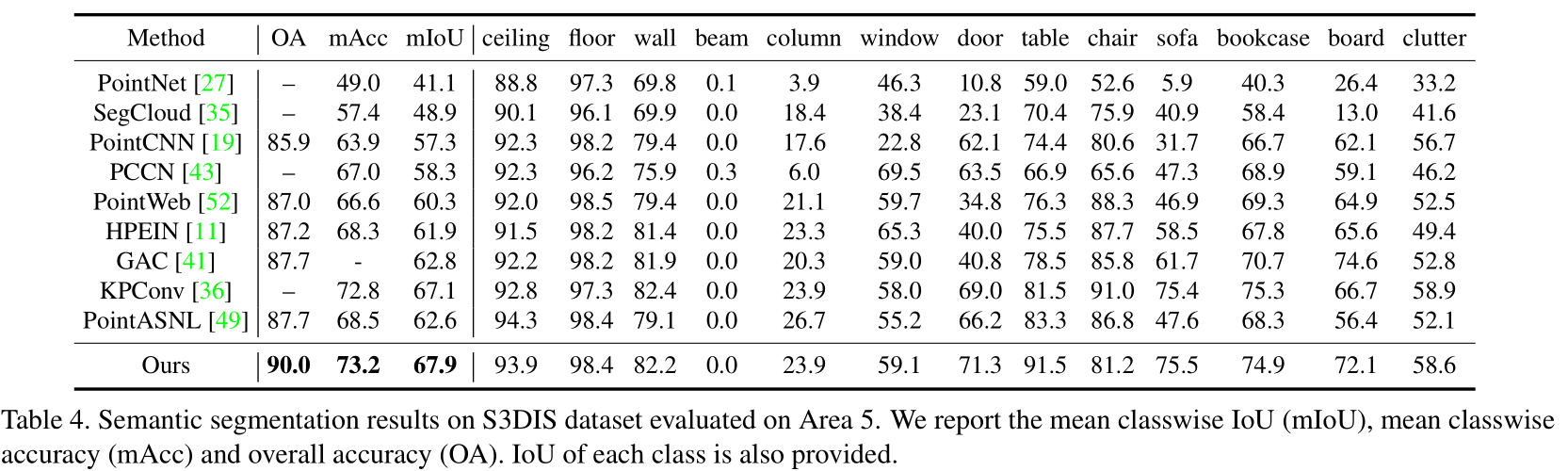
Indoor scene segmentation

Ablation studies

Adaptive convolution vs Fixed kernels & Feature decisions

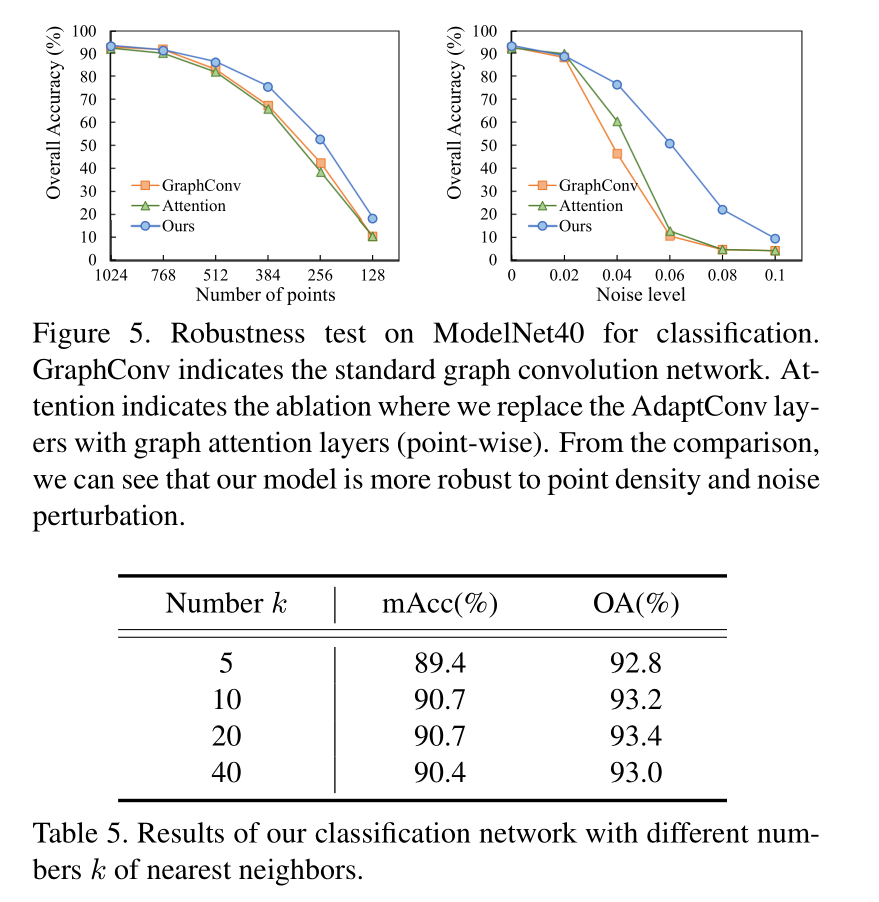
Robustness test

Efficiency

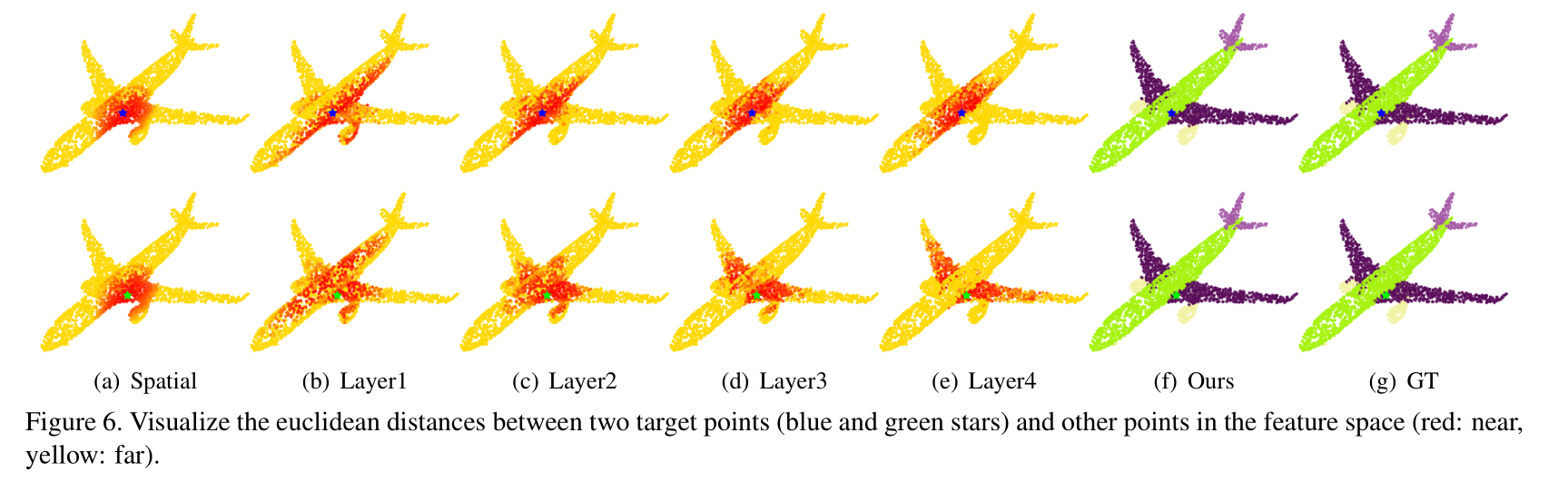
Visualization and learned features