44. 通配符匹配 ●●● ＆ HJ71 字符串通配符 ●●

44. 通配符匹配 ●●●

描述

给定一个字符串 (s) 和一个字符模式 § ，实现一个支持 '?' 和 '*' 的通配符匹配。

'?' 可以匹配任何单个字符。
'*' 可以匹配任意字符串（包括空字符串）。

两个字符串完全匹配才算匹配成功。

说明:
s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 ? 和 *。

示例

输入:
s = “aa”
p = “a”
输出: false
解释: “a” 无法匹配 “aa” 整个字符串。

---

输入:
s = “adceb”
p = “*a*b”
输出: true
解释: 第一个 ‘’ 可以匹配空字符串, 第二个 '’ 可以匹配字符串 “dce”.

题解

1. 动态规划

在给定的模式 p 中，只会有三种类型的字符出现：

• 小写字母 a−z，可以匹配对应的一个小写字母；
• 问号 ?，可以匹配任意一个小写字母；
• 星号 ∗，可以匹配任意字符串，可以为空，也就是匹配零或任意多个小写字母。

其中「小写字母」和「问号」的匹配是确定的，而「星号」的匹配是不确定的，因此我们需要枚举所有的匹配情况。为了减少重复枚举，我们可以使用动态规划来解决本题。

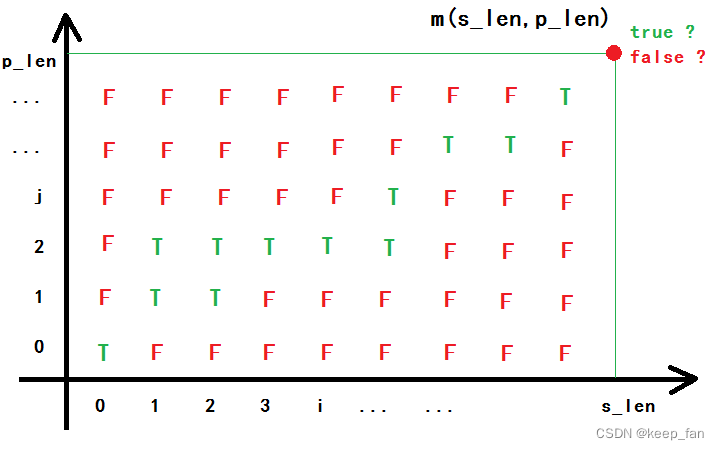
1. dp[i][j] 表示字符串 s 的前 j 个字符和模式 p 的前 i 个字符是否能匹配。

2. 边界初始化：
   dp[0][0] = true; 均为空字符进行匹配
   if(p[i-1] == '*') dp[i][0] = dp[i-1][0]; 连续*号开头可以对空字符进行匹配

3. 状态转移方程：
   – 如果p[i-1] == '*'：那么对s[j-1]没有要求，星号可以匹配任意个字符，因此状态转移分两种情况，即使用dp[i][j-1]或不使用dp[i-1][j]这个星号进行匹配：
   dp[i][j] = dp[i][j-1] | dp[i-1][j];
   – 其他情况则对单个字符进行一一匹配（dp[i-1][j-1] = true为前提）：
   dp[i][j] = dp[i-1][j-1] & (s[j-1] == p[i-1] | p[i-1] == '?');

4. 从前往后遍历，最终结果为dp[n1][n2]

• 时间复杂度：$O(mn)$，其中 m 和 n 分别是字符串 s 和模式 p 的长度。
• 空间复杂度：$O(mn)$，即为存储所有 (m+1)(n+1) 个状态需要的空间。此外，在状态转移方程中，由于 dp[i][j] 只会从 dp[i][…] 以及 dp[i−1][…] 转移而来，因此我们可以使用滚动数组对空间进行优化，即用两个长度为 m+1 的一维数组代替整个二维数组进行状态转移，空间复杂度为 O(m)。

class Solution {
    
public:
    bool isMatch(string s, string p) {
    
        int n1 = p.length(), n2 = s.length();
        if(n1 == 0 && n2 > 0) return false;
        vector<vector<bool>> dp(n1+1, vector<bool>(n2+1, false));
        dp[0][0] = true;                                // 初始化边界
        for(int i = 1; i <= n1; ++i){
    
            if(p[i-1] == '*') dp[i][0] = dp[i-1][0];    // 初始化边界，当开头出现连续的*时，dp[i][0] = true; 匹配0个字符
            for(int j = 1; j <= n2; ++j){
    
                if(p[i-1] == '*'){
                  // *号可以匹配任意个字母，用或不用*号匹配s[j-1]字符
                    dp[i][j] = dp[i][j-1] | dp[i-1][j];
                }else{
                              // 非*号，单个字符一一匹配
                    dp[i][j] = dp[i-1][j-1] & (s[j-1] == p[i-1] | p[i-1] == '?');
                }
            }
        }
        return dp[n1][n2];
    }
};

HJ71 字符串通配符 ●●

描述

在计算机中，通配符一种特殊语法，广泛应用于文件搜索、数据库、正则表达式等领域。

现要求各位实现字符串通配符的算法。

实现如下2个通配符：
*：匹配0个或以上的字符（注：能被*和?匹配的字符仅由英文字母和数字0到9组成，下同）
？：匹配1个字符

注意：匹配时不区分大小写。

数据范围：字符串长度：1 ≤ s ≤ 100

进阶：时间复杂度：$O(n^2)$ ，空间复杂度：$O(n)$

输入描述：

先输入一个带有通配符的字符串，再输入一个需要匹配的字符串

输出描述：

返回不区分大小写的匹配结果，匹配成功输出true，匹配失败输出false

示例

输入：
h*?*a
h#a
输出：
false
说明：
根据题目描述可知能被*和?匹配的字符仅由英文字母和数字0到9组成，所以?不能匹配#，故输出false

题解

1. 动态规划

与44. 通配符匹配 ●●●类似，不过本题字符串还包括了通配符无法进行匹配的符号字符，因此在用*号和?号匹配时要对匹配字符进行符号判断。

#include <string>
#include <iostream>
#include <vector>
using namespace std;

bool notSym(char ch){
    	// 非符号，即数字isdigit和字母isalpha
    return isdigit(ch) || isalpha(ch);
}

int main(){
    
    string s1, s2;
    while(cin >> s1 >> s2){
    
        int n1 = s1.length(), n2 = s2.length();
        vector<vector<bool>> dp(n1+1, vector<bool>(n2+1, false));
        dp[0][0] = true;
        for(int i = 1; i <= n1; ++i){
    
            dp[i][0] = dp[i-1][0] && (s1[i-1] == '*');    // 边界初始化，当开头出现连续的*时，dp[i][0] = true; 匹配0个字符
            for(int j = 1; j <= n2; ++j){
    
                if(s1[i-1] == '*'){
    
                	 // 当匹配字符为*号时，用或不用*号匹配s2[j-1]字符，*号匹配只能匹配notSym字符
                    dp[i][j] =  (dp[i][j-1] & notSym(s2[j-1])) | dp[i-1][j];     
                }else if(toupper(s1[i-1]) == toupper(s2[j-1]) || (s1[i-1] == '?' && notSym(s2[j-1]))){
        
                	// 字符一对一匹配，?号匹配只能匹配notSym字符
                    dp[i][j] = dp[i-1][j-1];
                }
            }
        }
        if(dp[n1][n2]){
    
            cout << "true" << endl;
        }else{
    
            cout << "false" << endl;
        }
    }
    return 0;
}