当前位置:网站首页>贝叶斯优化核极限学习机KELM用于回归预测
贝叶斯优化核极限学习机KELM用于回归预测
2022-08-04 15:53:00 【机器猫001】
0、前言
核极限学习机KELM因其强大学习能力和泛化性能在分类、回归预测问上备受青睐,本篇博文将仿真试验贝叶斯优化和极限学习机用于回归预测的效果,并与未优化的核极限学习机KELM、混合核极限学习机HKELM进行对比。
1、基本原理
1.1 KELM原理
KELM的原理本人在前期博客中有提到,请点击这里
KELM是一种核方法,将原始数据映射到高维核空间后,样本间的点积运算直接基于核函数就能实现。因此样本间的关系与核函数的选取有直接因果关系。常用核函数有:lin_kernel、poly_kernel、RBF_kernel ,wav_kernel,选择不同的核函数,需要确定的核参数也不同。
确定核函数后,核函数的计算结果直接受核参数设置的影响,采用优化算法确定最合适的参数。
1.2、混合核极限学习机HKELM原理
HKELM 顾名思义就是采用至少两个核函数而非单一核函数,目的是增强模型的泛化性能。因此在计算核矩阵时候需要计算两个核函数的值并进行加权求和。
3、实现效果
3.1 KELM回归预测实现
选定核函数,设定核参数:
%% 正则化系数与核参数进行设置
kernel='RBF_kernel';%核函数类型1.RBF_kernel 2.lin_kernel 3 poly_kernel
ker1=1;%RBF核的核参数
lambda=10; %正则系数 结果如下:
均方根误差rmse = 0.0115
平均绝对误差mae =0.0091
3.2 HKELM回归预测实现
选择两个核函数,并设置两个核函数各自对应的参数及权重占比
%% 正则化系数与核参数进行设置
kernel1='RBF_kernel';%核函数类型1.RBF_kernel 2.lin_kernel 3 poly_kernel
kernel2='poly_kernel';%核函数类型1.RBF_kernel 2.lin_kernel 3 poly_kernel
ker1=1;%RBF核的核参数
ker2=[1 2];%多项式核的核参数
lambda=10; %正则系数
w=0.5;%混合核里面rbf的权重,多项式核就是1-w 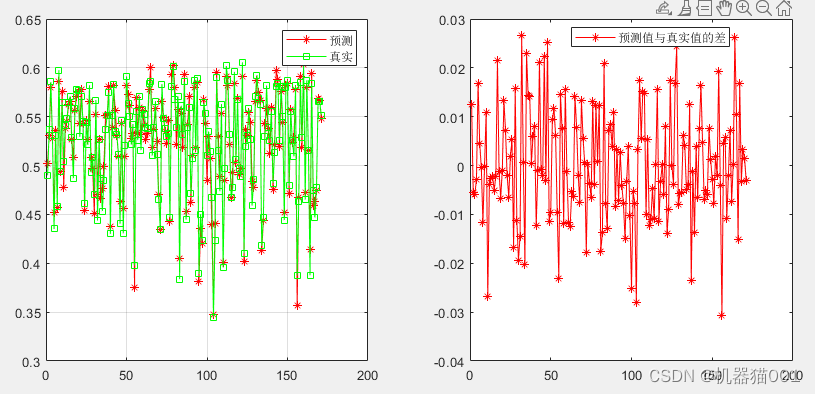
均方根误差
rmse =
0.0110
平均绝对误差
mae =
0.0085
3.3 贝叶斯优化核极限学习机回归预测实现
选取核函数,确定待优化核参数的范围,如下图所示:
% 核参数设置 详情看kernel_matrix
if strcmp(kernel1,'lin_kernel')
1;%如果是线性核 则没有核参数
elseif strcmp(kernel1,'RBF_kernel')
optimVars=[optimVars;
optimizableVariable('rbf',[1e-3 1e3]);];%如果是rbf核,则有一个核参数,范围是[1e-3 1e3]
elseif strcmp(kernel1,'poly_kernel')
optimVars=[optimVars;
optimizableVariable('poly1',[1e-3 1e3]);
optimizableVariable('poly2',[1 10],'Type','integer');];%如果是多项式核,则有2个核参数,且第二个是幂指数,取整
elseif strcmp(kernel1,'wav_kernel')
optimVars=[optimVars;
optimizableVariable('wav1',[1e-3 1e3]);
optimizableVariable('wav2',[1e-3 1e3]);
optimizableVariable('wav3',[1e-3 1e3])];%小波核有3个核参数
end 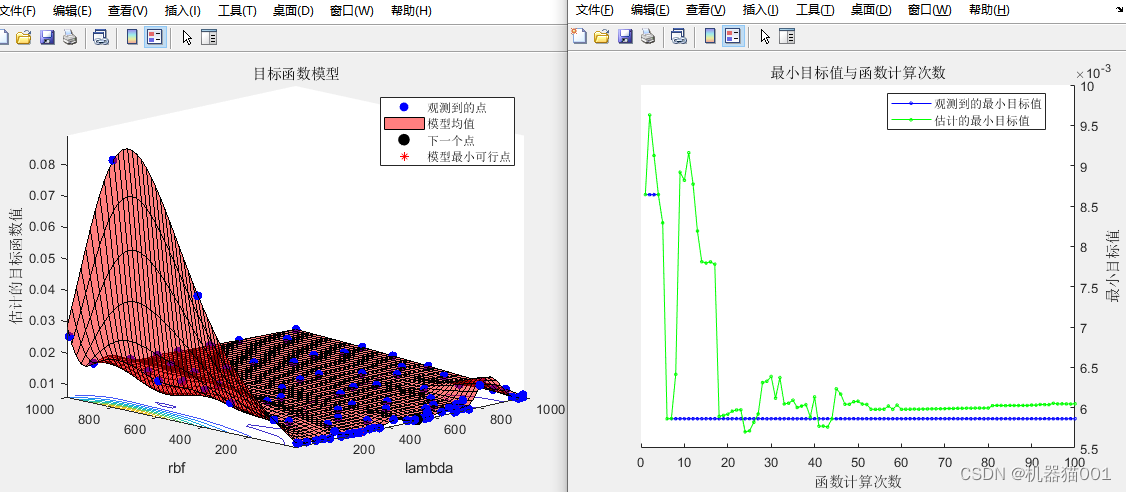

均方根误差
rmse =
0.0106
平均绝对误差
mae =
0.0082
4、对比分析
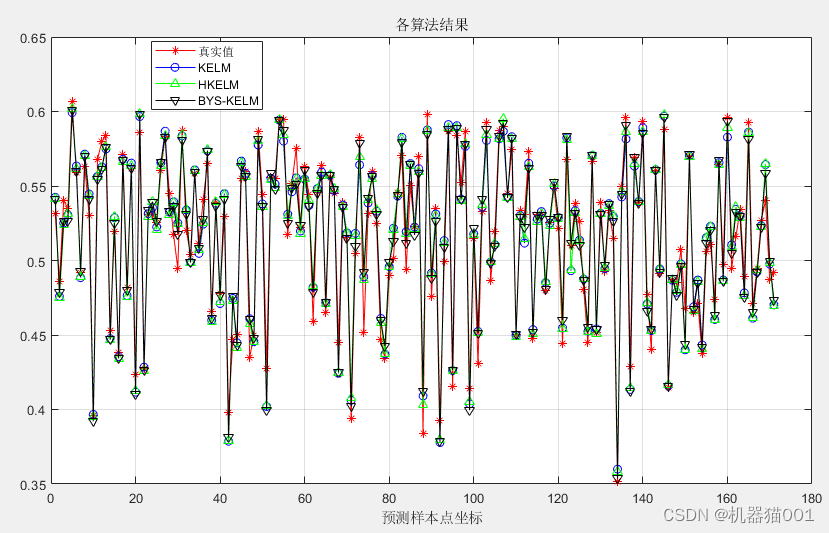
性能指标对比分析:
KELM
根均方差(RMSE):0.011518
平均绝对误差(MAE):0.0090813
平均相对百分误差(MAPE):1.8215%
R平方确定系数(R2):0.95494
HKELM
根均方差(RMSE):0.010991
平均绝对误差(MAE):0.0085007
平均相对百分误差(MAPE):1.6877%
R平方确定系数(R2):0.96041
BYS-KELM
根均方差(RMSE):0.01063
平均绝对误差(MAE):0.008195
平均相对百分误差(MAPE):1.6523%
R平方确定系数(R2):0.96162
边栏推荐
猜你喜欢
JVM Tuning-GC Fundamentals and Tuning Key Analysis
How to monitor code cyclomatic complexity by refactoring indicators
(2022杭电多校五)C - Slipper (dijkstra+虚拟结点)
LeetCode·每日一题·1403.非递增顺序的最小子序列·贪心

#夏日挑战赛# HarmonyOS 实现一个滑块验证

JVM调优-GC基本原理和调优关键分析

GPS卫星同步时钟,NTP网络同步时钟,北斗时钟服务器(京准)
A detailed explanation of what is software deployment
实战:10 种实现延迟任务的方法,附代码!
一文解答DevOps平台的制品库是什么
随机推荐
云存储硬核技术内幕——(11) 女子会所的秘密
吴恩达机器学习[12]-机器学习系统设计
云存储硬核技术内幕——小结(上)
Manacher(求解最长回文子串)
张乐:研发效能的黄金三角及需求与敏捷协作领域的实践
【Pick-in】Advertising-information flow cross-domain CTR estimation (to be updated)
GPS卫星同步时钟,NTP网络同步时钟,北斗时钟服务器(京准)
不需要服务器,教你仅用30行代码搞定实时健康码识别
Go 事,Gopher 要学的数字类型,变量,常量,运算符 ,第2篇
【Gopher 学个函数】边学边练,简单为 Go 上个分
全差分运放:THS4140
Crawler Xiaobai Notes (yesterday's supplement to pay attention to parsing data)
攻防视角下,初创企业安全实战经验分享
What is the difference between ITSM software and a work order system?
解决dataset.mnist无法加载进去的情况
《2022 年上半年全球独角兽企业发展研究报告》发布——DEMO WORLD世界创新峰会圆满落幕
Difference between GET and POST requests
你一定从未看过如此通俗易懂的YOLO系列(从v1到v5)模型解读
MySQL select加锁分析
What is an artifact library in a DevOps platform?What's the use?