当前位置:网站首页>AcWing 2811. 最长公共子串(后缀自动机 fa 指针的性质)
AcWing 2811. 最长公共子串(后缀自动机 fa 指针的性质)
2022-08-02 07:20:00 【Morgannr】

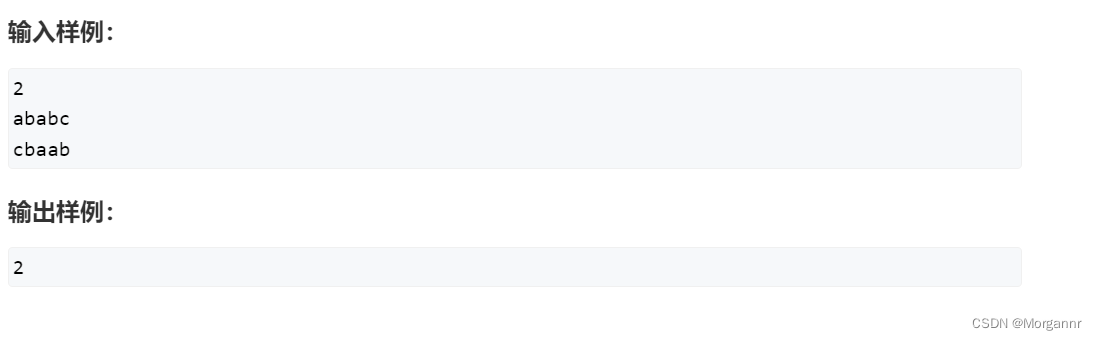
题意:
给定 n 行字符串,求出所有字符串的 最长公共子串。
思路:
先想想如果是 两个串 的话,如何解决这个问题?
现在我们有 A、B 两个串,我们 先把 A 串建成后缀自动机(相当于 将 A 的所有子串 都扔进一个 哈希表 中,即 快速查询 A 的每个子串),
想想 暴力 怎么做:
- 枚举
B串中每个子串的起点i,从 起点i开始 往后走,边走边 在后缀自动机A中查询,直到走到 某一个位置 发现 “加上一个字符之后,A的自动机中不存在该串”,就说明此时我们找到了一个 以i为起点,长度最大的一个公共子串,停下来即可。这样一来,我们就枚举了 其中一个起点。之后我们 将起点往后挪动一位,再 往后 进行 枚举,以此类推,这样的算法是一定可以将 所有的情况(任意起点在A中出现的最长子串)枚举到的。最后,对于每个起点求出来的最长子串长度取max,即为答案。
现在考虑如何 优化这个算法,这就要用到 SAM 的性质 了,
- 当我们在
SAM中走到 状态p(节点),我们知道 节点p是具有一些子串(后缀)的,且都是 连续的,且为 最长子串的后缀。p之后不存在一个字符,意味着 其包含的所有子串后方都不能接新的字符。此时,我们试着 将起点往后挪一位,但这样可能还是会在SAM中走到p节点,且 没有新的出边(此时 得到的新的公共子串长度还没有上一轮得到的长度更长,且属于p节点代表的同类子串集合)。思考一下,起点 挪动到什么时候才会有 质变 呢?可以想到,当 起点 为p节点代表子串集合中最短串首字符时,将起点 往后挪一位,这时才会有 质变,即 走到p时有了新的出边,也就是可能将 答案更新,相当于 将p代表子串集合中最短串首位删除,删除之后的状态我们应该很熟悉了,其实就是p用绿色链接边连向的节点。 - 总结一下:优化之处 在于,可以直接 将起点跳转至
p绿色链接边连向的点p' = fa[p],如果 跳转至p'之后 后方还是 没有出边,那么 继续跳转至fa[p']即可,显然这个过程时会 结束 的(跳转至 有出边的节点 或 空字符串),这样一来我们就 省去了挨个暴力枚举,起到了将时间复杂度优化的效果(优化成了O(n)),这一连串的 匹配过程 和KMP有惊人的相似之处。
考虑如何 将答案记录,
- 显然可以 在
SAM中的每个状态p中都记录一个最大值now[p],表示 当前在B和 状态p中都出现过的最长子串长度,由于A的子串必然被划分到了每一个状态p中,那么,对于 每个状态的now[p]联合起来取最大值,就可以 将A的所有子串的遍历一遍,即求出A的所有子串中,哪一个子串 是 在B中出现过 且 长度最长 的。
至此,对于 两串求最长公共子串的做法 已经分析完毕,现在想想对于 n 个字符串 该如何处理?
- 先将 第
1个串 建成SAM,之后对于 第2个串 进行一遍刚刚分析的操作,这样一来,对于 每一个状态p,都可以 求出其now2[p],当求 第3个串 时,我们可以求出 所有now3[p],当求 第n个串 时我们可以求出nown[p],对于 状态p的最长公共子串 我们取的应为ans_p = min(now1[p], now2[p], ..., nown[p]),而对于 最终答案(n个串 的 最长公共子串),我们是 以状态p为变量,取ans = max(ans_p1, ans_p2, ..., ans_pm)。
代码:
#include <bits/stdc++.h>
using namespace std;
//#define map unordered_map
//#define int long long
const int N = 1e4 + 10, M = N << 1;
int n;
int tot = 1, np = 1;
char s[N];
int ch[M][26], fa[M], cnt[M], len[M];
int ans[M], now[M];
int h[M], e[M], ne[M], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void extend(int c) {
int p = np;
np = ++tot;
len[np] = len[p] + 1, cnt[np] = 1;
while (p && !ch[p][c]) {
ch[p][c] = np;
p = fa[p];
}
if (!p) {
fa[np] = 1;
}
else {
int q = ch[p][c];
if (len[q] == len[p] + 1) fa[np] = q;
else {
int nq = ++tot;
len[nq] = len[p] + 1;
fa[nq] = fa[q], fa[q] = fa[np] = nq;
while (p && ch[p][c] == q) {
ch[p][c] = nq;
p = fa[p];
}
memcpy(ch[nq], ch[q], sizeof ch[q]);
}
}
}
void dfs(int u) {
for (int i = h[u]; ~i; i = ne[i]) {
dfs(e[i]);
now[u] = max(now[u], now[e[i]]);
}
}
signed main()
{
cin >> n >> s;
for (int i = 0; s[i]; ++i) {
extend(s[i] - 'a');
}
for (int i = 1; i <= tot; ++i) {
ans[i] = len[i];
}
memset(h, -1, sizeof h);
for (int i = 2; i <= tot; ++i) {
add(fa[i], i);
}
for (int i = 0; i < n - 1; ++i) {
scanf("%s", s);
memset(now, 0, sizeof now);
int p = 1, t = 0; //从起点p=1开始,t为当前长度
for (int j = 0; s[j]; ++j) {
int c = s[j] - 'a';
while (p > 1 && !ch[p][c]) {
//当p不是头结点,且p没有c这个儿子
p = fa[p], t = len[p]; //p往后挪 t取跳转到的状态的最长值
}
if (ch[p][c]) p = ch[p][c], ++t; //如果p有c这条边,那么跳过去,当前长度+1
now[p] = max(now[p], t);
}
dfs(1);
//当前串求完所有now后,枚举所有状态ans存储所有状态最小值
for (int j = 1; j <= tot; ++j) ans[j] = min(ans[j], now[j]);
}
int res = 0;
for (int i = 1; i <= tot; ++i) res = max(res, ans[i]);
printf("%d\n", res);
return 0;
}
边栏推荐
- CSRF-Cross-site request forgery-related knowledge
- A Preliminary Study on the Basic Principles of Formal Methods
- Splunk Filed extraction field interception
- ROS file system and related commands
- OC-NSDictionary
- 静态路由综合实验
- 初探形式化方法基本原理
- spark read folder data
- Introduction to mysql operation (4) ----- data sorting (ascending, descending, multi-field sorting)
- flutter 自己写一个组件
猜你喜欢

(2022 Niu Ke Duo School 5) D-Birds in the tree (tree DP)

DeadLock的可视化分析

如何保护智能家居不受黑客攻击
![MySQL error 1055 solution: [Err] 1055 - Expression #1 of ORDER BY clause is not in GROUP BY clause and contains](/img/aa/ab58ec47bb96df803dbc6a8ff6dde3.png)
MySQL error 1055 solution: [Err] 1055 - Expression #1 of ORDER BY clause is not in GROUP BY clause and contains

论文理解:“Cross-Scale Residual Network: A GeneralFramework for Image Super-Resolution,Denoising, and “

MySQL - Detailed Explanation of Database Transactions
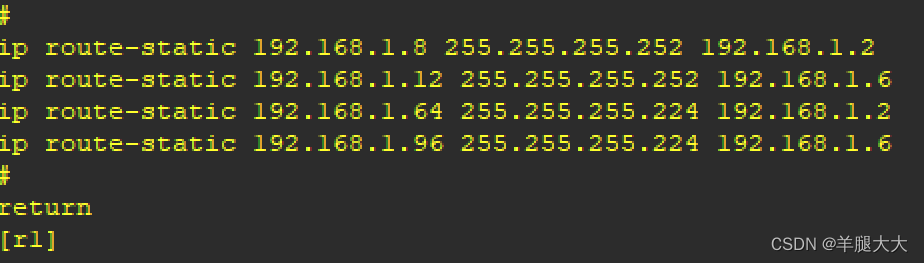
静态路由综合实验
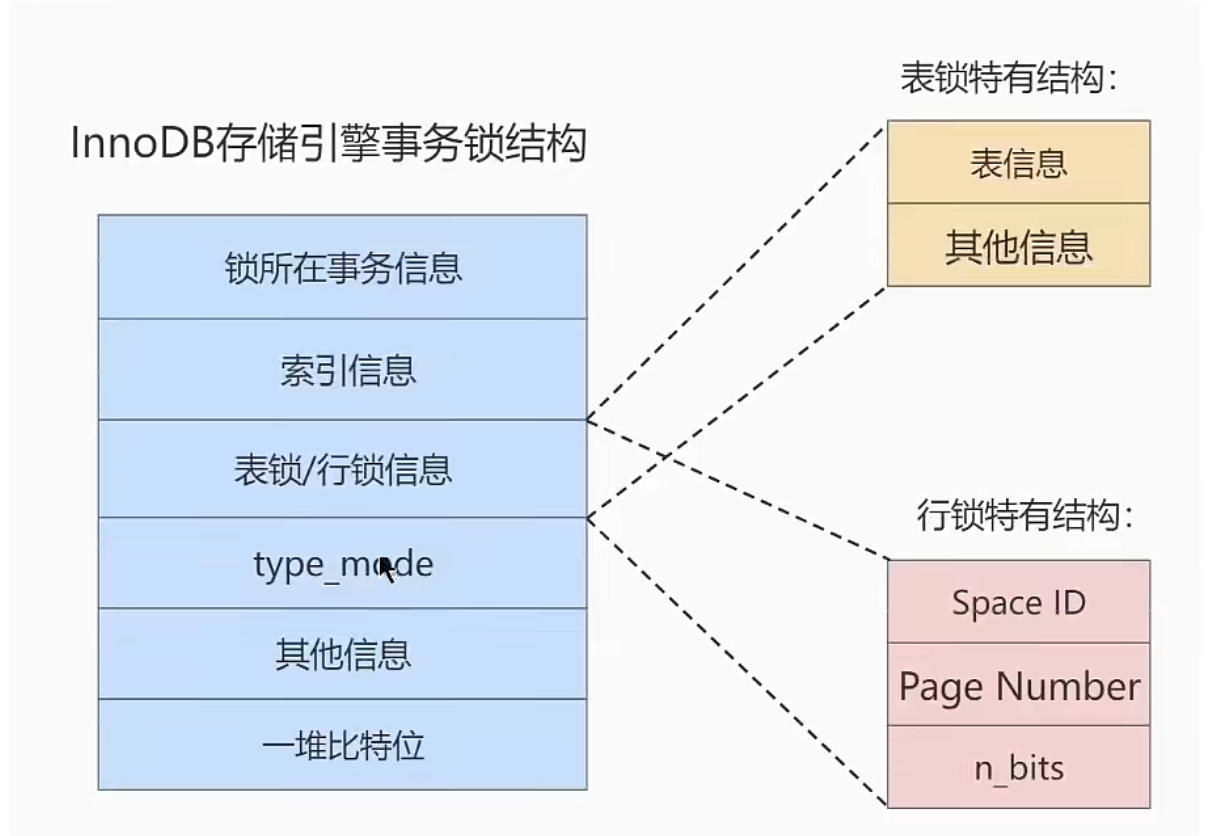
MySQL - locking mechanism

MySQL-慢查询日志

59: Chapter 5: Develop admin management services: 12: MongoDB usage scenarios; (non-core data, non-core data with a relatively large amount of data, small private files such as face photos;)
随机推荐
初探形式化方法基本原理
HCIP 第十三天
Understand Chisel language. 31. Chisel advanced communication state machine (3) - Ready-Valid interface: definition, timing and implementation in Chisel
Debian 10 dhcp relay (dhcp 中继) dhcp 固定分配
【Unity3D】初学加密技巧(反破解)
CSRF-Cross-site request forgery-related knowledge
How to export multiple query results at once in SQL server 2014?
LeetCode 2360. The longest cycle in a graph
论文理解:“Cross-Scale Residual Network: A GeneralFramework for Image Super-Resolution,Denoising, and “
Thesis understanding: "Cross-Scale Residual Network: A GeneralFramework for Image Super-Resolution, Denoising, and "
flutter解决键盘和输入框不适配问题
postgres 水平分表,自动创建分区,按时间分表
pnpm + workspace + changesets 构建你的 monorepo 工程
Inverter insulation detection detection function and software implementation
MySQL-数据库事务详解
Splunk Field Caculated 计算字段
Appium swipe problem
HCIP 第八天
MySQL-数据库设计规范
redis-高级篇