当前位置:网站首页>math_泰勒公式
math_泰勒公式
2022-07-03 18:52:00 【xuchaoxin1375】
文章目录
微分泰勒公式
用一个容易计算/结构简单的函数来来近似的表达一个复杂的函数,这中近似表达在数学上称为逼近
泰勒公式使用使用多项式 P P P(polynominal)来逼近一个给定函数 f ( x ) f(x) f(x);
我们用 P i P_i Pi来描述逼近 f ( x ) f(x) f(x)的过程:
一阶近似:
- P 1 = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) = a 0 + a 1 ( x − x 0 ) P_1=f(x_0)+f'(x_0)(x-x_0) =a_0+a_1(x-x_0) P1=f(x0)+f′(x0)(x−x0)=a0+a1(x−x0)
二阶近似:
- P 2 = a 0 + a 1 ( x − x 0 ) + a 2 ( x − x 0 ) 2 P_2=a_0+a_1(x-x_0)+a_2(x-x_0)^2 P2=a0+a1(x−x0)+a2(x−x0)2
…(更高精度的逼近函数)
问题是,如何确定系数 a i a_i ai
i 阶 逼 近 函 数 P i i阶逼近函数P_i i阶逼近函数Pi
i 阶 逼 近 函 数 P i 表 示 为 多 项 式 : P i = a 0 + ∑ k = 1 n a k ( x − x 0 ) k ; = f ( x 0 ) + ∑ k = 1 n a k ( x − x 0 ) k ; i阶逼近函数P_i表示为多项式: \\P_i =a_0+ \sum\limits_{k=1}^{n} {a_k}(x-x_0)^{k}; \\=f(x_0)+\sum\limits_{k=1}^{n} {a_k}(x-x_0)^{k}; i阶逼近函数Pi表示为多项式:Pi=a0+k=1∑nak(x−x0)k;=f(x0)+k=1∑nak(x−x0)k;
而 公 式 ∑ k = 0 n a k ( x − x 0 ) k 会 在 x = x 0 出 发 生 异 常 , 出 现 0 0 的 项 , 因 此 独 立 拆 分 出 来 a 1 , 使 得 各 项 的 指 数 至 少 为 1 但 是 , 可 以 写 作 : ( 注 意 累 加 下 界 k = 0 ) { ∑ k = 0 n a k ( x − x 0 ) k ; x ≠ x 0 f ( x 0 ) ; x = x 0 \\而公式 \bcancel{ \sum\limits_{k=0}^{n} {a_k}(x-x_0)^{k} } \\会在x=x_0出发生异常,出现0^0的项,因此独立拆分出来a_1,使得各项的指数至少为1 \\但是,可以写作:(注意累加下界k=0) \begin{cases} \sum\limits_{k=0}^{n} {a_k}(x-x_0)^{k};x\neq x_0 \\ f(x_0);x=x_0 \end{cases} 而公式k=0∑nak(x−x0)k会在x=x0出发生异常,出现00的项,因此独立拆分出来a1,使得各项的指数至少为1但是,可以写作:(注意累加下界k=0)⎩⎨⎧k=0∑nak(x−x0)k;x=x0f(x0);x=x0
函 数 P i 和 f ( x ) 的 导 数 之 间 有 如 下 约 束 : n 阶 的 逼 近 函 数 P n 和 被 逼 近 函 数 f ( x ) 在 点 x 0 的 ( i 阶 ) 导 数 值 相 同 ( i ∈ [ 0 , N ] ; i ∈ N ∗ ) ) 函数P_i和f(x)的导数之间有如下约束: \\n阶的逼近函数P_n和被逼近函数f(x)在点x_0的(i阶)导数值相同(i\in[0,N] ;i\in N^*)) 函数Pi和f(x)的导数之间有如下约束:n阶的逼近函数Pn和被逼近函数f(x)在点x0的(i阶)导数值相同(i∈[0,N];i∈N∗))
P n ( i ) ( x 0 ) = f ( i ) ( x 0 ) (cf (constraint family(i)) \\P_n^{(i)}{(x_0)}=f^{(i)}{(x_0)} \tag{cf\ (constraint family(i)} Pn(i)(x0)=f(i)(x0)(cf (constraint family(i))
这 里 将 i ∈ N ∗ 的 各 个 i 值 带 入 上 式 ( c f ) , 可 以 得 到 一 系 列 的 约 束 等 式 , 每 个 等 式 可 以 求 解 出 一 个 项 a i , a i 是 关 于 f ( i ) 的 表 达 式 这里将i\in N^*的各个i值带入上式(cf),可以得到一系列的约束等式, \\每个等式可以求解出一个项a_i,a_i是关于f^{(i)}的表达式 这里将i∈N∗的各个i值带入上式(cf),可以得到一系列的约束等式,每个等式可以求解出一个项ai,ai是关于f(i)的表达式
对于 ( x + a ) n (x+a)^n (x+a)n形式的高阶导数
( x n ) ( n ) = n ! ; ( x n ) ( n + 1 ) = 0 可 以 得 到 ( ( x + a ) n ) ( n ) = ( ∑ i = 0 n x i a n − i ) ) ( n ) = 1 ⋅ ( x n ) ( n ) = n ! (x^n)^{(n)}=n!; \\(x^n)^{(n+1)}=0 \\可以得到 \\ ((x+a)^n)^{(n)} =(\sum\limits_{i=0}^{n}{x^{i}a^{n-i}}))^{(n)}=1\cdot (x^{n})^{(n)}=n! (xn)(n)=n!;(xn)(n+1)=0可以得到((x+a)n)(n)=(i=0∑nxian−i))(n)=1⋅(xn)(n)=n!
更 一 般 的 , 我 们 可 以 推 导 : 记 y = ( x + a ) n ( ( x + a ) n ) ( k ) = y ( k ) 1 ⩽ k ⩽ n ; k , n ∈ N + 时 , ( ( x + a ) n ) ( k ) = n ! ( n − k ) ! ( x + a ) n − k = P n k ( x + a ) n − k 更一般的,我们可以推导: \\ 记y=(x+a)^n \\ ((x+a)^n)^{(k)}=y^{(k)} \\1\leqslant k\leqslant n;k,n\in N^+时, \\((x+a)^n)^{(k)}=\frac{n!}{(n-k)!}(x+a)^{n-k} =P^{k}_{n}{(x+a)}^{n-k} 更一般的,我们可以推导:记y=(x+a)n((x+a)n)(k)=y(k)1⩽k⩽n;k,n∈N+时,((x+a)n)(k)=(n−k)!n!(x+a)n−k=Pnk(x+a)n−k
特 别 的 , 当 k = n 时 , ( 常 数 a 的 值 在 此 时 无 关 紧 要 ) 便 得 : ( ( x + a ) n ) ( n ) = n ! \\特别的,当k=n时,(常数a的值在此时无关紧要) 便得: \\((x+a)^n)^{(n)}=n! 特别的,当k=n时,(常数a的值在此时无关紧要)便得:((x+a)n)(n)=n!
P i 的 k 阶 导 数 P_i的k阶导数 Pi的k阶导数
P i ( x ) = a 0 + ∑ k = 1 n a k ( x − x 0 ) k ; P_i(x)=a_0+\sum\limits_{k=1}^{n} {a_k}(x-x_0)^{k}; Pi(x)=a0+k=1∑nak(x−x0)k;
对 于 i 阶 逼 近 函 数 P i , 对 其 求 k 阶 导 数 ; P i ( k ) ( x 0 ) = 0 + ∑ 0 + a k k ! + ∑ 0 = a k k ! 根 据 约 束 条 件 = f ( k ) ( x 0 ) 从 而 得 到 a k = f ( k ) ( x 0 ) k ! 对于i阶逼近函数P_i,对其求k阶导数; \\ P_i^{(k)}(x_0)=0+\sum\limits0+a_{k}k!+\sum\limits0=a_kk! \\ 根据约束条件 \\=f^{(k)}{(x_0)} \\从而得到a_k=\frac{f^{(k)}{(x_0)}}{k!} 对于i阶逼近函数Pi,对其求k阶导数;Pi(k)(x0)=0+∑0+akk!+∑0=akk!根据约束条件=f(k)(x0)从而得到ak=k!f(k)(x0)
泰勒多项式 P n P_n Pn 函 数 f ( x ) 在 点 x = x 0 处 的 n 次 T a y l o r 多 项 式 函数f(x)在点x=x_0处的\mathbb{n次Taylor多项式} 函数f(x)在点x=x0处的n次Taylor多项式
a k : 逼 近 函 数 P i 各 项 系 数 a k 的 值 a_k:逼近函数P_i各项系数a_k的值 ak:逼近函数Pi各项系数ak的值
f ( x ) 的 在 x = x 0 处 ( 即 f ( x 0 ) ) 的 i 阶 逼 近 函 数 P i 表 示 为 多 项 式 : f ( x ) ≈ P n ( x ) P n ( x , x 0 ) = a 0 + ∑ k = 1 n a k ( x − x 0 ) k ; f(x)的在x=x_0处(即f(x_0))的i阶逼近函数P_i表示为多项式: \\f(x)\approx P_n{(x)} \\P_n(x,x_0)=a_0+\sum\limits_{k=1}^{n} {a_k}(x-x_0)^{k}; \\ f(x)的在x=x0处(即f(x0))的i阶逼近函数Pi表示为多项式:f(x)≈Pn(x)Pn(x,x0)=a0+k=1∑nak(x−x0)k;
该 式 子 称 为 : 函 数 f ( x ) 在 点 x = x 0 处 的 n 次 T a y l o r 多 项 式 , 或 者 称 为 f ( x ) 按 ( x − x 0 ) 的 幂 展 开 的 n 次 泰 勒 多 项 式 \\该式子称为:函数f(x)在点x=x_0处的\mathbb{n次Taylor多项式}, \\或者称为f(x)按(x-x_0)的幂展开的n次泰勒多项式 \\ 该式子称为:函数f(x)在点x=x0处的n次Taylor多项式,或者称为f(x)按(x−x0)的幂展开的n次泰勒多项式
a k = f ( k ) ( x 0 ) k ! a_k=\frac{f^{(k)}{(x_0)}}{k!} ak=k!f(k)(x0)
系数特点
可见, a k a_k ak 是 关 于 f ( x ) 在 x 0 处 的 k 阶 导 数 f ( k ) ( x 0 ) z 以 及 k ! 的 表 达 式 是关于f(x)在x_0处的k阶导数f^{(k)}(x_0)z以及k!的表达式 是关于f(x)在x0处的k阶导数f(k)(x0)z以及k!的表达式
多项式中的各项系数有相同的特点:包含两个部分
- k阶导
- k阶乘
通项
最 后 , 系 数 再 乘 以 核 心 式 ( x − x 0 ) 的 k 次 幂 ( x − x 0 ) k 最后,系数再乘以核心式(x-x_0)的k次幂(x-x_0)^k 最后,系数再乘以核心式(x−x0)的k次幂(x−x0)k,得到一个完整的泰勒多项式通项:
a k ( x − x 0 ) ( k ) = f ( k ) ( x 0 ) k ! × ( x − x 0 ) k a_k(x-x_0)^{(k)}=\frac{f^{(k)}{(x_0)}}{k!}\times(x-x_0)^{k} ak(x−x0)(k)=k!f(k)(x0)×(x−x0)k
general term formula
T ( x 0 , k , ξ ) = a k ( x − x 0 ) ( k ) = f ( k ) ( x 0 ) k ! × ( x − x 0 ) k R n ( x ) = T ( x 0 , n + 1 , ξ ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 T(x_0,k,\xi)=a_k(x-x_0)^{(k)}=\frac{f^{(k)}{(x_0)}}{k!}\times(x-x_0)^{k} \\ R_n(x)=T(x_0,n+1,\xi)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} T(x0,k,ξ)=ak(x−x0)(k)=k!f(k)(x0)×(x−x0)kRn(x)=T(x0,n+1,ξ)=(n+1)!f(n+1)(ξ)(x−x0)n+1
R n ( x ) R_n(x) Rn(x):余项(误差描述函数)
- 注意到, 余 项 R n ( x ) 也 是 函 数 , 所 以 可 以 想 象 , 逼 近 函 数 P n ( x ) 在 估 算 f ( x ) 的 不 同 点 函 数 值 , 可 有 不 同 的 精 确 程 度 余项R_n(x)也是函数,所以可以想象,逼近函数P_n(x)在估算f(x)的不同点函数值,可有不同的精确程度 余项Rn(x)也是函数,所以可以想象,逼近函数Pn(x)在估算f(x)的不同点函数值,可有不同的精确程度
余项的类型
余项有两种:
拉格朗日(Lagrange)型余项
余项和taylor多项式中的各项系数有相同的特点:包含三个部分
k阶导,
k次幂,
k阶乘
R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 余 项 的 系 数 部 分 f ( n + 1 ) ( ξ ) ( n + 1 ) ! 与 普 通 系 数 相 比 : { x 0 → ξ n → ( n + 1 ) R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}{(x-x_0)^{n+1}} \\余项的系数部分\frac{f^{(n+1)}(\xi)}{(n+1)!} \\与普通系数相比: \\ \begin{cases} x_0\rightarrow \xi \\n\rightarrow (n+1) \end{cases} Rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1余项的系数部分(n+1)!f(n+1)(ξ)与普通系数相比:{ x0→ξn→(n+1)
佩亚诺(Peano)型余项
Largrange型的简化描述(高阶无穷小)
R n ( x ) = o ( ( x − x 0 ) n ) \\R_n(x)=o((x-x_0)^n) Rn(x)=o((x−x0)n)
公式宏定义(部分编辑器不支持,则导致公式无法渲染,typora 支持)
\def\ltzero{\lim_{x\rightarrow 0}} \def\ltxzero#1{\lim_{x\rightarrow x_0}} \def\ltx#1{\lim_{x\rightarrow #1}} \def\ltxi#1{\lim_{x\rightarrow x_{#1}}} \def\limtoxi#1{\lim_{x\rightarrow x_{#1}}} \def\Rn#1{R_n^{(#1)}(x)}
记:
R n ( x ) = f ( x ) − P n ( x ) R_n(x)=f(x)-P_n(x) Rn(x)=f(x)−Pn(x)
P n ( i ) ( x 0 ) = f ( i ) ( x 0 ) 即 : f ( i ) ( x 0 ) − p n ( i ) ( x 0 ) = 0 (cf (constraint family)) \\P_n^{(i)}{(x_0)}=f^{(i)}{(x_0)} \tag{cf\ (constraint family)} \\即: \\ f^{(i)}{(x_0)}- p_n^{(i)}{(x_0)}=0 Pn(i)(x0)=f(i)(x0)即:f(i)(x0)−pn(i)(x0)=0(cf (constraint family))
R n ( i ) ( x 0 ) = f ( i ) ( x ) − P n ( i ) ( x ) = 0 即 , R n ( x 0 ) = R n ′ ( x 0 ) = R n ′ ′ ( x 0 ) = ⋯ = R n ( n ) ( x 0 ) R_n^{(i)}(x_0)=f^{(i)}{(x)}-P_n^{(i)}{(x)}=0 \\ 即,R_n(x_0)=R_n^{'}(x_0)=R_n^{''}(x_0)=\cdots=R_n^{(n)}(x_0) Rn(i)(x0)=f(i)(x)−Pn(i)(x)=0即,Rn(x0)=Rn′(x0)=Rn′′(x0)=⋯=Rn(n)(x0)
余项和无穷小的关系
R n ( n ) ( x 0 ) = o ( ( x − x 0 ) n ) \def\ltzero{\lim_{x\rightarrow 0}} \def\ltxzero#1{\lim_{x\rightarrow x_0}} \def\ltx#1{\lim_{x\rightarrow #1}} \def\ltxi#1{\lim_{x\rightarrow x_{#1}}} \def\limtoxi#1{\lim_{x\rightarrow x_{#1}}} \def\Rn#1{R_n^{(#1)}(x)} \\R_n^{(n)}(x_0)=o((x-x_0)^n) Rn(n)(x0)=o((x−x0)n)
∵ ( 反 复 使 用 洛 必 达 法 则 ) lim x → x 0 R n ( x ) ( x − x 0 ) n = lim x → x 0 R n ′ ( x ) n ( x − x 0 ) n − 1 = lim x → x 0 R ′ ′ ( x ) n ( n − 1 ) ( x − x 0 ) n − 2 = ⋯ = lim x → x 0 R n ( n − 1 ) ( x ) n ! ( x − x 0 ) = 1 n ! lim x → x 0 R n ( n − 1 ) ( x ) − R n ( n − 1 ) ( x 0 ) x − x 0 = 1 n ! R n ( n ) ( x 0 ) = 0 \def\ltzero{\lim_{x\rightarrow 0}} \def\ltxzero#1{\lim_{x\rightarrow x_0}} \def\ltx#1{\lim_{x\rightarrow #1}} \def\ltxi#1{\lim_{x\rightarrow x_{#1}}} \def\limtoxi#1{\lim_{x\rightarrow x_{#1}}} \def\Rn#1{R_n^{(#1)}(x)} \\ \because(反复使用洛必达法则) \lim\limits_{x\rightarrow x_0}{\frac{R_n{(x)}}{(x-x_0)^n}} =\lim\limits_{x\rightarrow x_0}{\frac{R^{'}_n(x)}{n(x-x_0)^{n-1}}} \\ =\ltxi{0} {\frac{R^{''}{(x)}}{n(n-1)(x-x_0)^{n-2}}} =\cdots \\=\ltxi{0}{\frac{R_n^{(n-1)}(x)}{n!(x-x_0)}} =\frac{1}{n!}\ltxi{0}{\frac{\Rn{n-1}-R_n^{(n-1)}(x_0)}{x-x_0}} =\frac{1}{n!}R_n^{(n)}(x_0)=0 \\ ∵(反复使用洛必达法则)x→x0lim(x−x0)nRn(x)=x→x0limn(x−x0)n−1Rn′(x)=x→x0limn(n−1)(x−x0)n−2R′′(x)=⋯=x→x0limn!(x−x0)Rn(n−1)(x)=n!1x→x0limx−x0Rn(n−1)(x)−Rn(n−1)(x0)=n!1Rn(n)(x0)=0
- 其中,极限转换为导数的过程:
记 g ( x ) = R n ( n − 1 ) ( x ) ; 由 于 前 面 的 论 述 可 知 R n ( i ) ( x 0 ) = 0 , 则 , g ( x 0 ) = 0 由 导 数 的 定 义 g ′ ( x 0 ) = lim x → x 0 g ( x ) − g ( x 0 ) x − x 0 则 R n ( n ) ( x 0 ) = g ′ ( x 0 ) \def\ltzero{\lim_{x\rightarrow 0}} \def\ltxzero#1{\lim_{x\rightarrow x_0}} \def\ltx#1{\lim_{x\rightarrow #1}} \def\ltxi#1{\lim_{x\rightarrow x_{#1}}} \def\limtoxi#1{\lim_{x\rightarrow x_{#1}}} \def\Rn#1{R_n^{(#1)}(x)} \\记g(x)=\Rn{n-1};由于前面的论述可知R_{n}^{(i)}{(x_0)}=0,则,g(x_0)=0 \\由导数的定义g'(x_0)=\limtoxi{0}{\frac{g(x)-g(x_0)}{x-x_0}} \\ 则R_n^{(n)}(x_0)=g'(x_0) 记g(x)=Rn(n−1)(x);由于前面的论述可知Rn(i)(x0)=0,则,g(x0)=0由导数的定义g′(x0)=x→x0limx−x0g(x)−g(x0)则Rn(n)(x0)=g′(x0)
| R n ( i ) ( x ) R^{(i)}_n(x) Rn(i)(x)导数阶数i | 1 | 2 | 3 | … | n | |
|---|---|---|---|---|---|---|
| 对应i阶导数的( ( x − x 0 ) n ) ( i ) (x-x_0)^n)^{(i)} (x−x0)n)(i)累乘系数因子 | n | n-(1) | n-(2) | … | n-(n-1)=1 |
泰勒公式
f ( x ) = P n ( x ) + R n ( x ) 从 程 序 设 计 的 角 度 , 为 了 强 调 x 0 对 公 式 的 影 响 , 可 以 写 作 * f ( x ) = g ( x , x 0 , ξ ) = P n ( x , x 0 ) + R n ( x , x 0 , ξ ) ; ( c o n s t a n t ξ ∈ ( x 0 , x ) ) f(x)=P_n(x)+R_n(x) \\从程序设计的角度,为了强调x_0对公式的影响,可以写作 \\\bigstar\ f(x)=g(x,x_0,\xi)=P_n(x,x_0)+R_n(x,x_0,\xi);(constant\ \xi \in (x_0,x)) f(x)=Pn(x)+Rn(x)从程序设计的角度,为了强调x0对公式的影响,可以写作* f(x)=g(x,x0,ξ)=Pn(x,x0)+Rn(x,x0,ξ);(constant ξ∈(x0,x))
f ( x ) = g ( x , x 0 , ξ ) = f ( x 0 ) + ∑ k = 1 n a k ( x − x 0 ) k + f ( n + 1 ) ( ξ ) n ! ( x − x 0 ) n + 1 = f ( x 0 ) + ∑ k = 1 k = n f ( k ) ( x 0 ) k ! ( x − x 0 ) k + f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 \\ \def\taylor#1{ f(x)=g(x,#1,\xi)=f(x_0)+\sum\limits_{k=1}^{n} {a_k}(x-#1)^{k} \\+\frac{f^{(n+1)}(\xi)}{n!}{(x-#1)^{n+1}} } \taylor{x_0} \\=f(x_0)+\sum\limits_{k=1}^{k=n} {\frac{f^{(k)}{(x_0)}}{k!}}{(x-x_0)}^k +\frac{f^{(n+1)}(\xi)}{(n+1)!}{(x-x_0)^{n+1}} f(x)=g(x,x0,ξ)=f(x0)+k=1∑nak(x−x0)k+n!f(n+1)(ξ)(x−x0)n+1=f(x0)+k=1∑k=nk!f(k)(x0)(x−x0)k+(n+1)!f(n+1)(ξ)(x−x0)n+1
被 逼 近 函 数 = 逼 近 函 数 + 误 差 被 逼 近 函 数 可 以 用 逼 近 函 数 P n ( x , x 0 ) 来 估 计 误 差 可 以 用 R n ( x , x 0 ) 来 估 计 \\被逼近函数=逼近函数+误差 \\被逼近函数可以用逼近函数P_n(x,x_0)来估计 \\误差可以用R_n(x,x_0)来估计 被逼近函数=逼近函数+误差被逼近函数可以用逼近函数Pn(x,x0)来估计误差可以用Rn(x,x0)来估计
麦克劳林(Maclaurin)公式
当泰勒公式
令 x 0 = 0 ; f ( x ) = g ( x , 0 , ξ ) = f ( x 0 ) + ∑ k = 1 n a k ( x − 0 ) k + f ( n + 1 ) ( ξ ) n ! ( x − 0 ) n + 1 x 0 → ξ \def\taylor#1{ f(x)=g(x,#1,\xi)=f(x_0)+\sum\limits_{k=1}^{n} {a_k}(x-#1)^{k} \\+\frac{f^{(n+1)}(\xi)}{n!}{(x-#1)^{n+1}} } 令x_0=0; \\ \taylor{0} \\x_0\rightarrow \xi 令x0=0;f(x)=g(x,0,ξ)=f(x0)+k=1∑nak(x−0)k+n!f(n+1)(ξ)(x−0)n+1x0→ξ
其 中 : a k = f ( k ) ( x 0 ) k ! , x 0 = 0 ; a k x 0 = 0 = f ( k ) ( 0 ) k ! 其中:a_k=\frac{f^{(k)}{(x_0)}}{k!},x_0=0; \\ a_{k_{x_{0}=0}}=\frac{f^{(k)}(0)}{k!} 其中:ak=k!f(k)(x0),x0=0;akx0=0=k!f(k)(0)
即:
f ( x ) m a c l a u r i n = g ( x , 0 , ξ ) = f ( x 0 ) + ∑ k = 1 n f ( k ) ( 0 ) k ! x k + R n ( x ) 其 中 , R n ( x ) 可 以 是 l a g r a n g e 型 的 余 项 , 也 可 以 是 p e a n o 型 余 项 \underset{ {maclaurin}}{f(x)} =g(x,0,\xi) \\ =f{(x_0)}+\sum\limits_{k=1}^{n} {\frac{f^{(k)}(0)}{k!}}x^{k} +R_n(x) \\其中,R_{n}{(x)}可以是lagrange型的余项,也可以是peano型余项 maclaurinf(x)=g(x,0,ξ)=f(x0)+k=1∑nk!f(k)(0)xk+Rn(x)其中,Rn(x)可以是lagrange型的余项,也可以是peano型余项
在 m a c l a u r i n 公 式 下 , 取 R n ( x ) 为 l a g r a n g e 型 余 项 时 , 由 于 ξ ∈ ( x 0 , x ) , 可 以 令 ξ = θ x ; ( θ ∈ ( 0 , 1 ) ) 则 , R n ( x ) = f ( n + 1 ) ( θ x ) x n + 1 ( n + 1 ) ! 在maclaurin公式下,取R_{n}(x)为lagrange型余项时, \\由于\xi \in (x_0,x),可以令\xi=\theta x;(\theta \in (0,1)) \\则,R_{n}{(x)}=\frac{f^{(n+1)}(\theta x)x^{n+1}}{(n+1)!} 在maclaurin公式下,取Rn(x)为lagrange型余项时,由于ξ∈(x0,x),可以令ξ=θx;(θ∈(0,1))则,Rn(x)=(n+1)!f(n+1)(θx)xn+1
泰勒公式(麦克劳林公式)的应用
s i n ( x ) 带 有 l a r g r a n g e 型 余 项 的 n 阶 m a c l a u r i n 公 式 ( 展 开 ) sin(x)带有largrange型余项的n阶maclaurin公式(展开) sin(x)带有largrange型余项的n阶maclaurin公式(展开)
根据一般性的maclaurin公式:
f ( x ) m a c l a u r i n = f ( 0 ) + ∑ k = 1 k = n f ( k ) ( 0 ) k ! ⋅ x k + R n ( x ) R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ⋅ x ( n + 1 ) = f ( n + 1 ) ( θ x ) ( n + 1 ) ! ⋅ x ( n + 1 ) \underset{maclaurin}{f(x)} =f(0)+\sum_{k=1}^{k=n} {\frac{f^{(k)}(0)}{k!}} \cdot{x^k}+R_n{(x)} \\ R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}\cdot x^{(n+1)} =\frac{f^{(n+1)}(\theta x)}{(n+1)!}\cdot x^{(n+1)} maclaurinf(x)=f(0)+k=1∑k=nk!f(k)(0)⋅xk+Rn(x)Rn(x)=(n+1)!f(n+1)(ξ)⋅x(n+1)=(n+1)!f(n+1)(θx)⋅x(n+1)
f ( k ) ( x ) = s i n ( x + k ⋅ π 2 ) f ( k ) ( 0 ) = s i n ( k π 2 ) ; ( k = 1 , 2 , 3 , ⋯ ) = 1 , 0 , − 1 , 0 , 1 , 0 , ⋯ ( 根 据 单 位 圆 , 不 难 发 现 其 周 期 规 律 ) f ( 0 ) = s i n ( 0 ) = 0 f ( x ) = x − x 3 3 ! + x 5 5 ! + ⋯ f^{(k)}(x)=sin(x+k\cdot \frac{\pi}{2}) \\ f^{(k)}(0)=sin(k\frac{\pi}{2});(k=1,2,3,\cdots) \\=1,0,-1,0,1,0,\cdots(根据单位圆,不难发现其周期规律) \\f(0)=sin(0)=0 \\f(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots f(k)(x)=sin(x+k⋅2π)f(k)(0)=sin(k2π);(k=1,2,3,⋯)=1,0,−1,0,1,0,⋯(根据单位圆,不难发现其周期规律)f(0)=sin(0)=0f(x)=x−3!x3+5!x5+⋯
k 1 2 3 4 5 6 … n=2m f ( k ) ( 0 ) f^{(k)}(0) f(k)(0) 1 0 -1 0 1 0 f ( k ) ( 0 ) k ! \frac{f^{(k)}(0)}{k!} k!f(k)(0) 1 1 ! \frac{1}{1!} 1!1 0 2 ! = 0 \frac{0}{2!}=0 2!0=0 − 1 3 ! \frac{-1}{3!} 3!−1 0 4 ! = 0 \frac{0}{4!}=0 4!0=0 1 5 ! \frac{1}{5!} 5!1 0 6 ! \frac{0}{6!} 6!0 f ( k ) ( 0 ) k ! x k \frac{f^{(k)}(0)}{k!}x^k k!f(k)(0)xk x 1 x^1 x1 0 − 1 3 ! x 3 -\frac{1}{3!}x^3 −3!1x3 0 + 1 5 ! x 5 +\frac{1}{5!}x^5 +5!1x5 0 第m项 1 2 3 4 5 6 … m (m+1)余项 2m 2 4 6 8 10 12 m-1 0 1 2 3 4 5 2m-1 1 3 5 7 9 11 2m+1 3 5 7 9 11 13 ( − 1 ) m − 1 (-1)^{m-1} (−1)m−1(作为项的符号) 1 -1 1 -1 1 -1 ( − 1 ) m − 1 (-1)^{m-1} (−1)m−1 ( − 1 ) m (-1)^{m} (−1)m ( − 1 ) m (-1)^{m} (−1)m -1 1 -1 1 -1 1 f ( k ) ( 0 ) k ! x k \frac{f^{(k)}(0)}{k!}x^k k!f(k)(0)xk x 1 x^1 x1 0 − 1 3 ! x 3 -\frac{1}{3!}x^3 −3!1x3 0 + 1 5 ! x 5 +\frac{1}{5!}x^5 +5!1x5 0 ( − 1 ) m − 1 x 2 m − 1 ( 2 m − 1 ) ! (-1)^{m-1}\frac{x^{2m-1}}{(2m-1)!} (−1)m−1(2m−1)!x2m−1 ( − 1 ) m c o s ( θ x ) ( 2 m + 1 ) ! x 2 m + 1 (-1)^m\frac{cos(\theta x)}{(2m+1)!}x^{2m+1} (−1)m(2m+1)!cos(θx)x2m+1 f ( x ) = x − x 3 3 ! + x 5 5 ! − ⋯ + ( − 1 ) ( m − 1 ) x 2 m − 1 ( 2 m − 1 ) ! + R 2 m f ( x ) = ∑ k = 1 k = m ( − 1 ) ( m − 1 ) x 2 m − 1 ( 2 m − 1 ) ! + R 2 m R 2 m ( x ) = s i n ( θ x + ( 2 m + 1 ) π 2 ) ( 2 m + 1 ) ! x ( 2 m + 1 ) = ( − 1 ) m c o s ( θ x ) ( 2 m + 1 ) ! x 2 m + 1 f(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots+(-1)^{(m-1)}\frac{x^{2m-1}}{(2m-1)!}+R_{2m} \\ f(x)=\sum_{k=1}^{k=m} (-1)^{(m-1)} {\frac{x^{2m-1}}{(2m-1)!}}+R_{2m} \\R_{2m}(x)=\frac{sin(\theta x+(2m+1)\frac{\pi}{2})}{(2m+1)!}x^{(2m+1)} =(-1)^m\frac{cos(\theta x)}{(2m+1)!}x^{2m+1} f(x)=x−3!x3+5!x5−⋯+(−1)(m−1)(2m−1)!x2m−1+R2mf(x)=k=1∑k=m(−1)(m−1)(2m−1)!x2m−1+R2mR2m(x)=(2m+1)!sin(θx+(2m+1)2π)x(2m+1)=(−1)m(2m+1)!cos(θx)x2m+1
如果取m=1;得到
s i n x ≈ x sinx\approx x sinx≈x此 时 用 P ( x ) = x 估 算 f ( x ) = s i n ( x ) 产 生 的 误 差 为 此时用P(x)=x估算f(x)=sin(x)产生的误差为 此时用P(x)=x估算f(x)=sin(x)产生的误差为:
∣ R 2 ∣ = ∣ − c o s ( θ x ) 3 ! x 3 ∣ ⩽ ∣ x 3 ∣ 6 |R_2|=|-\frac{cos(\theta x)}{3!}x^3|\leqslant\frac{|x^3|}{6} ∣R2∣=∣−3!cos(θx)x3∣⩽6∣x3∣可见,当要估算的f(x),x取值较小的时候,使用P(x)=x估算f(x)=sin(x)差生的误差很有限
当x取值较大时,误差上限会变大,估算效果可能很不靠谱,这时,可以考虑使用高阶的逼近函数
m=2;得到
s i n x ≈ x − 1 3 ! x 3 sinx\approx x-\frac{1}{3!}x^3 sinx≈x−3!1x3m=3;得到
s i n x ≈ x − 1 3 ! x 3 + 1 5 ! x 5 sinx\approx x-\frac{1}{3!}x^3+\frac{1}{5!}x^5 sinx≈x−3!1x3+5!1x5
他们产生的误差不会分别不会超过 1 5 ! ∣ x 5 ∣ , 1 7 ! x 7 \frac{1}{5!}|x^5|,\frac{1}{7!}x^7 5!1∣x5∣,7!1x7;而阶乘增长的比指数要快,因此可以相信高阶逼近可以更好的控制误差在足够小的范围内
泰勒展开的应用 ( x 0 ≠ 0 ) (x_0\neq 0) (x0=0)
f ( x ) = f ( x 0 ) + ∑ k = 1 k = n f ( k ) ( x 0 ) k ! ( x − x 0 ) k + R n ( x ) f(x) =f(x_0)+\sum\limits_{k=1}^{k=n} {\frac{f^{(k)}{(x_0)}}{k!}}{(x-x_0)}^k +R_n(x) f(x)=f(x0)+k=1∑k=nk!f(k)(x0)(x−x0)k+Rn(x)
f ( x ) = x 3 + 3 x 2 − 2 x + 4 的 按 ( x + 1 ) 的 升 幂 展 开 f(x)=x^3+3x^2-2x+4的按(x+1)的升幂展开 f(x)=x3+3x2−2x+4的按(x+1)的升幂展开
- 确 定 x 0 = − 1 确定x_0=-1 确定x0=−1
- 计算f(x)在各阶导数,并带入 x = x 0 , 得 到 f ( k ) ( x 0 ) x=x_0,得到f^{(k)}(x_0) x=x0,得到f(k)(x0)
- 计算 R n ( x ) R_n(x) Rn(x)
- 带入公式
x 0 = − 1 ; f ( − 1 ) = 8 ; f ( x ) 在 x = x 0 = − 1 处 的 各 阶 导 数 值 : f ′ ( x ) = 3 x 2 + 6 x − 2 ; f ′ ( − 1 ) = − 5 f ′ ′ ( x ) = 6 x + 6 ; f ′ ′ ( − 1 ) = 0 f ′ ′ ′ ( x ) = 6 ; f ′ ′ ′ ( − 1 ) = 6 f ( k ) ( x ) = 0 ; ( k ⩾ 4 ) 所 以 R = R 4 ( x ) = 0 ∴ f ( x ) = f ( − 1 ) + f ′ ( − 1 ) 1 ! ( x + 1 ) + f ′ ′ ( − 1 ) 2 ! ( x + 1 ) + f ′ ′ ′ ( − 1 ) 3 ! x + 1 + R 4 ( x ) = 8 − 5 ( x + 1 ) + ( x + 1 ) 3 x_0=-1; \\ f(-1)=8; \\f(x)在x=x_0=-1处的各阶导数值: f'(x)=3x^2+6x-2;f'(-1)=-5 \\f''(x)=6x+6;f''(-1)=0 \\f'''(x)=6;f'''(-1)=6 \\f^{(k)}{(x)}=0;(k\geqslant 4) 所以R=R_4(x)=0 \\ \therefore f(x)=f(-1)+\frac{f'(-1)}{1!}(x+1)+\frac{f''(-1)}{2!}(x+1)+\frac{f'''(-1)}{3!}{x+1}+R_4(x) \\=8-5(x+1)+(x+1)^3 x0=−1;f(−1)=8;f(x)在x=x0=−1处的各阶导数值:f′(x)=3x2+6x−2;f′(−1)=−5f′′(x)=6x+6;f′′(−1)=0f′′′(x)=6;f′′′(−1)=6f(k)(x)=0;(k⩾4)所以R=R4(x)=0∴f(x)=f(−1)+1!f′(−1)(x+1)+2!f′′(−1)(x+1)+3!f′′′(−1)x+1+R4(x)=8−5(x+1)+(x+1)3
边栏推荐
- A green plug-in that allows you to stay focused, live and work hard
- 變化是永恒的主題
- leetcode:11. Container with the most water [double pointer + greed + remove the shortest board]
- Failed to start component [StandardEngine[Catalina]. StandardHost[localhost]. StandardContext
- SQL: special update operation
- JS_ Array_ sort
- Multifunctional web file manager filestash
- 平淡的生活里除了有扎破皮肤的刺,还有那些原本让你魂牵梦绕的诗与远方
- 189. Rotation array
- High concurrency Architecture - read write separation
猜你喜欢
![235. The nearest common ancestor of the binary search tree [LCA template + same search path]](/img/f5/f2d244e7f19e9ddeebf070a1d06dce.png)
235. The nearest common ancestor of the binary search tree [LCA template + same search path]

SSM整合-前后台协议联调(列表功能、添加功能、添加功能状态处理、修改功能、删除功能)
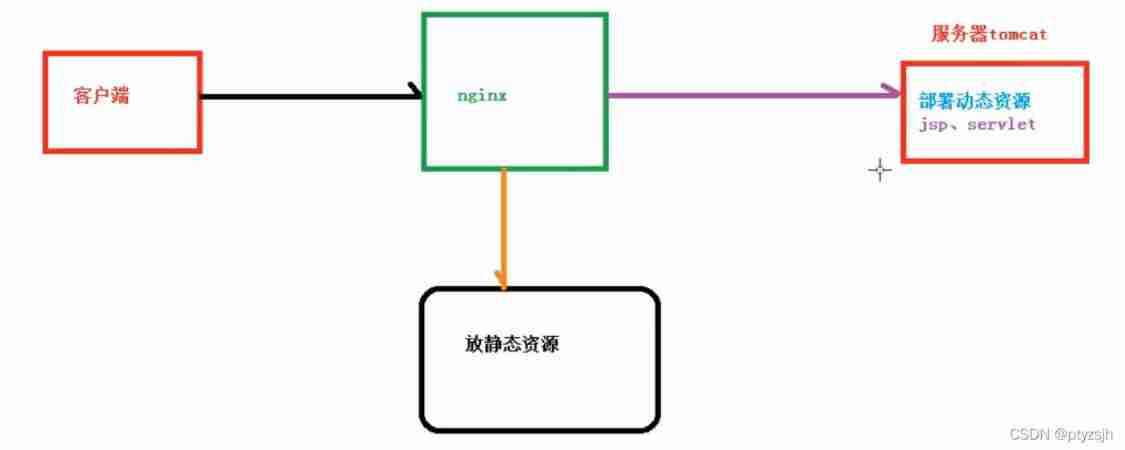
4. Load balancing and dynamic static separation
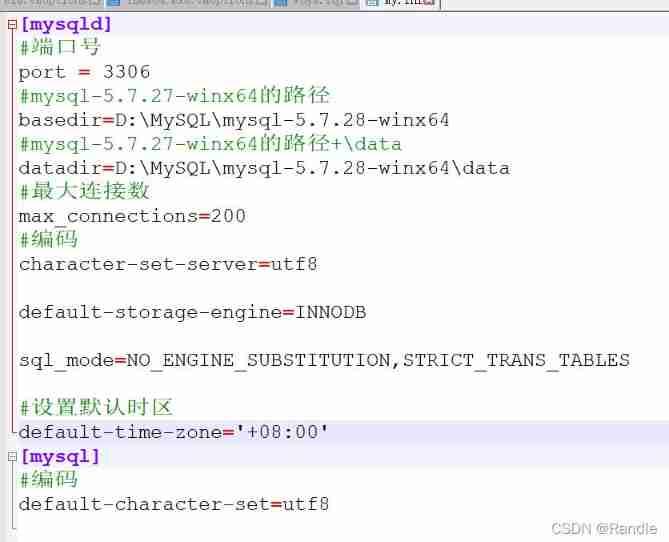
Record: MySQL changes the time zone

235. 二叉搜索树的最近公共祖先【lca模板 + 找路径相同】

NFT新的契机,多媒体NFT聚合平台OKALEIDO即将上线
![[leetcode周赛]第300场——6110. 网格图中递增路径的数目-较难](/img/8d/0e515af6c17971ddf461e3f3b87c30.png)
[leetcode周赛]第300场——6110. 网格图中递增路径的数目-较难

Help change the socket position of PCB part
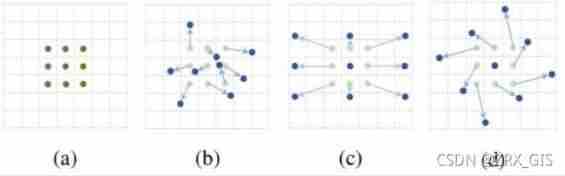
How many convolution methods does deep learning have? (including drawings)

KINGS
随机推荐
Max of PHP FPM_ Some misunderstandings of children
Day-27 database
Common PostgreSQL commands
TypeScript 官网教程
组策略中开机脚本与登录脚本所使用的用户身份
235. The nearest common ancestor of the binary search tree [LCA template + same search path]
PyTorch中在反向传播前为什么要手动将梯度清零?
“google is not defined” when using Google Maps V3 in Firefox remotely
User identity used by startup script and login script in group policy
The online customer service system developed by PHP is fully open source without encryption, and supports wechat customer service docking
SSH 远程执行命令简介
Boost. Asio Library
Caddy server agent
4. Load balancing and dynamic static separation
Transformer T5 model read slowly
Mysql45 lecture learning notes (II)
Succession of flutter
Find the median of two positive arrays
Torch learning notes (3) -- univariate linear regression model (self training)
Recommend a simple browser tab