当前位置:网站首页>Summary of leetcode's dynamic programming 4
Summary of leetcode's dynamic programming 4
2022-07-06 06:25:00 【nuist__ NJUPT】
leetcode Summary of dynamic programming 4
1- The longest palindrome subsequence
Topic link : The title link is here !!!
Ideas : Dynamic programming
dp[i][j]: Indicates from subscript i To the subscript j Maximum palindrome sequence of
if s[i]==s[j]
The recurrence formula is as follows :
dp[i][j] = dp[i+1][j-1]+2 ;
if s[i]!=s[j]
The recurrence formula is as follows :
dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]) ;
class Solution {
public int longestPalindromeSubseq(String s) {
int n = s.length() ;
int [][] dp = new int [n][n] ;
for(int i=0; i<n; i++){
dp[i][i] = 1 ;
}
for(int i=n-1; i>=0; i--){
for(int j=i+1; j<n; j++){
if(s.charAt(i) != s.charAt(j)){
dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]) ;
}else{
dp[i][j] = dp[i+1][j-1]+2 ;
}
}
}
return dp[0][n-1] ;
}
}
2- One and zero
Topic link : The title link is here !!!
Ideas : Deformation of knapsack problem
This problem is very similar to the classic knapsack problem , But there is only one capacity different from the classical knapsack problem , This problem has two capacities , That is... In the selected string subset 0 and 1 The maximum number of .
The classical knapsack problem can be solved by two-dimensional dynamic programming , The two dimensions are goods and capacity . This problem has two capacities , Therefore, it is necessary to use three-dimensional dynamic programming to solve , The three dimensions are string 、0 Capacity and 1 The capacity of .
Define 3D array dp, among dp[i][j][k] In front of i In strings , Use j individual 0 and k individual 1 The maximum number of strings that can be obtained in the case of .
The equation of state transfer is as follows :
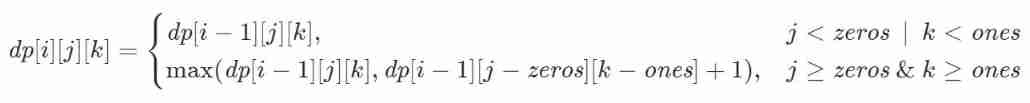
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int len = strs.length ;
int [][][] dp = new int [len+1][m+1][n+1] ;
for(int i=1; i<=len; i++){
int [] zero =count(strs[i-1]) ;
int zeros = zero[0], ones = zero[1] ;
for(int j=0; j<=m; j++){
for(int k=0; k<=n; k++){
if(j>=zeros && k>=ones){
dp[i][j][k] = Math.max(dp[i-1][j][k],dp[i-1][j-zeros][k-ones]+1) ;
}else{
dp[i][j][k] = dp[i-1][j][k] ;
}
}
}
}
return dp[len][m][n] ;
}
public int [] count(String s){
int [] zeros = new int [2] ;
for(int i=0; i<s.length(); i++){
zeros[s.charAt(i)-'0']++ ;
}
return zeros ;
}
}
3- Use the minimum cost to climb the stairs
Topic link : The title link is here !!!
Ideas :dp[i]: Means to climb to the current i The minimum cost of location
dp[0]=0
dp[1]=0
Recursive expression :
dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]) ;
class Solution {
public int minCostClimbingStairs(int[] cost) {
int [] dp = new int [cost.length+1] ;
for(int i=2; i<=cost.length; i++){
dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]) ;
}
return dp[cost.length];
}
}
4- Change for II
Topic link : The title link is here !!!
Ideas : use dp[x] Indicates that the sum of the amounts equals x Number of coin combinations , The goal is to seek dp[amount]. The boundary of dynamic programming is dp[0]=1. Only when no coin is selected , The sum of the amount is 0, So only 1 A combination of coins .
class Solution {
public int change(int amount, int[] coins) {
int [] dp = new int [amount+1] ;
dp[0] = 1 ;
for(int coin : coins){
for(int i=coin; i<=amount; i++){
dp[i] += dp[i-coin] ;
}
}
return dp[amount] ;
}
}
5- A beautiful arrangement
Topic link : The title link is here !!!
Ideas 1:dfs+ Mark
Every round of search , As long as the current number and subscript can be taken from each other , Then accumulate the permutation number , Continue to search . Each search needs to mark the number that has been searched .
class Solution {
public int countArrangement(int n) {
return dfs(n,1,new boolean[n+1]) ;
}
public int dfs(int n, int i, boolean [] vis){
if(i>n){
return 1 ;
}
int ans = 0 ;
for(int num=1; num<=n; num++){
if(!vis[num] &&(i%num==0 || num%i==0)){
vis[num] = true ;
ans += dfs(n,i+1,vis) ;
vis[num] = false ;
}
}
return ans ;
}
}
Ideas 2: backtracking
We can use backtracking to solve this problem , Put the number into the target arrangement from left to right .
In particular , We define functions backtrack(i,n), Indicates an attempt to move to the location i Put in number . among n Indicates the length of the arrangement . In the current function , We first find a qualified unused number , Then recursively backtrack(i+1,n), When the function is finished , Go back to the current layer , Let's try the next qualified unused number .
Back in the process , We can use vis Array marks which numbers have been used , Every time we choose a number idx, We will vis[idx] Marked as true, When backtracking is complete , Let's set it to false.
Specially , To optimize backtracking efficiency , We can preprocess the number of qualified for each location , Using arrays match preservation . When we try to position i When you put in the number , We just need to traverse match[i] that will do .
class Solution {
List<Integer> [] match ;
boolean [] vis ;
int num ;
public int countArrangement(int n) {
match = new List[n+1] ;
vis = new boolean[n+1] ;
for(int i=1; i<=n; i++){
match[i] = new ArrayList<>() ;
}
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(i%j==0 || j%i==0){
match[i].add(j) ;
}
}
}
backtrack(1,n) ;
return num ;
}
public void backtrack(int i, int n){
if(i==n+1){
num++ ;
return ;
}
for(int idx : match[i]){
if(!vis[idx]){
vis[idx] = true ;
backtrack(i+1,n) ;
vis[idx] = false ;
}
}
}
}
6- The number of paths out of bounds
Topic link : The title link is here !!!
Ideas : Search for + Mark
Search in four directions in each round , If you can get out of bounds, you will accumulate 1, The steps are 0 when , Can't go out of bounds , return 0, After the search is completed, you need to mark the answers that have been searched in the current position under a certain number of steps , When the next round of search encounters , Just go back .
class Solution {
int [] dx = {
-1,1,0,0} ;
int [] dy = {
0,0,-1,1} ;
int [][][]cache ;
int mod = 1000000007;
public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
cache = new int [m][n][maxMove+1] ;
for(int i=0; i<m; i++){
for(int j=0; j<n; j++){
for(int k=1; k<=maxMove; k++){
cache[i][j][k] = -1 ;
}
}
}
return dfs(startRow,startColumn,maxMove,m,n) ;
}
public int dfs(int x, int y, int maxMove, int m, int n){
if(x<0 || y<0 || x>=m || y>=n){
return 1 ;
}
if(maxMove==0){
return 0 ;
}
if(cache[x][y][maxMove]!=-1){
return cache[x][y][maxMove] ;
}
int ans = 0 ;
for(int i=0; i<4; i++){
int tx = x + dx[i] ;
int ty = y + dy[i] ;
ans += dfs(tx,ty,maxMove-1,m,n) ;
ans = ans % mod ;
}
cache[x][y][maxMove] = ans ;
return ans ;
}
}
Ideas : Dynamic programming
The state of dynamic planning is determined by the number of moves 、 Rows and columns determine , Definition dp[i][j][k] Indicates that the ball moves i After times, it is located in the coordinate (j,k) Number of paths for .
class Solution {
int [] dx = {
-1,1,0,0} ;
int [] dy = {
0,0,-1,1} ;
int mod = 1000000007 ;
public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
int [][][] dp = new int [maxMove+1][m][n] ;
dp[0][startRow][startColumn] = 1;
int sum = 0 ;
for(int i=0; i<maxMove; i++){
for(int j=0; j<m; j++){
for(int k=0; k<n; k++){
int count = dp[i][j][k] ;
if(count > 0){
for(int x=0; x<4; x++){
int tx = j + dx[x] ;
int ty = k + dy[x] ;
if(tx>=0 && tx<m && ty>=0 && ty<n){
dp[i+1][tx][ty] = (dp[i+1][tx][ty]+count) % mod ;
}else{
sum = (sum+count)%mod ;
}
}
}
}
}
}
return sum ;
}
}
7- Deletion of two strings
Topic link : The title link is here !!!
Ideas :dp[i][j] Said to i-1 String word1, With j-1 a null-terminated string word2 To achieve equality , The minimum number of elements to delete .
if word1[i-1] be equal to word2[j-1] You don't need to delete , The recurrence formula is as follows :
dp[i][j] = dp[i-1][j-1] ;
if word1[i-1] It's not equal to word2[j-1], You need to delete , There are three possibilities , The recurrence formula is as follows :
dp[i][j] = Math.min(dp[i-1][j]+1,Math.min(dp[i][j-1]+1,dp[i-1][j-1]+2)) ;
class Solution {
public int minDistance(String word1, String word2) {
int [][] dp = new int [word1.length()+1][word2.length()+1] ;
for(int i=1; i<word1.length()+1; i++){
dp[i][0] = i ;
}
for(int j=1; j<word2.length()+1; j++){
dp[0][j] = j ;
}
for(int i=1; i<word1.length()+1; i++){
for(int j=1; j<word2.length()+1; j++){
if(word1.charAt(i-1)==word2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1] ;
}else{
dp[i][j] = Math.min(dp[i-1][j]+1,Math.min(dp[i][j-1]+1,dp[i-1][j-1]+2)) ;
}
}
}
return dp[word1.length()][word2.length()] ;
}
}
8- Palindrome string
Topic link : The title link is here !!!
Ideas :dp[j][i] From position j To the position i Is it a palindrome string .
If s.charAt(i)==s.charAt(j)
And (i-j<2 || dp[j+1][i-1])
It must be a palindrome string .
class Solution {
public int countSubstrings(String s) {
boolean [][] dp = new boolean [s.length()][s.length()] ;
int cnt = 0 ;
for(int i=0; i<s.length(); i++){
for(int j=0; j<=i; j++){
if(s.charAt(i)==s.charAt(j)&&(i-j<2 || dp[j+1][i-1])){
dp[j][i] = true ;
cnt ++ ;
}
}
}
return cnt ;
}
}
9- The number of longest increasing subsequences
Topic link : The title link is here !!!
determine dp The meaning of arrays and subscripts
For this topic, we will maintain two arrays together .
dp[i]:i Before ( Include i) The length of the longest increasing subsequence is dp[i]
cnt[i]: With nums[i] String ending with , The number of longest increasing subsequences is cnt[i]
Determine the recurrence formula
In the longest ascending subsequence , The state transition we give is :
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
namely : Location i The longest increasing subsequence length of be equal to j from 0 To i-1 The longest ascending subsequence at each position + 1 The maximum of .
This question is not so simple , We need to consider two dimensions , One is dp[i] Update , One is cnt[i] Update .
So how to update cnt[i] Well ?
With nums[i] String ending with , The number of longest increasing subsequences is cnt[i].
So in nums[i] > nums[j] On the premise of , If in [0, i-1] Within the scope of , eureka j, bring dp[j] + 1 > dp[i], It indicates that a longer increasing subsequence has been found .
So in order to j Increment the number of subsequences for the longest substring at the end , Is the latest in i Increment the number of subsequences for the longest substring at the end , namely :cnt[i] = cnt[j].
stay nums[i] > nums[j] On the premise of , If in [0, i-1] Within the scope of , eureka j, bring dp[j] + 1 == dp[i], It shows that two increasing subsequences of the same length are found .
So in order to i Increment the number of subsequences for the longest substring at the end You should add j Increment the number of subsequences for the longest substring at the end , namely :cnt[i] += cnt[j];
class Solution {
public int findNumberOfLIS(int[] nums) {
if(nums.length<=1){
return nums.length ;
}
int [] dp = new int [nums.length] ;
int [] cnt = new int [nums.length] ;
Arrays.fill(dp,1) ;
Arrays.fill(cnt,1) ;
int max = 0 ;
for(int i=1; i<nums.length; i++){
for(int j=0; j<i; j++){
if(nums[i]>nums[j]){
if(dp[j]+1 > dp[i]){
dp[i] = dp[j]+1 ;
cnt[i] = cnt[j] ;
}else if(dp[j]+1==dp[i]){
cnt[i] += cnt[j] ;
}
}
}
max = Math.max(max, dp[i]) ;
}
int ans = 0 ;
for(int i=0; i<dp.length; i++){
if(max==dp[i]){
ans += cnt[i] ;
}
}
return ans ;
}
}
10- A keyboard with only two keys
Topic link : The title link is here !!!
Ideas :1、 If n Is a prime number , So the result is n, Because the least is to copy , Then paste one by one .
2、 If n Is a composite number , Then his result is the sum of the results of the factorization .
such as n by 8 ,
that dp[8] = dp[4]+dp[2]; because ,8 = 42
dp[4] = dp[2]+dp[2]; because ,4 = 22
Because because 2 It's a prime number ,dp[2] = 2;
therefore dp[8] = 6 That's what we're asking for .
class Solution {
public int minSteps(int n) {
int [] dp = new int [n+1] ;
for(int i=2; i<=n; i++){
dp[i] = i ;
for(int j=2;j<=Math.sqrt(i);j++){
if(i%j==0){
dp[i] = dp[j] + dp[i/j] ;
break ;
}
}
}
return dp[n];
}
}
A journey of a thousand miles begins with a single step. , take your time , It will be soon !!!
边栏推荐
- 模拟卷Leetcode【普通】1109. 航班预订统计
- 生物医学英文合同翻译,关于词汇翻译的特点
- 国际经贸合同翻译 中译英怎样效果好
- LeetCode 1200. 最小绝对差
- University of Manchester | dda3c: collaborative distributed deep reinforcement learning in swarm agent systems
- [Tera term] black cat takes you to learn TTL script -- serial port automation skill in embedded development
- G - Supermarket
- Simulation volume leetcode [general] 1219 Golden Miner
- 模拟卷Leetcode【普通】1219. 黄金矿工
- Qt:无法定位程序输入点XXXXX于动态链接库。
猜你喜欢
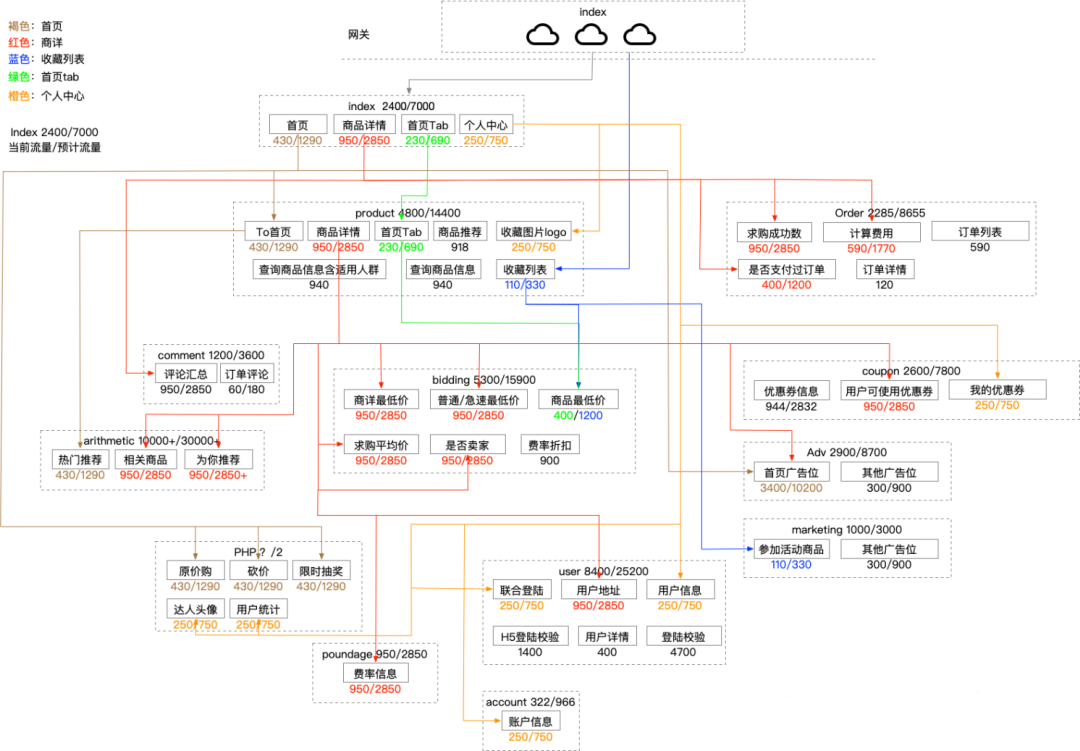
Full link voltage measurement: building three models
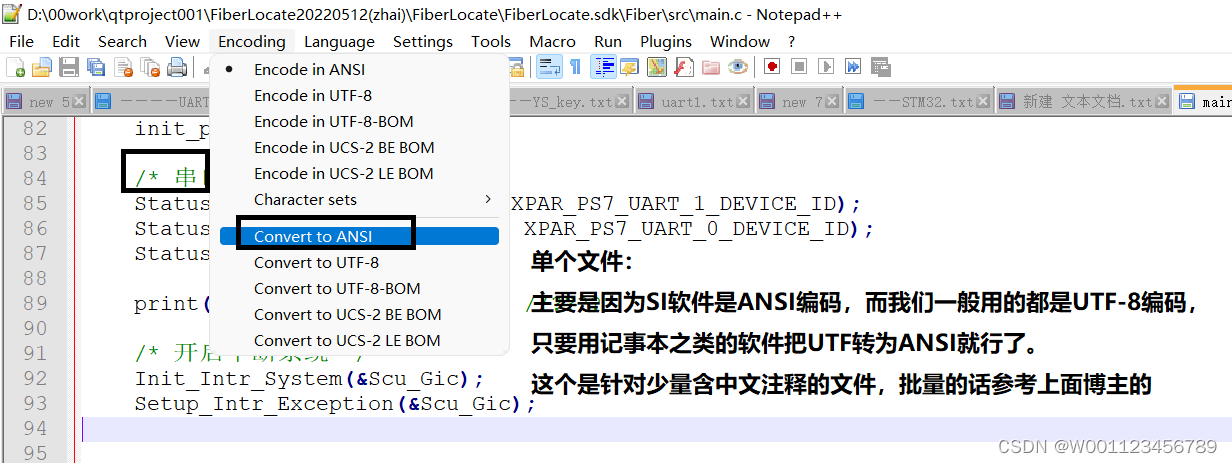
sourceInsight中文乱码

How to extract login cookies when JMeter performs interface testing
記一個基於JEECG-BOOT的比較複雜的增删改功能的實現

Manage configuration using Nacos
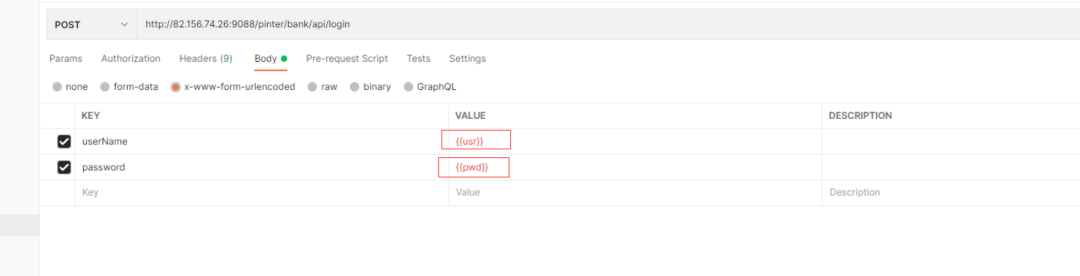
Postman core function analysis - parameterization and test report
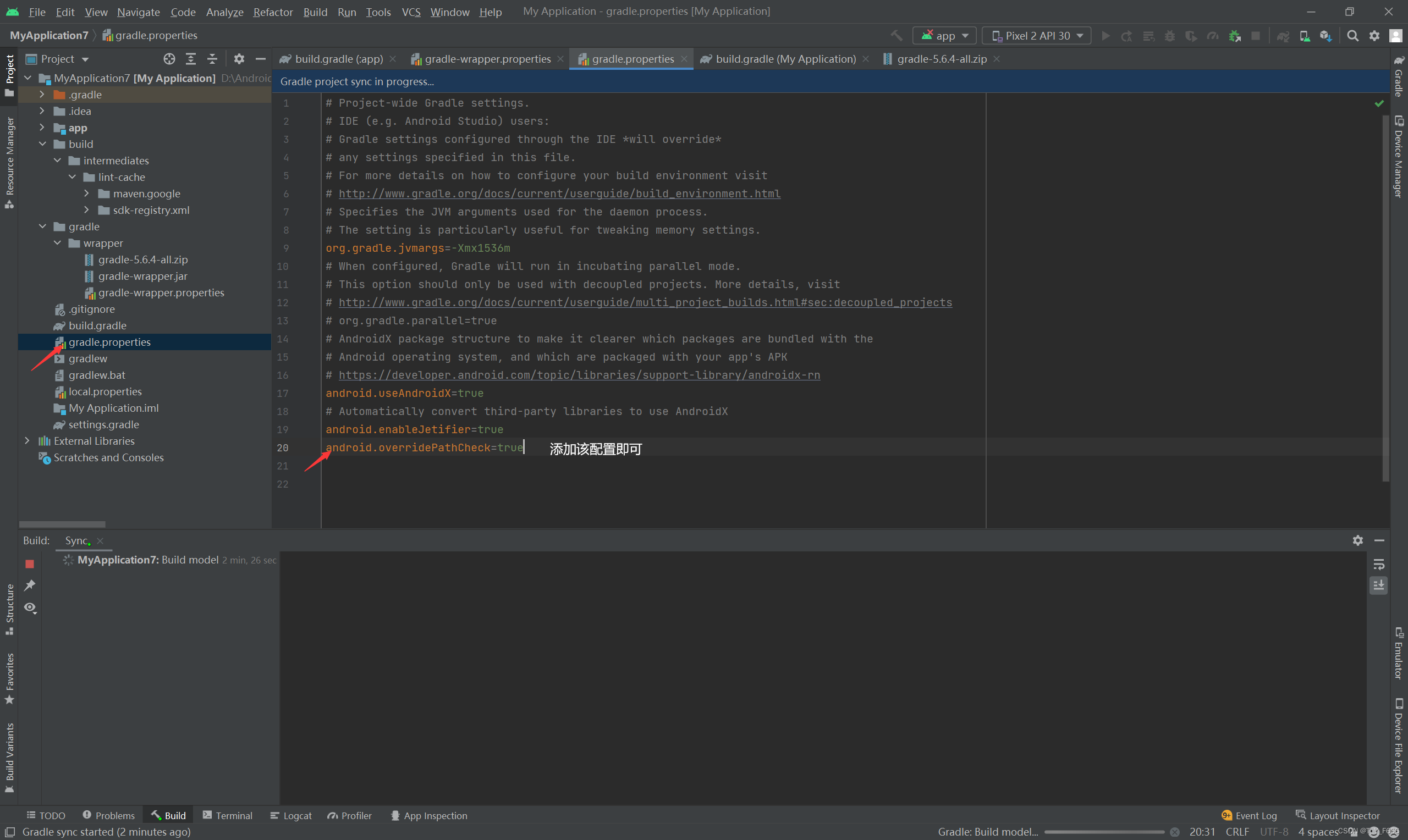
Caused by:org. gradle. api. internal. plugins . PluginApplicationException: Failed to apply plugin

Drug disease association prediction based on multi-scale heterogeneous network topology information and multiple attributes
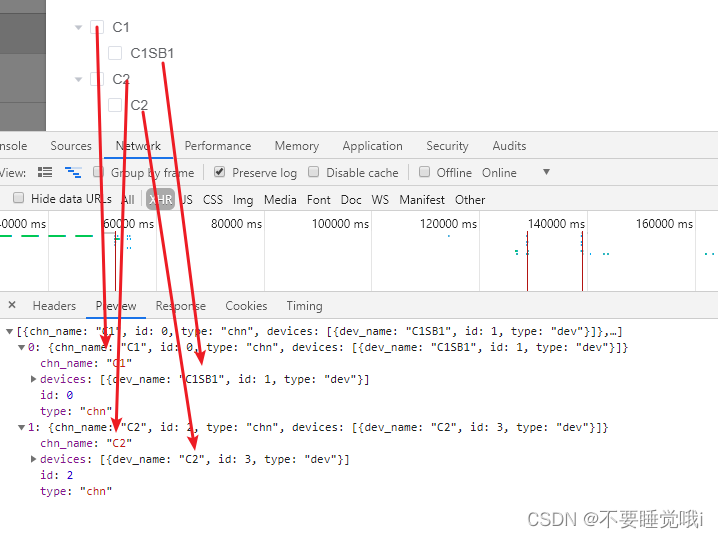
把el-tree选中的数组转换为数组对象

【Tera Term】黑猫带你学TTL脚本——嵌入式开发中串口自动化神技能
随机推荐
Redis 核心技术与实战之 基本架构:一个键值数据库包含什么?
Still worrying about how to write web automation test cases? Senior test engineers teach you selenium test case writing hand in hand
Simulation volume leetcode [general] 1091 The shortest path in binary matrix
把el-tree选中的数组转换为数组对象
Caused by:org. gradle. api. internal. plugins . PluginApplicationException: Failed to apply plugin
Summary of anomaly detection methods
MFC on the conversion and display of long string unsigned char and CString
Black cat takes you to learn UFS Protocol Part 8: UFS initialization (boot operation)
【MQTT从入门到提高系列 | 01】从0到1快速搭建MQTT测试环境
Py06 字典 映射 字典嵌套 键不存在测试 键排序
D - How Many Answers Are Wrong
如何将flv文件转为mp4文件?一个简单的解决办法
技术分享 | 常见接口协议解析
Simulation volume leetcode [general] 1143 Longest common subsequence
使用Nacos管理配置
[postman] collections - run the imported data file of the configuration
[C language] string left rotation
模拟卷Leetcode【普通】1314. 矩阵区域和
LeetCode 1200. 最小绝对差
Transfert des paramètres de la barre d'adresse de la page de liste basée sur jeecg - boot