Link to the original text ： http://tecdat.cn/?p=3385
The source of the original text is ： The official account of the tribal public
Recently I was asked to write about financial time series copulas The investigation of . Get descriptions of various models from the read data , It includes some graphical and statistical output .
> oil = read.xlsx（temp,sheetName =“DATA”,dec =“,”）Then we can plot these three time series
1 1997-01-10 2.73672 2.25465 3.3673 1.5400
2 1997-01-17 -3.40326 -6.01433 -3.8249 -4.1076
3 1997-01-24 -4.09531 -1.43076 -6.6375 -4.6166
4 1997-01-31 -0.65789 0.34873 0.7326 -1.5122
5 1997-02-07 -3.14293 -1.97765 -0.7326 -1.8798
6 1997-02-14 -5.60321 -7.84534 -7.6372 -11.0549
The idea is to use some variables here ARMA-GARCH The process . The heuristic here is the first part used to simulate the dynamics of time series averages , The second part is used to simulate the dynamic variance of time series .
Two models are considered in this paper
- About ARMA Multivariable model residuals GARCH The process （ Or variance matrix dynamics model ）
- About ARMA-GARCH Multivariate models of process residuals （ be based on copula）
therefore , Here we will consider different sequences , As residuals of different models . We can also standardize these residuals .
ARMA Model
> fit1 = arima（x = dat \[,1\],order = c（2,0,1））
> fit2 = arima（x = dat \[,2\],order = c（1,0,1））
> fit3 = arima（x = dat \[,3\],order = c（1,0,1））
> m < - apply（dat_arma,2,mean）
> v < - apply（dat_arma,2,var）
> dat\_arma\_std < - t（（t（dat_arma）-m）/ sqrt（v））ARMA-GARCH Model
> fit1 = garchFit（formula = ~arma（2,1）+ garch（1,1）,data = dat \[,1\],cond.dist =“std”）
> fit2 = garchFit（formula = ~arma（1,1）+ garch（1,1）,data = dat \[,2\],cond.dist =“std”）
> fit3 = garchFit（formula = ~arma（1,1）+ garch（1,1）,data = dat \[,3\],cond.dist =“std”）
> m\_res < - apply（dat\_res,2,mean）
> v\_res < - apply（dat\_res,2,var）
> dat\_res\_std = cbind（（dat\_res \[,1\] -m\_res \[1\]）/ sqrt（v\_res \[1\]）,（dat\_res \[,2\] -m\_res \[2\]）/ sqrt（v\_res \[2\]）,（dat\_res \[ ,3\] -m\_res \[3\]）/ SQRT（v_res \[3\]））Multivariable GARCH Model
The first model to consider is Covariance matrix Of Multivariable EWMA,
> ewma = EWMAvol（dat\_res\_std,lambda = 0.96）Volatility
> emwa\_series\_vol = function（i = 1）{
+ lines（Time,dat_arma \[,i\] + 40,col =“gray”）
+ j = 1
+ if（i == 2）j = 5
+ if（i == 3）j = 9
Implied relevance
> emwa\_series\_cor = function（i = 1,j = 2）{
+ if（（min（i,j）== 1）＆（max（i,j）== 2））{
+ a = 1; B = 9; AB = 3}
+ r = ewma $ Sigma.t \[,ab\] / sqrt（ewma $ Sigma.t \[,a\] *
+ ewma $ Sigma.t \[,b\]）
+ plot（Time,r,type =“l”,ylim = c（0,1））
+}
Multivariable GARCH, namely BEKK（1,1） Model , For example, using ：
> bekk = BEKK11（dat_arma）
> bekk\_series\_vol function（i = 1）{
+ plot（Time, $ Sigma.t \[,1\],type =“l”,
+ ylab = （dat）\[i\],col =“white”,ylim = c（0,80））
+ lines（Time,dat_arma \[,i\] + 40,col =“gray”）
+ j = 1
+ if（i == 2）j = 5
+ if（i == 3）j = 9
> bekk\_series\_cor = function（i = 1,j = 2）{
+ a = 1; B = 5; AB = 2}
+ a = 1; B = 9; AB = 3}
+ a = 5; B = 9; AB = 6}
+ r = bk $ Sigma.t \[,ab\] / sqrt（bk $ Sigma.t \[,a\] *
+ bk $ Sigma.t \[,b\]）
From a single variable GARCH The simulated residuals in the model
The first step may be to consider some of the static residuals （ union ） Distribution . The univariate marginal distribution is
Edge density contour （ Obtained using a bivariate kernel estimator ）
Can also be copula Density Visualization （ There are some nonparametric estimates , Here are the parameters copula）
> copula_NP = function（i = 1,j = 2）{
+ n = nrow（uv）
+ s = 0.3
+ norm.cop < - normalCopula（0.5）
+ norm.cop < - normalCopula（fitCopula（norm.cop,uv）@estimate）
+ dc = function（x,y）dCopula（cbind（x,y）,norm.cop）
+ ylab = names（dat）\[j\],zlab =“copule Gaussienne”,ticktype =“detailed”,zlim = zl）
+
+ t.cop < - tCopula（0.5,df = 3）
+ t.cop < - tCopula（t.fit \[1\],df = t.fit \[2\]）
+ ylab = names（dat）\[j\],zlab =“copule de Student”,ticktype =“detailed”,zlim = zl）
+}
Consider this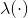 
function ,
Calculate the empirical version of three sequences , And compare it with some parameter versions ,
>
> lambda = function（C）{
+ l = function（u）pcopula（C,cbind（u,u））/ u
+ v = Vectorize（l）（u）
+ return（c（v,rev（v）））
+}
>
> graph_lambda = function（i,j）{
+ X = dat_res
+ U = rank（X \[,i\]）/（nrow（X）+1）
+ V = rank（X \[,j\]）/（nrow（X）+1）
+ normal.cop < - normalCopula（.5,dim = 2）
+ t.cop < - tCopula（.5,dim = 2,df = 3）
+ fit1 = fitCopula（normal.cop,cbind（U,V）,method =“ml”）
d（U,V）,method =“ml”）
+ C1 = normalCopula（fit1 @ copula @ parameters,dim = 2）
+ C2 = tCopula（fit2 @ copula @ parameters \[1\],dim = 2,df = trunc（fit2 @ copula @ parameters \[2\]））
+
But one might wonder if the correlation is stable over time .
> time\_varying\_correl_2 = function（i = 1,j = 2,
+ nom_arg =“Pearson”）{
+ uv = dat_arma \[,c（i,j）\]
nom_arg））\[1,2\]
+}
> time\_varying\_correl_2（1,2）
> time\_varying\_correl_2（1,2,“spearman”）
> time\_varying\_correl_2（1,2,“kendall”）
Spearman and time-varying rank correlation coefficient
Or Kendall The correlation coefficient
For the relevance of the model , consider DCC Model （S）
> m2 = dccFit（dat\_res\_std）
> m3 = dccFit（dat\_res\_std,type =“Engle”）
> R2 = m2 $ rho.t
> R3 = m3 $ rho.t
To get some predictions , Use, for example
> garch11.spec = ugarchspec（mean.model = list（armaOrder = c（2,1））,variance.model = list（garchOrder = c（1,1）,model =“GARCH”））
> dcc.garch11.spec = dccspec（uspec = multispec（replicate（3,garch11.spec））,dccOrder = c（1,1）,
distribution =“mvnorm”）
> dcc.fit = dccfit（dcc.garch11.spec,data = dat）
> fcst = dccforecast（dcc.fit,n.ahead = 200）
The most popular insights
2.R Sampling based on mixed data (MIDAS) Returning HAR-RV Model to predict GDP growth Returning HAR-RV Model to predict GDP growth ")
3. The realization of volatility ：ARCH Model and HAR-RV Model
5.GARCH（1,1）,MA And historical simulation VaR Compare
6.R Language diversity COPULA GARCH Model time series prediction
7.R Language based ARMA-GARCH Process of VAR Fitting and Forecasting
8.matlab forecast ARMA-GARCH Conditional mean and variance models
9.R Language pairs S＆P500 The stock index ARIMA + GARCH Trading strategies
