LeetCode·32.最长有效括号·栈·动态规划

链接：https://leetcode.cn/problems/longest-valid-parentheses/solution/by-xun-ge-v-h2qz/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。 

题目

 

示例

 

思路

解题思路

1. 栈

具体做法是我们始终保持栈底元素为当前已经遍历过的元素中「最后一个没有被匹配的右括号的下标」，这样的做法主要是考虑了边界条件的处理，栈里其他元素维护左括号的下标：

• 对于遇到的每个‘(’ ，我们将它的下标放入栈中
• 对于遇到的每个 ‘)’ ，我们先弹出栈顶元素表示匹配了当前右括号：

如果栈为空，说明当前的右括号为没有被匹配的右括号，我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
如果栈不为空，当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」
我们从前往后遍历字符串并更新答案即可。

需要注意的是，如果一开始栈为空，第一个字符为左括号的时候我们会将其放入栈中，这样就不满足提及的「最后一个没有被匹配的右括号的下标」，为了保持统一，我们在一开始的时候往栈中放入一个值为 −1 的元素。

1. 动态规划

结合题目，可以考虑尝试使用 动态规划 进行分析。这是一个 最值型 动态规划的题目。
动态规划题目分析的 4 个步骤：

• 确定状态
  • 研究最优策略的最后一步
  • 化为子问题
• 转移方程
  • 根据子问题定义得到
• 初始条件和边界情况
• 计算顺序

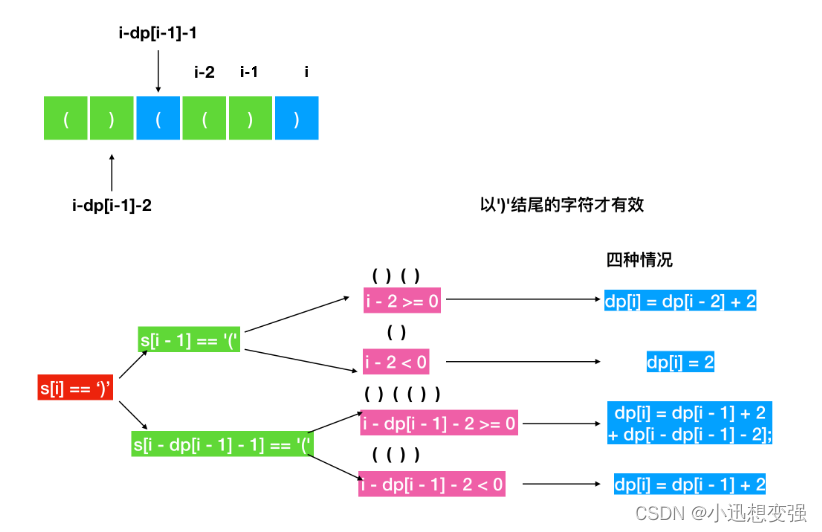
具体实现
首先，我们定义一个 dp 数组，其中第 i 个元素表示以下标为 i 的字符结尾的最长有效子字符串的长度。当i为 ')'时分析对于位置括号情况即可。 

代码

//栈
#define MAX(a , b) ((a) > (b) ? (a) : (b))
int longestValidParentheses(char * s){
    int len = strlen(s);
    int max = 0;
    int str[len+1];//定义栈
    int top = -1;
    str[++top] = -1;//定义标准
    for(int i = 0; i < len; i++)//遍历字符串
    {
        if(s[i] == '(')//入栈
        {
            str[++top] = i;
        }
        if(s[i] == ')')//出栈
        {
            --top;
            if(top == -1)//重新定义标准
            {
                str[++top] = i;
            }
            else
            {
                max = MAX(max , (i - str[top]));
            }
        }
    }
    return max;
}

作者：xun-ge-v
链接：https://leetcode.cn/problems/longest-valid-parentheses/solution/by-xun-ge-v-h2qz/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

//动态规划
#define MAX(a , b) ((a) > (b) ? (a) : (b))
int longestValidParentheses(char * s){
    int len = strlen(s);
    if(len == 0)
        return 0;
    int dp[len];
    memset(dp, 0, sizeof(int) * len);//初始化dp数组
    int max = 0;
    for(int i = 1; i < len; i++)//遍历字符串
    {
        if(s[i] == ')')//当s【i】 -> ')'分析
        {
            if(s[i - 1] == '(')
            {
                if(i-2 >= 0)
                {
                    dp[i] = dp[i-2] + 2;
                } 
                else
                {
                    dp[i] = 2;
                }
            }
            else if(i - dp[i-1] > 0 && s[i - dp[i-1] - 1] == '(')
            {
                if(i - dp[i-1] - 2 >= 0)
                {
                    dp[i] = dp[i-dp[i-1] - 2] + dp[i - 1] + 2;
                }
                else
                {
                    dp[i] =  dp[i - 1] + 2;
                }
            }
        }
        max = MAX(max , dp[i]);
    }
    return max;
}

作者：xun-ge-v
链接：https://leetcode.cn/problems/longest-valid-parentheses/solution/by-xun-ge-v-h2qz/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

 

时间空间复杂度