"C language" frog jumping steps recursion problem

Title:

A frog can jump 1 step at a time or jump 2 steps at a time. For example, there is only one way to jump to the first step: just jump 1 step directly.There are two ways to jump up two steps: one step at a time, two jumps; or two steps at a time. How many ways are there to jump to the nth step?

Thinking Analysis:

First of all, we can consider that the frog will only have one jumping method when there is only one step, and two jumping methods when there are two steps

                         

Then let's try to consider if there are three steps, the little frog can have a variety of choices, he can choose one by one

 

You can also choose to jump one step for the first time and jump two steps directly for the second time

 

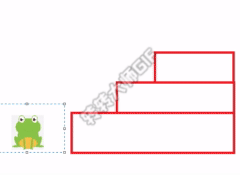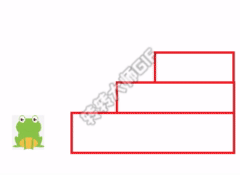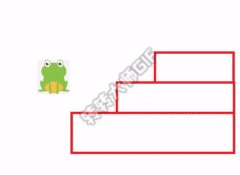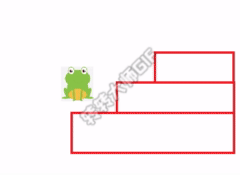
You can also choose to jump two steps for the first time, and then jump another step

 

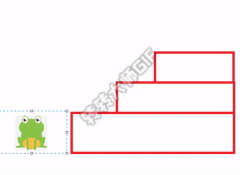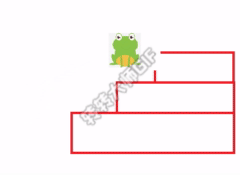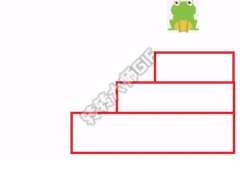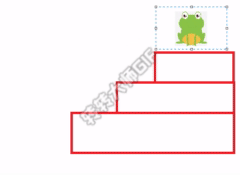
In summary, we can get

If there is a step, the little frog has a way of jumping;

If there are two steps, the frog can jump in two ways;

If there are three steps, the frog can jump in three ways;

If there are four steps, the frog can jump in five ways;

……………………

Then we can consider that the jumping method of the little frog is nothing more than the number of jumps of n-1 steps + the number of jumps of n-2 steps

So our code can look like this

int frog(int n) {if (n == 1)return 1;else if (n == 2)return 2;else return frog(n - 1) + frog(n - 2);}

Okay, I will share this idea here~~ Thank you for your support.