当前位置：网站首页>Leetcode: binary tree (4)

Leetcode: binary tree (4)

2020-11-10 10:44:00 【Jesse-jia】

This group consists of two binary trees How to find the sum of paths , Finally, make a little extension .

129. Sum Root to Leaf Numbers

Title Description : secondary

Solution 1 ：dfs

Each floor needs to be multiplied by 10, Recursive implementation , consider dfs;
Use one sum To save the sum of the current path , use ans To save the sum of all current paths
Every child node ,sum = The value of the child node +sum*10 As the current path , Until you reach the leaf node ,ans = ans+sum.

 1 class Solution:
 2     def sumNumbers(self, root: TreeNode) -> int: 
 3         if not root:
 4             return 0
 5         def dfs(root, sum): #  Recursive function , Enter the root node and sum, Output none , Constantly updated ans
 6             sum = root.val + sum * 10
 7             if not root.left and not root.right:
 8                 self.ans += sum
 9             if root.left:
10                 helper(root.left, sum)
11             if root.right:
12                 helper(root.right, sum)   
13         self.ans = 0 #  You can also define a global variable , It's just relative to the inner function dfs
14         dfs(root, 0)
15         return self.ans

112. Path Sum

Title Description : Simple

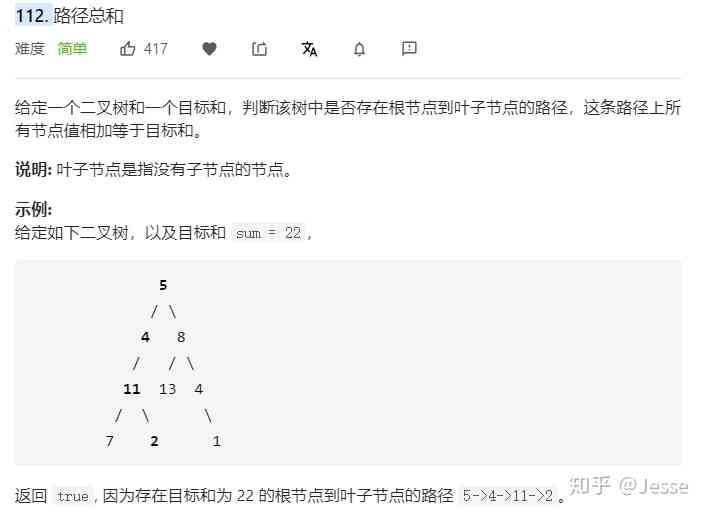
Solution 1 ： recursive

Traverse all nodes , Give Way sum = sum - The value of this node , Then let the child node of the node also call hasPahSum function , Until you reach the leaf node , final sum If 0, It means that such a path has been found ;

Binary tree recursion is very routine to follow , Generally speaking , When the node is done , The others will be handed back to us ;
And trees are left-right branches , So in the end, the recursive function is returned in general (left) (and/or) Recursive function (right) that will do .

 1 class Solution:
 2     def hasPathSum(self, root: TreeNode, sum: int) -> bool:
 3         if not root: #  Empty tree 
 4             return False
 5         sum -= root.val #  Every step recursion 
 6         if root.left == None and root.right == None: #  Recursion end condition 
 7             return (sum == 0)
 8         return self.hasPathSum(root.left, sum) or self.hasPathSum(root.right, sum) #  As long as there is a path for True that will do .
 9         #  Time complexity ： Visit each node once O(N).
10         #  Spatial complexity ： The worst case scenario when the tree is unbalanced is O(N). At best （ Trees are balanced ） Next is O(logN).

113. Path Sum II

Title Description : secondary

Solution 1 ： recursive

This problem requires that the path must start from the root node and reach the leaf node , So the idea is simple , take dfs:

Each time you enter recursion, you must first reduce the current node value , namely sum -= root.val

Recursive termination condition , If it's a leaf node (not root.left and not root.right), And path residue and sum = 0 了 , Add the result to the result array ;

If there are left subtrees , Recursive left subtree , Right subtree is the same ;

Be careful , Array in python Variable type in , there path+[root.val] It is equivalent to creating a new object on the stack , If you use append Indicates that no new object has been created, that is, the original object has been put on the stack , So make mistakes .

   

class Solution(object):
   def pathSum(self, root, sum):
       """
       :type root: TreeNode
       :type sum: int
       :rtype: List[List[int]]
       ""
       if not root: return []
       ans = []
       path = []
       def dfs(root, path, sum):  
           sum -= root.val
           if sum == 0 and not root.left and not root.right: #  Just change the line of business ：
               ans.append(path + [root.val])
           if root.left:
               dfs(root.left, path+ [root.val], sum)
           if root.right:
               dfs(root.right, path + [root.val], sum)
       dfs(root, path, sum) #  Think about the first value you pass in , You can get the termination condition 
       return ans

  

437. Path Sum III

Title Description : secondary

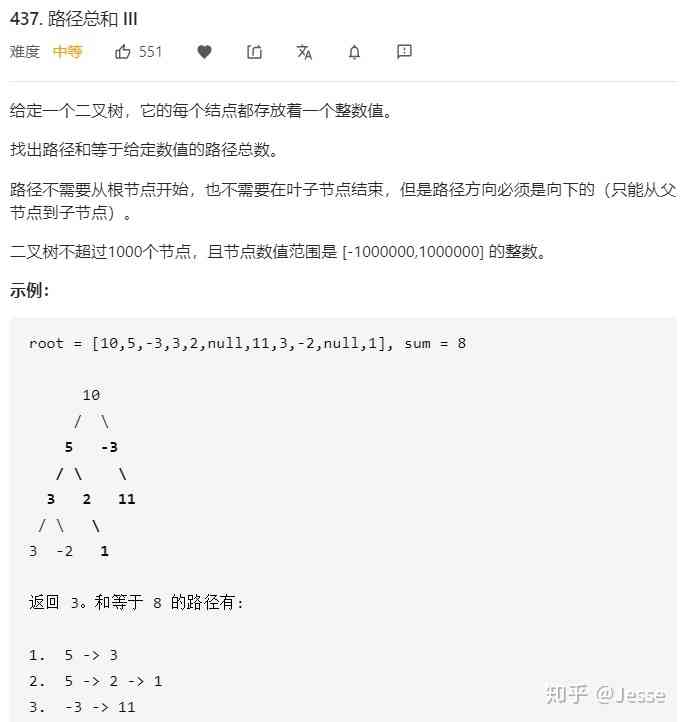
Solution 1 ： recursive

This problem requires a path that does not necessarily start from the root node and does not have to reach the leaf node , Just change your mind a little bit ：

First of all, every time you enter recursion, you must first reduce the current node value , namely sum -= root.val

Recursive termination condition , Because there is no need to reach the leaf node , All you need is path residue and sum = 0 了 , The number of programs is +1;

If there are left subtrees , Recursive left subtree , Right subtree is the same ;

The above recursive function is inner recursion , Its meaning is from any root node to find the path to meet the conditions , Of course, we also need an outer recursive function , Here is our main function pathSum, Its meaning is to find a path from a root node , After traversing all the root nodes as the starting point .

We need a global variable self.ans To record the results .

 1 class Solution(object):
 2     def __init__(self):
 3         self.ans = 0
 4     def pathSum(self, root, sum):
 5         #  recursive , Depth-first search 
 6         #  situation 3： It doesn't have to start at the root , It doesn't have to end with the leaves 
 7         #  First write down the number of such programs 
 8         #  Ideas ： Double recursion 
 9         #  The outer recursion should be 113 Take a certain point as the starting point to find the path 
10         #  Inner recursion starts at each point .
11         #  On this basis, the concrete solution can be realized .
12         def dfs(root, sum): #  Outer recursion , Take a point as a starting point to find a path 
13             # if not root: #  The end condition 
14             #     return
15             sum -= root.val
16             if sum == 0:
17                 self.ans += 1
18             if root.left:
19                 dfs(root.left, sum)
20             if root.right:
21                 dfs(root.right, sum)
22         #  The main function ：
23         #  The main function should not be set to zero every time self.res
24         if not root:
25             return self.ans
26         dfs(root, sum)
27         self.pathSum(root.left, sum)
28         self.pathSum(root.right, sum)
29         return self.ans

Expand

It's also the sum of similar paths , If we fix the root node , Path is defined as starting from the root , You don't need to reach the leaf node , To find out the specific path in this way .

Solution 1 ： recursive

This problem requires that the path must start from the root node, but not necessarily to the leaf node , The idea is still the same , Just change the termination condition of recursion ：

Only the path residue and sum = 0 了 , Just add the result to the result array ;

If there are left subtrees , Recursive left subtree , Right subtree is the same ;

The difference from the previous question is , There is no need for outer recursive functions for this problem ;

 1 class Solution(object):
 2     def pathSum(self, root, sum):
 3         """
 4         :type root: TreeNode
 5         :type sum: int
 6         :rtype: List[List[int]]
 7         ""
 8         if not root: return []
 9         ans = []
10         path = []
11         def dfs(root, path, sum):  
12             sum -= root.val
13             if sum == 0: #  Just change the line of business ：
14                 ans.append(path + [root.val])
15             if root.left:
16                 dfs(root.left, path+ [root.val], sum)
17             if root.right:
18                 dfs(root.right, path + [root.val], sum)
19         dfs(root, path, sum) #  Think about the first value you pass in , You can get the termination condition 
20         return ans