Informatics orsay a tong (1258: 【 9.2 】 digital pyramid)

1258: [Example 9.2] Digital Pyramid

Time Limit: 1000 ms Memory Limit: 65536 KB
Commits: 20019 Passes: 11518

【Title Description】

Observe the digital pyramid below.Write a program to find a path that ends anywhere from the highest point to the bottom, so that the sum of the paths passing through the numbers is the largest.Each step can go from the current point to the lower left point or to the lower right point.

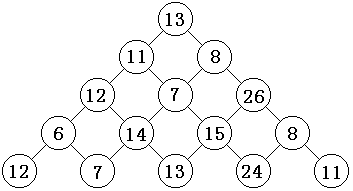
In the example above, the path from 13 to 8 to 26 to 15 to 24 yields the maximum sum of 86.

[Enter]

The first line contains R (1≤R≤1000), which indicates the number of lines.

Each subsequent row contains an integer for a particular row of this digital pyramid.

All integers supplied are non-negative and no greater than 100.

【Output】

A single line containing the largest possible sum.

【Sample input】

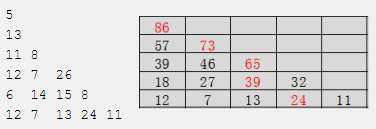
51311 812 7 266 14 15 812 7 13 24 11

【Example of output】

86

【Analysis】

Method 1: Push forward

Let a[i][j] store the number tower, and f[i][j] record the sum of the path numbers from the starting point to the jth column of the ith layer.

(1) Division into stages.

Stages: Each layer is a stage; there are five stages in the sample.

(2) Determine the state and state variables.

state: each value in the two-dimensional array is the state.Status information is represented by f[i][j].

(2) Determine the decision and write out the state transition equation.

Where does the value of f[i][j] come from?Of course from column j and column j-1 of row i-1 above.Decisions: From Above?Or from top left?, strategy: maximize the path.Therefore:

The state transition equation:

(4) Find boundary conditions.

When pushing forward, the boundary: f[1][1]=a[1][1].Goal: max(f[n][j])

(5) Design and implement programs.

[Reference code 1]

#include #define MAXN 1010int a[MAXN][MAXN]; //Store the tower dataint f[MAXN][MAXN]; //f[i][j] represents the sum of the path numbers from the starting point to the j column of the i layerint max(int ​​x,int y){return x > y ? x : y;}int main(){int i,j,n,ans;scanf("%d",&n);for(i=1;i<=n;i++)for(j=1;j<=i;j++)scanf("%d",&a[i][j]);f[1][1]=a[1][1];for(i=2;i<=n;i++)for(j=1;j<=i;j++)f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j]; //state transition equationans=0;for(i=1;i<=n;i++) //max(f[n][j])ans=max(ans,f[n][i]);printf("%d",ans);return 0;}

Method 2: Inverse method

Where does the value of f[i][j] come from when pushing backwards?is from column j and column j+1 of row i+1 below.The state transition equation is:

Boundary: f[n][j]=a[n][j].Target: f[1][1].

[Reference code 2]

#include #define MAXN 1010int a[MAXN][MAXN]; //Store the tower dataint f[MAXN][MAXN]; //f[i][j] represents the sum of the path numbers from the starting point to the j column of the i layerint max(int ​​x,int y){return x > y ? x : y;}int main(){int i,j,n;scanf("%d",&n);for(i=1;i<=n;i++)for(j=1;j<=i;j++)scanf("%d",&a[i][j]);for(i=1;i<=n;i++)f[n][i]=a[n][i];for(i=n-1;i>=1;i--)for(j=1;j<=i;j++)f[i][j]=max(f[i+1][j],f[i+1][j+1])+a[i][j]; //state transition equationprintf("%d",f[1][1]); //target f[1][1]return 0;}

http://ybt.ssoier.cn:8088/problem_show.php?pid=1258

a>