当前位置:网站首页>【ACWing】406. 放置机器人
【ACWing】406. 放置机器人
2022-08-01 23:47:00 【记录算法题解】
题目地址:
https://www.acwing.com/problem/content/description/408/
给出一个地图(网格),格子分为空地,草地,墙壁。要在空地上放能向上下左右 4 4 4个方向发射激光的机器人。墙壁能挡住激光,草地不能挡住激光也不能放机器人。在机器人不能互相打到对方的情况下,最多放置多少个机器人。
输入格式:
第一行包含整数 T T T,表示共有 T T T组测试数据。
每组数据第一行包含两个整数 m m m和 n n n,表示地图的大小为 m m m行 n n n列。
接下来 m m m行,每行包含 n n n个字符,用来描述整个地图。#代表墙壁,*代表草地,o代表空地。
输出格式:
每组测试数据在第一行输出Case :id,id是数据编号,从 1 1 1开始。
第二行包含一个整数,表示机器人的个数。
数据范围:
1 ≤ m , n ≤ 50 1≤m,n≤50 1≤m,n≤50
思路是二分图。将除了墙的地面定义一个等价关系叫行连通,两个非墙地面行连通当且仅当从一个能沿着行不经过墙走到另一个。那么这个等价关系可以将所有的非墙地面分为若干个等价类,我们把这些等价类编号为 1 , 2 , . . . , r 1,2,...,r 1,2,...,r;同理将列连通等价类编号为 1 , 2 , . . . , c 1,2,...,c 1,2,...,c。将 1 , 2 , . . . , r 1,2,...,r 1,2,...,r视为二分图左边的点, 1 , 2 , . . . , c 1,2,...,c 1,2,...,c视为二分图右边的点,如果某个行连通块和某个列连通块有交集,并且交集是o即空地,则将他们的编号之间连一条边。首先,这个二分图的任何一个匹配对应着一种放置方案:每条边对应一个空地,并且同一个行连通块里只能有一个机器人(因为会互相攻击),同一个列连通块也只能有一个机器人。其次,任意一个放置方案,对应一个匹配。所以最多的机器人放置方案一定就是二分图的最大匹配,从而可以用匈牙利算法来做。代码如下:
#include <cstring>
#include <iostream>
using namespace std;
const int N = 55, M = 2550;
int n, m, rcnt, ccnt;
char a[N][N];
int rid[N][N], cid[N][N];
int match[M];
bool vis[M];
int h[M], e[M], ne[M], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool dfs(int u) {
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (vis[v]) continue;
vis[v] = true;
if (!match[v] || dfs(match[v])) {
match[v] = u;
return true;
}
}
return false;
}
int main() {
int T;
scanf("%d", &T);
for (int t = 1; t <= T; t++) {
memset(h, -1, sizeof h);
idx = 0;
memset(rid, 0, sizeof rid);
memset(cid, 0, sizeof cid);
scanf("%d%d", &m, &n);
for (int i = 1; i <= m; i++) scanf("%s", a[i] + 1);
rcnt = 1, ccnt = 1;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++) {
if (a[i][j] != '#') {
while (j <= n && a[i][j] != '#') rid[i][j++] = rcnt;
rcnt++;
}
}
for (int j = 1; j <= n; j++)
for (int i = 1; i <= m; i++) {
if (a[i][j] != '#') {
while (i <= m && a[i][j] != '#') cid[i++][j] = ccnt;
ccnt++;
}
}
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
if (a[i][j] == 'o') add(rid[i][j], cid[i][j]);
int res = 0;
memset(match, 0, sizeof match);
// 行连通块的个数为rcnt - 1
for (int i = 1; i < rcnt; ++i) {
memset(vis, 0, sizeof vis);
if (dfs(i)) res++;
}
printf("Case :%d\n%d\n", t, res);
}
}
每组数据时间复杂度 O ( ( m n ) 2 ) O((mn)^2) O((mn)2),空间 O ( m n ) O(mn) O(mn)。
边栏推荐
- 获取小猪民宿(短租)数据
- 类型“FC<Props>”的参数不能赋给类型“ForwardRefRenderFunction<unknown, Props>”的参数。 属性“defaultProps”的类型不兼容。 不
- UML diagram of soft skills
- 字节跳动面试官:请你实现一个大文件上传和断点续传
- ansible模块--copy模块
- 根本上解决mysql启动失败问题Job for mysqld.service failed because the control process exited with error code
- What can be done to make this SQL into a dangerous SQL?
- Special characters & escapes in bat
- numpy.unique
- cdh6 opens oozieWeb page, Oozie web console is disabled.
猜你喜欢

Secondary Vocational Network Security Competition B7 Competition Deployment Process

如何进行数据库备份
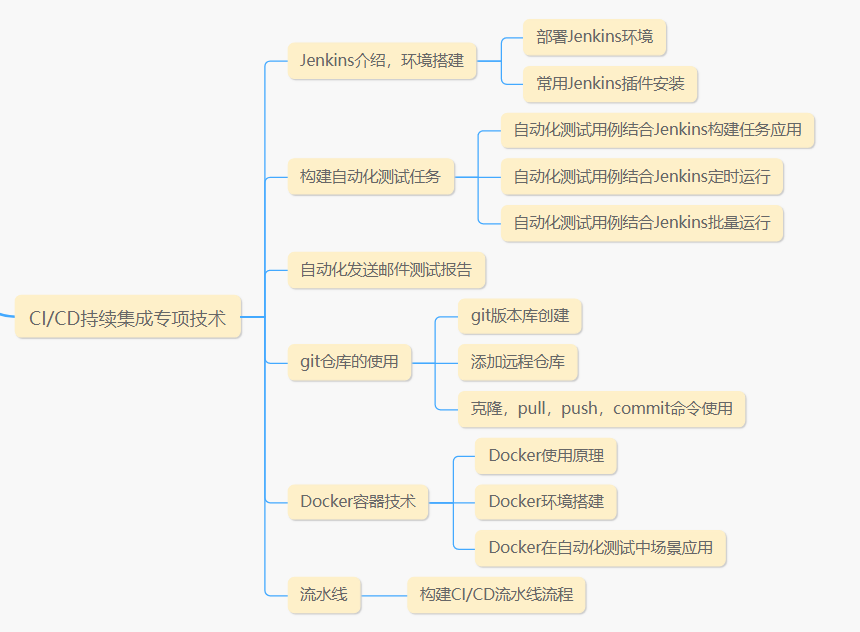
2022还想上岸学习软件测试必看,测试老鸟的肺腑之言...

数据机构---第五章树与二叉树---二叉树的概念---应用题
GIF制作-灰常简单的一键动图工具

oozie startup error on cdh's hue, Cannot allocate containers as requested resource is greater than maximum allowed

20220725 Information update

ICLR 2022最佳论文:基于对比消歧的偏标签学习

WEB安全基础 - - - XRAY使用
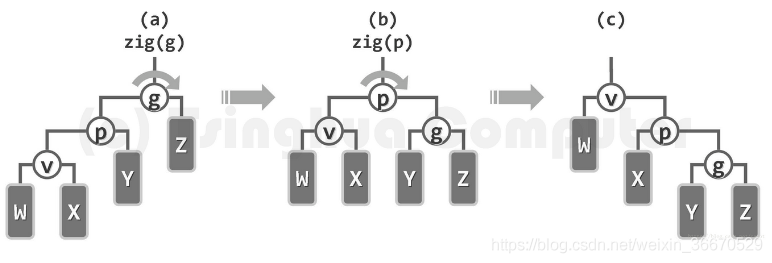
伸展树的特性及实现
随机推荐
洞见云原生微服务及微服务架构浅析
ansible模块--copy模块
ELK日志采集
Flink Yarn Per Job - CliFrontend
UI自动化测试框架搭建-标记性能较差用例
With a monthly salary of 12K, the butterfly changed to a new one and moved forward bravely - she doubled her monthly salary through the career change test~
Spark Sql之union
Programmer is still short of objects? A new one is enough
thinkphp漏洞总结
chrome copies the base64 data of an image
Check if point is inside rectangle
Solve the port to take up
斜堆、、、
Oracle database is set to read-only and read-write
[C language advanced] file operation (2)
LocalDateTime转为Date类型
Chapter 12 End-User Task As Shell Scripts
在CDH的hue上的oozie出现,提交 Coordinator My Schedule 时出错
@Resource和@Autowired的区别
@Scheduled注解详解