当前位置:网站首页>[combinatorics] brief introduction to generating function (definition of generating function | Newton binomial coefficient | commonly used generating function | correlation with constant | correlation
[combinatorics] brief introduction to generating function (definition of generating function | Newton binomial coefficient | commonly used generating function | correlation with constant | correlation
2022-07-03 03:24:00 【Programmer community】
List of articles
- One . Generating function ( The generating function ) The definition of
- 1. Generating function definition
- ( 1 ) Definition of generating function
- ( 2 ) Formal power series ( Reference resources )
- 2. Generating function Example
- ( 1 ) Generating function Example 1 (
a
n
=
(
m
n
)
a_n = \dbinom{m}{n}
an=(nm) )
- ( 2 ) Generating function Example 2 (
{
k
n
}
\{k^n\}
{ kn} )
- ( 1 ) Generating function Example 1 (
- 2. Newton binomial
- ( 1 ) Newton binomial coefficient
- ( 2 ) Newton binomial Theorem
- Two . Commonly used Generating function ( important )
- 1. Generating functions related to constants
- ( 1 )
{
1
n
}
\{1^n\}
{ 1n} Of Generating function
- ( 2 )
{
(
−
1
)
n
}
\{(-1)^n\}
{ (−1)n} Of Generating function
- ( 3 )
{
k
n
}
\{k^n\}
{ kn} (
k
k
k As a positive integer ) Of Generating function
- ( 1 )
- 2. And Binomial coefficient Related generating functions
- ( 1 )
{
(
m
n
)
}
\{\dbinom{m}{n}\}
{ (nm)} Of Generating function
- ( 1 )
- 3. And Combinatorial number Related generating functions
- ( 1 )
{
(
m
+
n
−
1
n
)
}
\{\dbinom{m+n-1}{n}\}
{ (nm+n−1)} Of Generating function
- ( 2 )
{
(
−
1
)
n
(
m
+
n
−
1
n
)
}
\{(-1)^n \dbinom{m+n-1}{n}\}
{ (−1)n(nm+n−1)} Of Generating function
- ( 3 )
{
(
n
+
1
1
)
}
\{ \dbinom{n+1}{1}\}
{ (1n+1)} Of Generating function
- ( 1 )
One . Generating function ( The generating function ) The definition of
1. Generating function definition
( 1 ) Definition of generating function
Generating function definition :
- 1. Assumptions : set up
a
0
,
a
1
,
⋯
,
a
n
a_0 , a_1 , \cdots , a_n
a0,a1,⋯,an It's a sequence ;
- 2. Formal power series : Use The The sequence do Formal power series
A
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
⋯
+
a
n
x
n
+
⋯
A(x) = a_0 + a_1x +a_2x^2 + \cdots + a_nx^n + \cdots
A(x)=a0+a1x+a2x2+⋯+anxn+⋯
- 3. Generating function : Call the above
A
(
x
)
A(x)
a
0
,
a
1
,
⋯
,
a
n
a_0 , a_1 , \cdots , a_n
a0,a1,⋯,an Of Generating function ;
A(x) yes The sequence
( 2 ) Formal power series ( Reference resources )
Formal power series :
- 1. Power series : Mathematical analysis in Important concepts , stay Exponential in every particular Are all And Series term Serial number
n
n
(
x
−
a
)
(x-a)
(x−a) Of
n
n
n Power (
n
n
n It's from
0
0
0 Integer to start counting ,
a
a
a Constant ) ;
- Use of power series : Its By As Basic content Applied to Real variable function , Complex functions , And so on in ;
n Corresponding With Constant times
- 2. Formal power series : yes In Mathematics Of Lottery concept , from Power series in Pulled out Of Algebraic objects ; Formal power series and from polynomial in Stripped out of Polynomial rings similar , however Its allow Infinite polynomial factor Add up , But not like Power series commonly requirement Research Convergence or not and Is there any definite Value ;
- ① Assumptions : set up
x
x
x It's a symbol ,
a
i
(
i
=
0
,
1
,
2
,
⋯
)
a_i ( i = 0 , 1 , 2 , \cdots )
ai(i=0,1,2,⋯) It's a real number ;
- ② Undetermined element Formal power series :
A
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
⋯
+
a
n
x
n
+
⋯
=
∑
n
=
0
∞
A(x) = a_0 + a_1x + a_2x^2 + \cdots + a_nx^n + \cdots = \sum_{n=0}^{\infty}
A(x)=a0+a1x+a2x2+⋯+anxn+⋯=n=0∑∞ be called
x
x
x Indeterminate element of Of One Formal power series ;
- ① Assumptions : set up
- 3. Research focus : Formal power series in ,
x
x
x never No specific value is specified , No concern convergence or Divergence , The focus is on its Coefficient sequence
a
0
,
a
1
,
⋯
,
a
n
a_0 , a_1 , \cdots , a_n
a0,a1,⋯,an , Study formal power series Absolutely. It comes down to Discuss These coefficient sequences ;
2. Generating function Example
( 1 ) Generating function Example 1 ( a
n
=
(
m
n
)
a_n = \dbinom{m}{n}
an=(nm) )
Example topic : set up
a
n
=
(
m
n
)
a_n = \dbinom{m}{n}
an=(nm) ,
m
m
m As a positive integer , Find the sequence
{
a
n
}
\{a_n\}
{ an} The generating function of
A
(
x
)
A(x)
A(x) ;
Explain :
① List generation functions :
A
(
x
)
=
(
m
0
)
x
0
+
(
m
1
)
x
1
+
(
m
2
)
x
2
+
⋯
+
(
m
n
)
x
n
A(x) = \dbinom{m}{0}x^0 + \dbinom{m}{1}x^1 + \dbinom{m}{2}x^2 + \cdots + \dbinom{m}{n}x^n
A(x)=(0m)x0+(1m)x1+(2m)x2+⋯+(nm)xn
② List their cumulative generating functions :
A
(
x
)
=
∑
n
=
0
∞
(
m
n
)
x
n
A(x) = \sum_{n=0}^\infty \dbinom{m}{n}x^n
A(x)=n=0∑∞(nm)xn
③ When
n
n
n Greater than
m
m
m when , from
m
m
m in take
n
n
n , namely
(
m
n
)
\dbinom{m}{n}
(nm) by 0 , So you can Direct calculation from
n
=
0
n=0
n=0 To
n
=
m
n=m
n=m Value , namely Get the following steps :
A
(
x
)
=
∑
n
=
0
∞
(
m
n
)
x
n
=
∑
n
=
0
m
(
m
n
)
x
n
A(x) = \sum_{n=0}^\infty \dbinom{m}{n}x^n = \sum_{n=0}^m \dbinom{m}{n}x^n
A(x)=n=0∑∞(nm)xn=n=0∑m(nm)xn
④ according to binomial theorem Inference content ( set up
n
n
n It's a positive integer. , For everything
x
x
x Yes
(
1
+
x
)
n
=
∑
k
=
0
n
(
n
k
)
x
k
(1+x)^n=\sum_{k=0}^n\dbinom{n}{k}x^k
(1+x)n=∑k=0n(kn)xk ) You can get
A
(
x
)
=
∑
n
=
0
∞
(
m
n
)
x
n
=
∑
n
=
0
m
(
m
n
)
x
n
=
(
1
+
x
)
m
A(x) = \sum_{n=0}^\infty \dbinom{m}{n}x^n = \sum_{n=0}^m \dbinom{m}{n}x^n = (1 + x)^m
A(x)=n=0∑∞(nm)xn=n=0∑m(nm)xn=(1+x)m
⑤ The sequence
a
n
=
(
m
n
)
a_n = \dbinom{m}{n}
an=(nm) (
m
m
m As a positive integer ) , Of Generating function by :
A
(
x
)
=
(
1
+
x
)
m
A(x) = (1 + x)^m
A(x)=(1+x)m
Be careful : Generating function be subordinate to A sequence of , When generating functions , First, explain the sequence , To specify The sequence Of Generating function yes Some function ;
( 2 ) Generating function Example 2 ( {
k
n
}
\{k^n\}
{ kn} )
subject : Given Positive integer
k
k
k , seek
{
k
n
}
\{k^n\}
{ kn} The generating function of ;
① Write the generating function : take
{
k
n
}
\{k^n\}
{ kn} As a formal power series coefficient , You can get as follows Geometric series , When
x
x
x When I was young enough , It converges to
1
1
−
k
x
\frac{1}{1-kx}
1−kx1 ;
A
(
x
)
=
k
0
x
0
+
k
1
x
1
+
k
2
x
2
+
k
3
x
3
+
⋯
=
1
1
−
k
x
A(x) = k^0x^0 + k^1x^1 + k^2x^2 + k^3x^3 + \cdots = \frac{1}{1-kx}
A(x)=k0x0+k1x1+k2x2+k3x3+⋯=1−kx1
②
{
k
n
}
\{k^n\}
{ kn} In sequence Generating function by :
A
(
x
)
=
1
1
−
k
x
A(x) = \frac{1}{1-kx}
A(x)=1−kx1
2. Newton binomial
( 1 ) Newton binomial coefficient
Newton binomial coefficient : Expansion of combinatorial number ,
C
(
m
,
n
)
C(m, n)
C(m,n) The previous item is no longer greater than or equal to
n
n
n The number of the , But any real number ;
- 1. Conditions : arbitrarily The set of real Numbers
r
r
n
n
n ;
r , and Integers
- 2. The formula :
(
r
n
)
=
{
0
,
n
<
0
1
,
n
=
0
r
(
r
−
1
)
⋯
(
r
−
n
+
1
)
n
!
,
n
>
0
\dbinom{r}{n} = \begin{cases} 0, & n < 0 \\ 1, & n=0 \\ \cfrac{r(r-1)\cdots(r-n+1)}{n!}, & n>0 \end{cases}
(nr)=⎩⎪⎪⎨⎪⎪⎧0,1,n!r(r−1)⋯(r−n+1),n<0n=0n>0
- 3. Conclusion : The
(
r
n
)
\dbinom{r}{n}
(nr) No, Combined meaning , It's just mark , be called Newton's binomial coefficient ;
Select the question :
- Non repeatable elements , Orderly selection , Corresponding Arrangement of sets ;
P
(
n
,
r
)
=
n
!
(
n
−
r
)
!
P(n,r) = \dfrac{n!}{(n-r)!}
P(n,r)=(n−r)!n!
- Non repeatable elements , Unordered selection , Corresponding A combination of sets ;
C
(
n
,
r
)
=
P
(
n
,
r
)
r
!
=
n
!
r
!
(
n
−
r
)
!
C(n,r) = \dfrac{P(n,r)}{r!} = \dfrac{n!}{r!(n-r)!}
C(n,r)=r!P(n,r)=r!(n−r)!n!
- Repeatable elements , Orderly selection , Corresponding Arrangement of multiple sets ;
whole
row
Column
=
n
!
n
1
!
n
2
!
⋯
n
k
!
Full Permutation = \cfrac{n!}{n_1! n_2! \cdots n_k!}
whole row Column =n1!n2!⋯nk!n! , Incomplete permutation
k
r
,
r
≤
n
i
k^r , \ \ r\leq n_i
kr, r≤ni
- Repeatable elements , Unordered selection , Corresponding Combination of multiple sets ;
N
=
C
(
k
+
r
−
1
,
r
)
N= C(k + r - 1, r)
N=C(k+r−1,r)
( 2 ) Newton binomial Theorem
Newton's binomial theorem :
- 1. Conditions :
α
\alpha
x
,
y
x , y
x,y , also
∣
x
y
∣
<
1
\left| \frac{x}{y} \right| < 1
∣∣∣yx∣∣∣<1 ;
α by The set of real Numbers , For everything
- 2. Conclusion :
(
x
+
y
)
α
=
∑
n
=
0
∞
(
α
n
)
x
α
y
α
−
n
( x + y ) ^ \alpha = \sum^{\infty}_{n=0}\dbinom{\alpha}{n}x^\alpha y^{\alpha - n}
(
α
n
)
=
α
(
α
−
1
)
⋯
(
α
−
n
+
1
)
n
!
\dbinom{\alpha}{n} = \frac{\alpha(\alpha-1)\cdots(\alpha-n+1)}{n!}
(nα)=n!α(α−1)⋯(α−n+1)
(x+y)α=n=0∑∞(nα)xαyα−n among
- 3. And binomial theorem Relationship : Newton's binomial theorem yes binomial theorem Of Extension , Binomial theorem is Newton's binomial theorem Of special case ;
- ① When
α
=
m
\alpha = m
α=m , And
m
m
n
>
m
n > m
n>m when ,
(
m
n
)
=
0
\dbinom{m}{n}=0
(nm)=0 , So just think about
n
<
m
n<m
n<m The situation of , here Newton's binomial theorem become binomial theorem :
(
x
+
y
)
m
=
∑
n
=
0
m
(
m
n
)
x
m
y
m
−
n
( x + y ) ^ m = \sum^{m}_{n=0}\dbinom{m}{n}x^m y^{m - n}
(x+y)m=n=0∑m(nm)xmym−n
(
1
+
x
)
m
=
∑
n
=
0
m
(
m
n
)
x
m
y
m
−
n
( 1 + x ) ^ m = \sum^{m}_{n=0}\dbinom{m}{n}x^m y^{m - n}
(1+x)m=n=0∑m(nm)xmym−n
m When it is a positive integer , When
- ① When
Two . Commonly used Generating function ( important )
1. Generating functions related to constants
( 1 ) {
1
n
}
\{1^n\}
{ 1n} Of Generating function
Common generating functions :
- 1. Formal power series ( The sequence ) :
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
1
n
a_n = 1^n
an=1n ;
- 2. Generate function expansion :
A
(
x
)
=
∑
n
=
0
∞
x
n
=
1
1
−
x
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} x^n \\ & = \frac{1}{1-x} \end{aligned}
A(x)=n=0∑∞xn=1−x1
( 2 ) {
(
−
1
)
n
}
\{(-1)^n\}
{ (−1)n} Of Generating function
Common generating functions :
- 1. Formal power series ( The sequence ) :
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
(
−
1
)
n
a_n = (-1)^n
an=(−1)n ;
- 2. Generate function expansion :
A
(
x
)
=
∑
n
=
0
∞
(
−
1
)
n
x
n
=
1
1
+
x
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} (-1)^n x^n \\ & = \frac{1}{1+x} \end{aligned}
A(x)=n=0∑∞(−1)nxn=1+x1
( 3 ) {
k
n
}
\{k^n\}
{ kn} (
k
k
k As a positive integer ) Of Generating function
Common generating functions :
- 1. Formal power series ( The sequence ) :
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
k
n
a_n = k^n
an=kn ,
k
k
k As a positive integer ;
- 2. Generate function expansion :
A
(
x
)
=
∑
n
=
0
∞
k
n
x
n
=
1
1
−
k
x
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} k^n x^n \\ & = \frac{1}{1-kx} \end{aligned}
A(x)=n=0∑∞knxn=1−kx1
2. And Binomial coefficient Related generating functions
( 1 ) {
(
m
n
)
}
\{\dbinom{m}{n}\}
{ (nm)} Of Generating function
Common generating functions :
- 1. Formal power series ( The sequence ) :
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
(
m
n
)
a_n = \dbinom{m}{n}
an=(nm)
- 2. Generate function expansion :
A
(
x
)
=
∑
n
=
0
∞
(
m
n
)
x
n
=
(
1
+
x
)
m
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} \dbinom{m}{n} x^n \\ & = ( 1 + x ) ^m \end{aligned}
A(x)=n=0∑∞(nm)xn=(1+x)m
3. And Combinatorial number Related generating functions
( 1 ) {
(
m
+
n
−
1
n
)
}
\{\dbinom{m+n-1}{n}\}
{ (nm+n−1)} Of Generating function
Common generating functions :
- 1. Formal power series ( The sequence ) :
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
(
m
+
n
−
1
n
)
a_n = \dbinom{m+n-1}{n}
an=(nm+n−1) ,
m
,
n
m,n
m,n As a positive integer ;
- 2. Generate function expansion :
A
(
x
)
=
∑
n
=
0
∞
(
m
+
n
−
1
n
)
x
n
=
1
(
1
−
x
)
m
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} \dbinom{m+n-1}{n} x^n \\ & = \frac{1}{ {(1-x)}^m} \end{aligned}
A(x)=n=0∑∞(nm+n−1)xn=(1−x)m1
( 2 ) {
(
−
1
)
n
(
m
+
n
−
1
n
)
}
\{(-1)^n \dbinom{m+n-1}{n}\}
{ (−1)n(nm+n−1)} Of Generating function
Common generating functions :
- 1. Formal power series ( The sequence ) :
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
(
−
1
)
n
(
m
+
n
−
1
n
)
a_n = (-1)^n \dbinom{m+n-1}{n}
an=(−1)n(nm+n−1) ,
m
,
n
m,n
m,n As a positive integer ;
- 2. Generate function expansion :
A
(
x
)
=
∑
n
=
0
∞
(
−
1
)
n
(
m
+
n
−
1
n
)
x
n
=
1
(
1
+
x
)
m
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} (-1)^n \dbinom{m+n-1}{n} x^n \\ & = \frac{1}{ {(1+x)}^m} \end{aligned}
A(x)=n=0∑∞(−1)n(nm+n−1)xn=(1+x)m1
( 3 ) {
(
n
+
1
1
)
}
\{ \dbinom{n+1}{1}\}
{ (1n+1)} Of Generating function
Common generating functions :
- 1. Formal power series ( The sequence ) :
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
(
n
+
1
n
)
a_n = \dbinom{n+1}{n}
an=(nn+1) ,
n
n
n As a positive integer ;
- 2. Generate function expansion :
A
(
x
)
=
∑
n
=
0
∞
(
n
+
1
n
)
x
n
=
∑
n
=
0
∞
(
n
+
1
)
x
n
=
1
(
1
−
x
)
2
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} \dbinom{n+1}{n} x^n \\ & = \sum_{n=0}^{\infty} (n+1) x^n \\ & = \frac{1}{ {(1-x)}^2} \end{aligned}
A(x)=n=0∑∞(nn+1)xn=n=0∑∞(n+1)xn=(1−x)21
边栏推荐
- Pat class B "1104 forever" DFS optimization idea
- Vs 2019 installation and configuration opencv
- Spark on yarn资源优化思路笔记
- 敏捷认证(Professional Scrum Master)模拟练习题
- 敏捷认证(Professional Scrum Master)模拟练习题-2
- UMI route interception (simple and rough)
- L'index des paramètres d'erreur est sorti de la plage pour les requêtes floues (1 > Nombre de paramètres, qui est 0)
- 模型转换onnx2engine
- MySql實戰45講【SQL查詢和更新執行流程】
- Elsevier latex 提交文章 pdftex.def Error: File `thumbnails/cas-email.jpeg‘ not found: using draf
猜你喜欢

I2C subsystem (I): I2C spec
MongoDB安装 & 部署
Hi3536c v100r001c02spc040 cross compiler installation

docker安装mysql
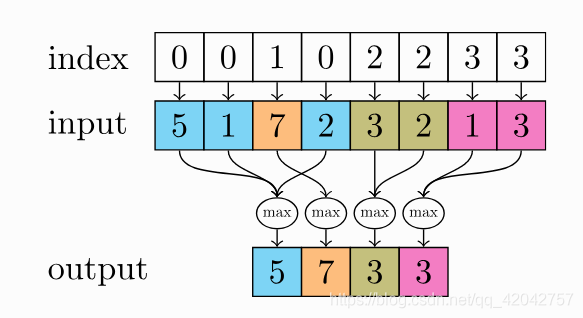
【PyG】理解MessagePassing过程,GCN demo详解

Nce detail of softmax approximation

Idea set method call ignore case
![C programming learning notes [edited by Mr. Tan Haoqiang] (Chapter III sequence programming) 03 operators and expressions](/img/4a/1df03d9f3315debb4c335260ed39f2.jpg)
C programming learning notes [edited by Mr. Tan Haoqiang] (Chapter III sequence programming) 03 operators and expressions
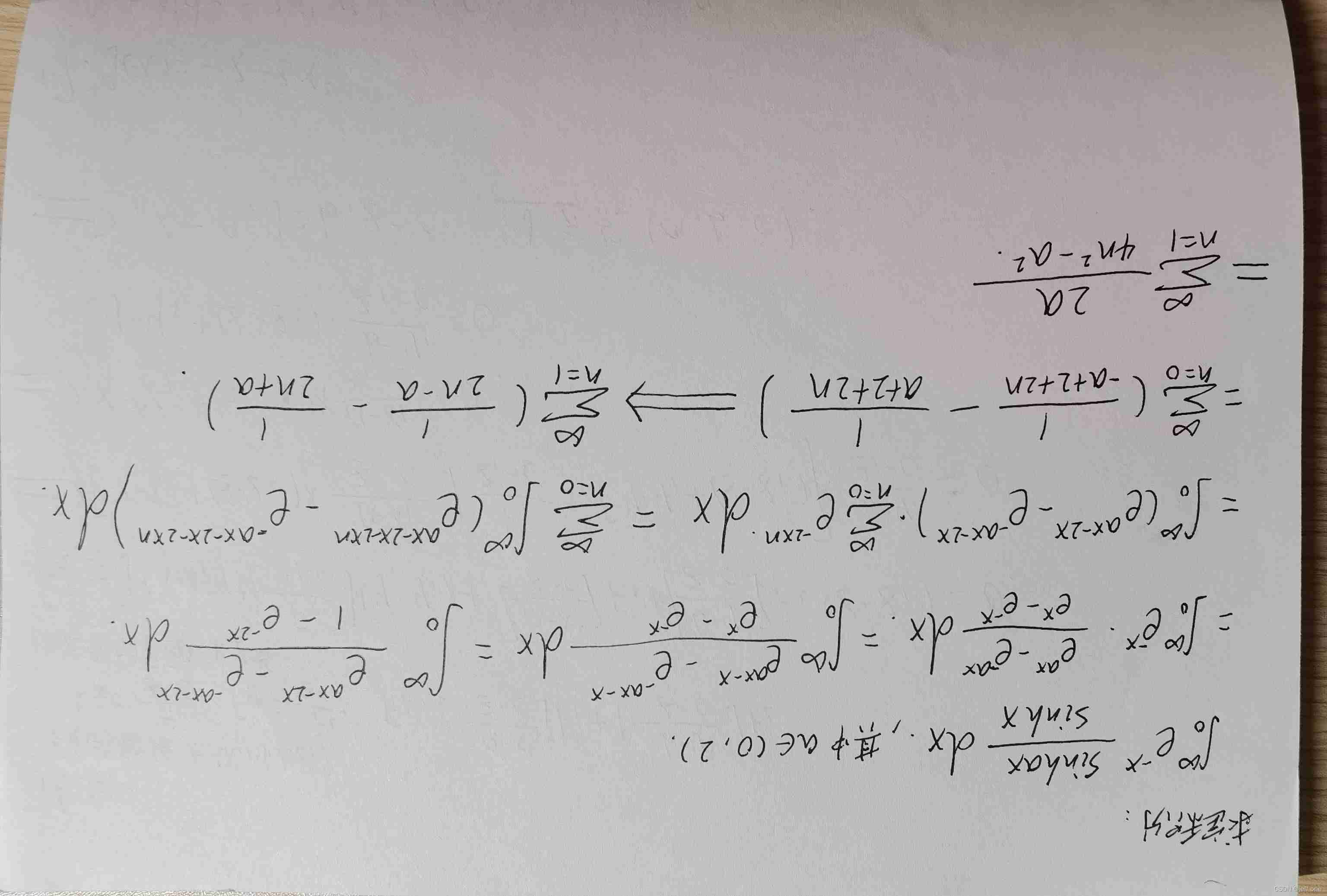
The series of hyperbolic function in daily problem

UMI route interception (simple and rough)
随机推荐
用Three.js做一个简单的3D场景
[combinatorics] basic counting principle (addition principle | multiplication principle)
C # webrequest post mode, based on "basic auth" password authentication mode, uploads files and submits other data using multipart / form data mode
C programming learning notes [edited by Mr. Tan Haoqiang] (Chapter III sequence programming) 05 data input and output
com. fasterxml. jackson. databind. Exc.invalidformatexception problem
float与0比较
机械臂速成小指南(八):运动学建模(标准DH法)
Réglez la hauteur et lancez le système. Currenttimemillis catton
MySQL practice 45 [global lock and table lock]
docker安装redis
PAT乙级“1104 天长地久”DFS优化思路
C # general interface call
MongoDB基本操作【增、删、改、查】
Node start server
Solve high and send system Currenttimemillis Caton
PHP constructor with parameters - PHP constructor with a parameter
Creation and destruction of function stack frame
Limit of one question per day
Vs Code configure virtual environment
Introduction à mongodb