Li Hongyi machine learning (2021 Edition)_ P5-6: small gradient processing

Related information

Video link ：https://www.bilibili.com/video/BV1JA411c7VT

Original video link ：https://speech.ee.ntu.edu.tw/~hylee/ml/2021-spring.html

Leeml-notes Open source project ：https://github.com/datawhalechina/leeml-notes

1、 Optimization failure reason Optimization Fails

1.1、critical point

gradient is zero, The gradient of 0 The point of , be called critical point. Contains two categories ,local minima,saddle point, as follows ：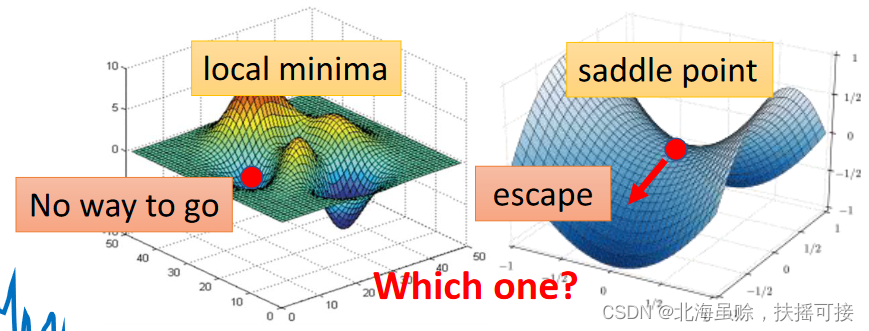

1.2、 Mathematical explanation

Using multivariate function Taylor expansion ,𝐿（𝜽） stay 𝜽 = 𝜽′ Expand as follows ：

g Is the gradient of function , It's a vector ;H Hessian matrix of function , Express the second-order matrix for different parameters ：

stay critical point It's about , gradient g=0, Simplified as follows ：

Critical Point There are three types ,minima,maxima,Saddle point, rely on ${\mathbf{v}}^{T}H\mathbf{v}$ Size judgment ：
${\mathbf{v}}^{T}H\mathbf{v}$>0：𝐿(𝜽)> 𝐿(𝜽′),minima
${\mathbf{v}}^{T}H\mathbf{v}$<0：𝐿(𝜽)< 𝐿(𝜽′),maxima
${\mathbf{v}}^{T}H\mathbf{v}$>0 And <0：Saddle point
It can also be done through H Positive and negative eigenvalues of Judge three kinds of special points . give an example ：$y=w_1{w}_{2}x$, data （1,1）
Loss function ：$L=(\hat{y}-w_1{w}_{2}x{)}^2=(1-w_1{w}_2{)}^2$;
Calculation g And H as follows ：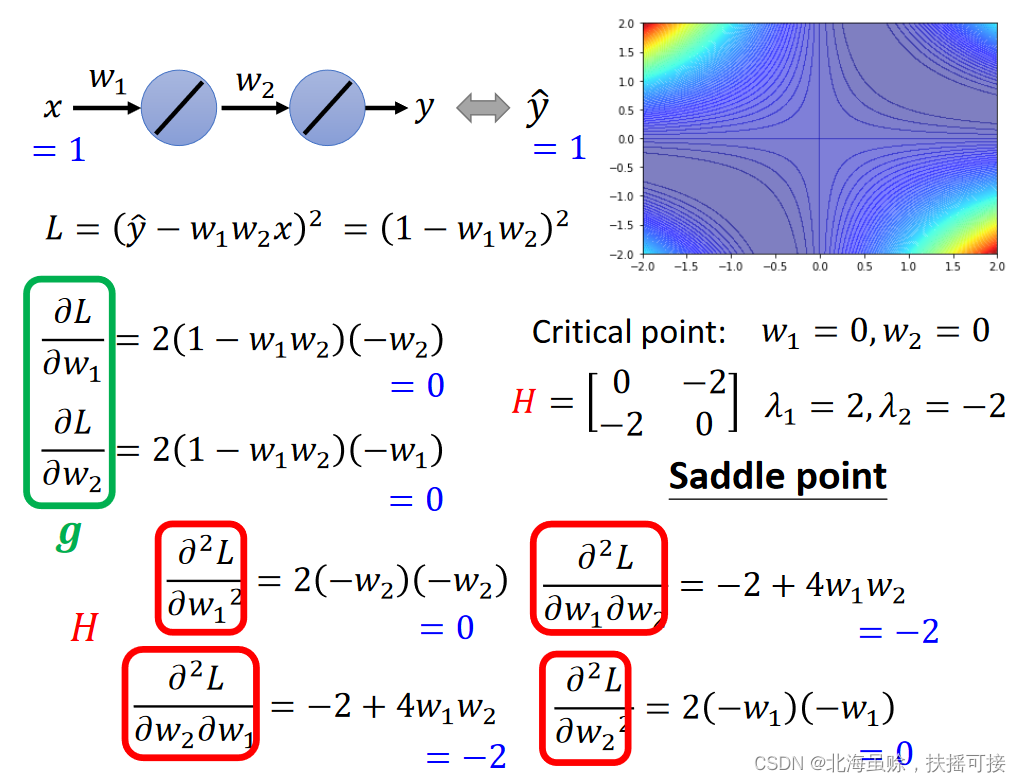

1.3、 Saddle point treatment

Rely on Hessian matrix H Determine the optimization direction of saddle point ,𝐻 may tell us parameter update direction. The hypothetical reasoning of mathematics is as follows ：

Looking for Hessian matrix H A negative eigenvector of u, That is to say L Direction of descent .
give an example ：
The above functions , Find the saddle point and find the direction of descent ：

• stay （0,0）, Hazen matrix H The eigenvalue 2,-2. There are positive and negative , Judge （0,0） For saddle point .
• Select Hessian matrix H The eigenvalue -2 Corresponding to an eigenvector 𝒖 = [1, 1], That is, the update direction .
  however , Because the amount of calculation is relatively large , The above methods are rarely used .
  

1.4、 Proportion of critical points

$Minimumratio=\frac{NumberofPositiveEigenvalues}{NumberofEigenvalues}$
Above picture , Through empirical research , Most of critical point For saddle point ,local minima Very few ( Abscissa 1 It's about , It's absolute minima).

2、Batch and Momentum

2.1、Batch batch

A training epoch Divided into several batch, every last batch Can be used for loss function parameters $\theta$ updated . Every epoch Of batch Will be reassigned .

2.2、Small Batch v.s. Large Batch

2.2.1、 Calculation speed

use GPU Parallel computing , The time consumption of small batch and large batch is basically the same within a certain range ：

But it's different batch It takes more time to switch between , So small batches epoch It takes longer ：

2.2.2、 Training optimization effect

Large batch training , It is easy to cause optimization errors （Optimization Fails）; Small batch training performance is better ：

reason ： The number of parameter updates in large batches is less , Low fault tolerance ; The number of small batch parameter updates is more , There are more possibilities to jump out local minima.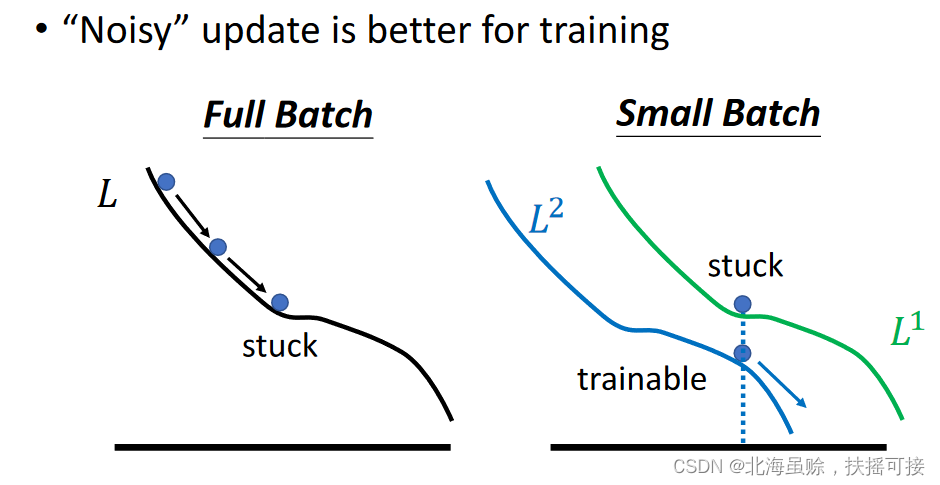

2.2.3、 Test the results

Small batch test data is better , The experimental results are as follows ：SB Indicates a small batch ,LB Indicates a large batch .

The reason is still the problem of parameter update ,train And test Loss function of , Think there is a certain translation ; Small batches are more likely to fall into Sharp Minima, Cannot update ：

2.2.4、 Comprehensive comparison

2.3、Momentum

Momentum： Learning rate momentum , When updating parameters , Consider not only the gradient of the function , Also consider the previously updated gradient directions ：
$${\mathbf{m}}^t=\lambda {\mathbf{m}}^{t-1}-\eta {\mathbf{g}}^{t-1}$$
Consider gradient descent and learning rate momentum , The parameters are updated as follows ：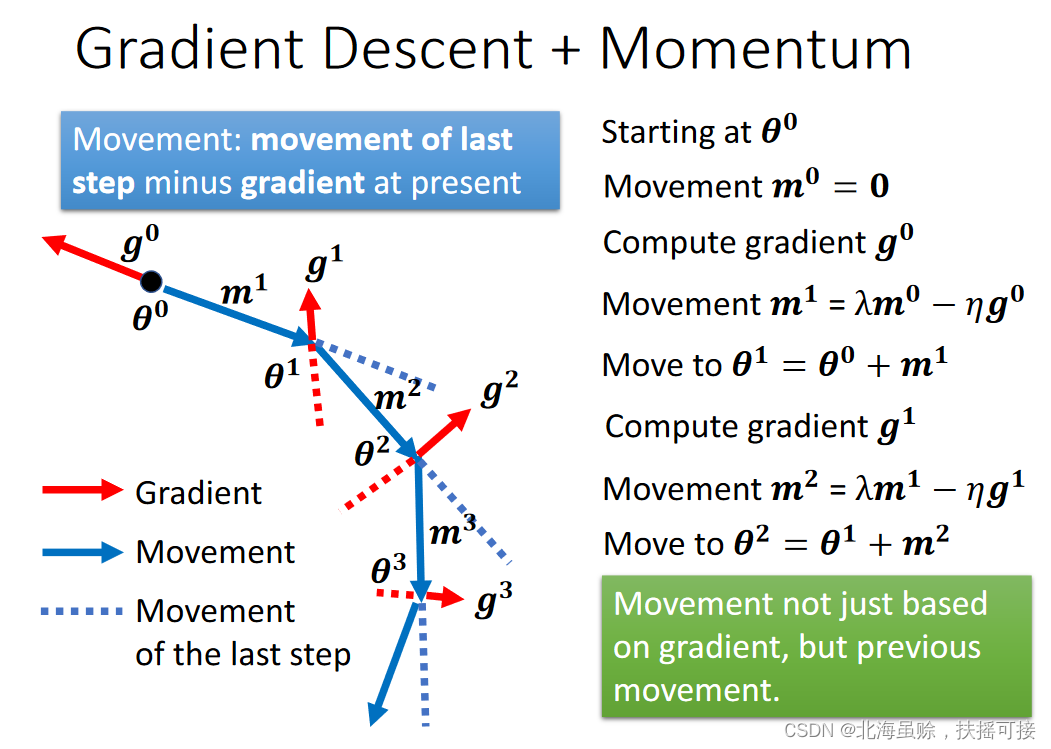
In calculation , You can find , momentum $m^i$ contain $g^0$ To $g^i$ The sum of the weights of ;
$${\mathbf{m}}^i=-({\lambda }^{i-1}\eta g^0+{\lambda }^{i-2}{\eta }^2{g}^1+...+\lambda {\eta }^{i-1}{g}^{i-2})-\eta g^{i-1}$$

3、 Conclusion

• critical point Critical points The exit gradient is 0.
• The critical points can be saddle points and local minima .
  It can be determined by the haisai matrix H decision .
  You can escape the saddle point in the direction of the eigenvector of the Hessian matrix .
  Local minima may be rare .
• Small batches and momentum updates help escape the tipping point .