当前位置:网站首页>【Image Processing】空间域图像增强
【Image Processing】空间域图像增强
2022-06-11 08:29:00 【Jeff_zvz】

Catalogue
空间域图像增强
Introduction
空间域分为单独的像素点处理和邻域处理。像素点处理每次处理一个像素,且只关注这个像素且与邻域无关,邻域处理一般就是滤波卷积,本质就是图像和掩码做卷积。
像素点处理
像素点处理就是映射: Z = T ( r ) \Zeta = \Tau(r) Z=T(r)
灰度变换
恒等变换
Z = r \Zeta = r Z=r
反转变换
Z = L − r \Zeta = L - r Z=L−r
def inverse_transform(img):
p_max = np.max(np.max(img))
out = p_max - img
return out
对数变换
Z = c ∗ log 2 r + 1 \Zeta = c*\log_{2}^{r+1} Z=c∗log2r+1
或
Z = c ∗ log v + 1 1 + v ∗ r \Zeta = c*\log_{v+1}^{1+v*r} Z=c∗logv+11+v∗r
对数变换可以将图像的低灰度值部分扩展,显示出低灰度部分更多的细节,将其高灰度值部分压缩,减少高灰度值部分的细节,从而达到强调图像低灰度部分的目的。
对数变换实现了扩展低灰度值而压缩高灰度值的效果,广泛应用于频谱图像的显示中。对数变换的典型应用是傅立叶频谱的动态范围很宽,直接显示时受显示设备动态范围的限制而丢失大量的暗部细节;使用对数变换将图像的动态范围进行非线性压缩后,就可以清晰地显示。
def image_log(img):
img_c = img/255.
return np.uint8(np.log(1+img_c) *255)
def img_log(v,img):
img_c = img/255.
return np.uint8(np.log(1+v*img_c)/np.log(v+1) * 255)
幂律变换(伽马变换)
Z = c ∗ ( r + a ) γ \Zeta = c*(r+a)^γ Z=c∗(r+a)γ
伽马变换本质上是对图像矩阵中的每个值进行幂运算。0< γ<1时,拉伸图像中灰度级较低的区域,压缩灰度级较高的部分,增加图像的对比度;γ > 1时,拉伸图像中灰度级较高的区域,压缩灰度级较低的部分,降低图像的对比度。
伽马变换通过非线性变换对人类视觉特性进行补偿,最大化地利用有效的灰度级带宽。很多拍摄、显示、打印设备的亮度曲线都符合幂律曲线,因此伽马变换广泛应用于各种设备显示效果的调校,称为伽马校正。

def gamma_transform(img,gamma=2,eps=0):
return 255*(((img+eps)/255.)**gamma)
分段变换
使用掩码来分段,然后分段处理。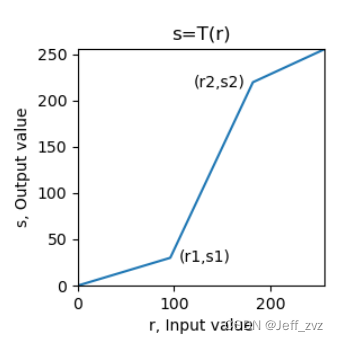
def fenduan(img,x1,x2,y1,y2):
if x1==x2 or x2==255:
return None
#掩码
m1 = (img<x1)
m2 = (img>=x1)& (img <= x2)
m3 = (img>x2)
out = (img*y1/x1)*m1 + (((img-x1)*(y2-y1)/(x2-x1))+y1)*m2 \
+(((255-y2)*(img-x2)/(255-x2))+y2)*m3
return out
也可以使用灰度级进行分层
imgLayer1[(imgLayer1[:,:]<a) | (imgLayer1[:,:]>b)] = 0 # 其它区域:黑色
imgLayer1[(imgLayer1[:,:]>=a) & (imgLayer1[:,:]<=b)] = 255 # 灰度级窗口:白色
阈值变换
Z = { z 1 , x ≤ t h 1 z 2 , x > t h 2 (1) \Zeta= \begin{cases} z1,\quad x\leq th1\\ z2, \quad x>th2 \end{cases} \tag{1} Z={ z1,x≤th1z2,x>th2(1)
低于某个阈值,变成z1;高于某个阈值,变成z2。cv2.threshold(src,thresh,maxval,type[,dst])->retval, dst
- scr:变换操作的输入图像,nparray 二维数组,必须是单通道灰度图像!
- thresh:阈值,取值范围 0~255
- maxval:填充色,取值范围 0~255,一般取 255
- type:变换类型
cv2.THRESH_BINARY:大于阈值时置 255,否则置 0
cv2.THRESH_BINARY_INV:大于阈值时置 0,否则置 255
cv2.THRESH_TRUNC:大于阈值时置为阈值 thresh,否则不变(保持原色)
cv2.THRESH_TOZERO:大于阈值时不变(保持原色),否则置 0
cv2.THRESH_TOZERO_INV:大于阈值时置 0,否则不变(保持原色)
cv2.THRESH_OTSU:使用 OTSU 算法选择阈值- 返回值 retval:返回二值化的阈值
- 返回值 dst:返回阈值变换的输出图像
直方图处理
直方图
直方图是一个展示各级灰度个数的图表。
归一化直方图将其归一化,显示其概率分布。
def hist(img_c):
r,c = img_c.shape
img_c = img_c.flatten() #展平
img_c = img_c.tolist()
myhist = [img_c.count(i)/(r*c) for i in range(256)] #归一化
return myhist
opencv中函数cv2.calcHist(images, channels, mask, histSize, ranges[, hist[, accumulate ]]) → hist
images:输入图像,用 [] 括号表示
channels: 直方图计算的通道,用 [] 括号表示,灰度图为0
mask:掩模图像,一般置为 None
histSize:直方柱的数量,一般取 256
ranges:像素值的取值范围,一般为 [0,256]
返回值 hist:返回每一像素值在图像中的像素总数,形状为 (histSize,1)
直方图均衡化
直方图均衡化就是将不规则分布的灰度变成较规则且均衡地灰度分布。直方图均衡化的基本思想是对图像中占比大的灰度级进行展宽,而对占比小的灰度级进行压缩,使图像的直方图分布较为均匀,扩大灰度值差别的动态范围,从而增强图像整体的对比度。
概率论中有结论:
当有 Z = T (\r) 时,存在概率分布:
P z ( z ) = P r ( r ) ∗ ∣ d z ∣ / ∣ d r ∣ P_z(z) = P_r(r) * |dz|/|dr| Pz(z)=Pr(r)∗∣dz∣/∣dr∣
且易证得
T ( r ) = ( L − 1 ) ∗ ∫ 0 r P w ( w ) d w T(r) = (L-1) * \int_0^r P_w(w)dw T(r)=(L−1)∗∫0rPw(w)dw
离散形式
由上面证得的T(\r),且由图像是离散的,变换函数T(\r)是概率分布的累加,曲线类似于梯形单调递增。
def get_pdf(img): #概率密度分布
total = img.shape[0]*img.shape[1]
return [np.sum(img==i)/total for i in range(256)]
def hist_equal(img):
pdf = get_pdf(img)
out = np.copy(img)
s = 0.
Tr = [] # 变换函数
for i in range(256):
s = s+pdf[i]
out[(img==i)] = s*255.
Tr.append(s*255.)
out = out.astype(np.uint8)
return out,Tr
opencv函数cv2.equalizeHist(src[, dst]) → dst
直方图匹配(直方图规范化)
假设图2的直方图效果就是我们想要的直方图,我们的原图为图1。已知我们可以直方图均衡化将图1、图2都变成过度直方图,由变换函数我们可以得到图2到过度直方图的映射表,从而我们可以逆映射回图2.

def get_pdf(img): #概率密度分布
total = img.shape[0]*img.shape[1]
return [np.sum(img==i)/total for i in range(256)]
def hist_equal(img):
pdf = get_pdf(img)
out = np.copy(img)
s = 0.
Tr = [] # 变换函数
for i in range(256):
s = s+pdf[i]
out[(img==i)] = s*255.
Tr.append(s*255.)
out = out.astype(np.uint8)
return out,Tr
def gen_eq_pdf(): #生成均匀分布,我们想要的直方图
return [0.0039 for i in range(256)] # 1/256 = 0.0039
def gen_target_table(Pv): #Pv为构建好的概率分布直方图
table = []
#下面一段代码就是执行G变换,均衡化(纵轴)映射到理想直方图(横轴)
SUMq = 0.
for i in range(256): #已知灰度值都是从0到255,通过变换函数,映射到纵轴,形成映射表
SUMq = SUMq + Pv[i]
table.append(np.round(SUMq*255,0)) #四舍五入
return table
def hist_specify(img):
Pv = gen_eq_pdf()
table = gen_target_table(Pv)
ori_img,T_trans = hist_equal(img) #ori_img就是B'
out = ori_img.copy() #构造输出图像
map_val = 0 #逆映射值初始化为0
for v in range(256):
if v in ori_img:
if v in table:
map_val = len(table)-table[::-1].index(v)-1 #找到,取最大一个
out[(ori_img == v)] = map_val #找不到逆映射关系,取前一个
return out
局部直方图均衡化
直方图均衡和直方图匹配都是基于整幅图像的灰度分布进行全局变换,并非针对图像局部区域的细节进行增强。
直方图处理对于局部同样适用,局部直方图处理的思想是基于像素邻域的灰度分布进行直方图变换处理。
过程:
(1)设定某一大小的模板(矩形邻域),在图像中沿逐个像素移动;
(2)对每个像素位置,计算模板区域的直方图,对该局部区域进行直方图均衡或直方图匹配变换,变换结果只用于模板区域中心像素点的灰度值修正;
(3)模板(邻域)在图像中逐行逐列移动,遍历所有像素点,完成对整幅图像的局部直方图处理。
opencv函数:cv2.createCLAHE([, clipLimit[, tileGridSize]]) → retval
- clipLimit:颜色对比度的阈值,可选项,默认值 8
- titleGridSize:局部直方图均衡化的模板(邻域)大小,可选项,默认值 (8,8)
cv2. createCLAHE 是一种限制对比度自适应直方图均衡化方法(Contrast Limited Adaptive Hitogram Equalization),采用了限制直方图分布的方法和加速的插值方法。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('img/low_pix.jpg',0)
imgequ = cv2.equalizeHist(img)
clahe = cv2.createCLAHE(clipLimit=2.0,tileGridSize=(4,4))
imglocalequ = clahe.apply(img)
plt.figure(figsize=(9, 6))
plt.subplot(131), plt.title('Original'), plt.axis('off')
plt.imshow(img, cmap='gray', vmin=0, vmax=255)
plt.subplot(132), plt.title(f'Global Equalize Hist'), plt.axis('off')
plt.imshow(imgequ, cmap='gray', vmin=0, vmax=255)
plt.subplot(133), plt.title(f'Local Equalize Hist'), plt.axis('off')
plt.imshow(imglocalequ, cmap='gray', vmin=0, vmax=255)
plt.tight_layout()
plt.show()

空间滤波
图像滤波是在尽可能保留图像细节特征的条件下对目标图像的噪声进行抑制,是常用的图像预处理操作。
图像平滑滤波
平滑滤波也称为低通滤波,可以抑制图像中的灰度突变,使图像变得模糊,是低频增强的空间域滤波技术
均值滤波

均值滤波就是将邻域内像素值的平均值来替代中间值,其副作用就是会让图像变得模糊(模糊边缘),且卷积核越大模糊得越严重。
从数学角度来说,是因为均值滤波会受到邻域点影响,边缘是变化很突兀的点,所以均值滤波卷积之后这一区域的像素值变得平滑,图像上呈现出来就是变得模糊。
以下为均值滤波处理噪声之后,阈值化处理。
代码:dst=cv2.blur(src ,ksize, anchor, borderType)
中值滤波
中值滤波是一种非线性平滑技术,是基于统计排序方法的滤波器,其将掩码内的像素值按一维排序,然后取中间值作为当前像素值。其和均值滤波相比最大的特点就是,这是一种保边缘的滤波,取代的值是图像原有的值。且可以消去孤立点,对椒盐噪声效果最好。
代码:dst=cv2.medianBlur(src,ksize)
双边滤波
双边滤波是一种结合空间邻近度和像素值相似度的折中方法,同时考虑空域信息和灰度相似性,去噪同时有效保持边缘,对于人像有美颜效果。
边缘灰度变化大,高斯滤波会明显地模糊边缘,对高频信息保护弱。双边滤波在高斯滤波基础上加入了像素强度差异的高斯方差,在边缘附近较远的像素对边缘上像素值影响不大,从而实现边缘保护。
双边滤波不能很好地过滤彩色图中高频噪声。
其数学公式如下:
opencv函数:cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]]) → dst
参数说明:
- src:输入图像,可以是灰度图像,也可以是多通道的彩色图像
- dst:输出图像,大小和类型与 src 相同
- d:滤波核的像素邻域直径。如 d<=0 ,则由从 sigmaSpace 计算得到。
- sigmaColor:滤波器核在颜色空间的方差,反映产生颜色影响的颜色强度区间的大小
- sigmaSpace:滤波器核在坐标空间的方差,反映产生颜色影响的影响空间的大小
- borderType:边界扩充的类型
导向滤波
导向滤波又称引导滤波,通过一张引导图片反映边缘、物体等信息,对输入图像进行滤波处理,使输出图像的内容由输入图像决定,但纹理与引导图片相似。
导向滤波的原理是局部线性模型,在保持双边滤波的优势(有效保持边缘,非迭代计算)的同时计算速度很快,从而克服双边滤波速度慢的缺点。
opencv函数:cv2.ximgproc_guidedFilter.filter(guide, src, d[, eps[, dDepth]) → dst
参数说明:
- src:输入图像,可以是灰度图像,也可以是多通道的彩色图像
- guide:导向图像,大小和类型与 src 相同
- dst:输出图像,大小和类型与 src 相同
- d:滤波核的像素邻域直径
- eps:规范化参数, eps 的平方类似于双边滤波中的 sigmaColor
- dDepth:输出图片的数据深度
图像锐化滤波
图像模糊通过平滑(加权平均)来实现,类似于积分运算。图像锐化则通过微分运算(有限差分)实现,使用一阶微分或二阶微分都可以得到图像灰度的变化值。
图像锐化的目的是增强图像的灰度跳变部分,使模糊的图像变得清晰。图像锐化也称为高通滤波,通过和增强高频,衰减和抑制低频。图像锐化常用于电子印刷、医学成像和工业检测。
- 恒定灰度区域,一阶导数为零,二阶导数为零;
- 灰度台阶或斜坡起点区域,一阶导数非零,,二阶导数非零;
- 灰度斜坡区域,一阶导数非零,二阶导数为零。
掩码与求导:
图像中,x和y方向的求导(梯度)可以通过差分来表示(因为图像是离散的),既 ∂ f ∂ x = f ( x + 1 , y ) − f ( x , y ) \frac{\partial f}{\partial x} = f(x+1,y) - f(x,y) ∂x∂f=f(x+1,y)−f(x,y)
其掩码为
二阶导数为
∂ 2 f ∂ x 2 = f ( x − 1 , y ) + f ( x + 1 , y ) − 2 f ( x , y ) \frac{\partial ^2 f}{\partial x^2} = f(x-1,y) + f(x+1,y) - 2f(x,y) ∂x2∂2f=f(x−1,y)+f(x+1,y)−2f(x,y)
掩码为
拉普拉斯算子
Δ f = ∂ 2 f ∂ y 2 + ∂ 2 f ∂ x 2 = f ( x − 1 , y ) + f ( x + 1 , y ) + f ( x , y − 1 ) + f ( x , y + 1 ) − 4 f ( x , y ) \Delta f= \frac{\partial ^2 f}{\partial y^2}+\frac{\partial ^2 f}{\partial x^2} = f(x-1,y) + f(x+1,y) + f(x,y-1) + f(x,y+1) - 4f(x,y) Δf=∂y2∂2f+∂x2∂2f=f(x−1,y)+f(x+1,y)+f(x,y−1)+f(x,y+1)−4f(x,y)
掩码为:

拉普拉斯算子是一个二阶导数算子,利用二次微分特性和峰值间过零点来确定边缘的位置,对奇异点或边缘点更为敏感。
dst = cv2.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])
def Laplace(img):
edge = cv2.Laplacian(img,-1,ksize=3)
edge = cv2.convertScaleAbs(edge)
e_edge = cv2.equalizeHist(edge)
out = img + e_edge
plt.subplot(221)
plt.imshow(img,cmap='gray')
plt.title('original')
plt.subplot(222)
plt.imshow(edge,cmap='gray')
plt.title('edge')
plt.subplot(223)
plt.imshow(e_edge,cmap='gray')
plt.title('Edge enhanced')
plt.subplot(224)
plt.imshow(out,cmap='gray')
plt.title('ruihua')
plt.show()

钝化掩蔽
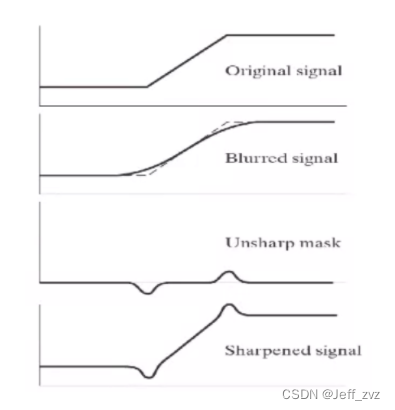
def func(img):
blur = cv2.blur(img,(5,5))
unsharp = img - blur
out = img + unsharp
plt.subplot(221)
plt.imshow(img,cmap='gray')
plt.title('original')
plt.subplot(222)
plt.imshow(blur,cmap='gray')
plt.title('blur')
plt.subplot(223)
plt.imshow(unsharp,cmap='gray')
plt.title('unsharp')
plt.subplot(224)
plt.imshow(out,cmap='gray')
plt.title('fanruihua')
plt.show()

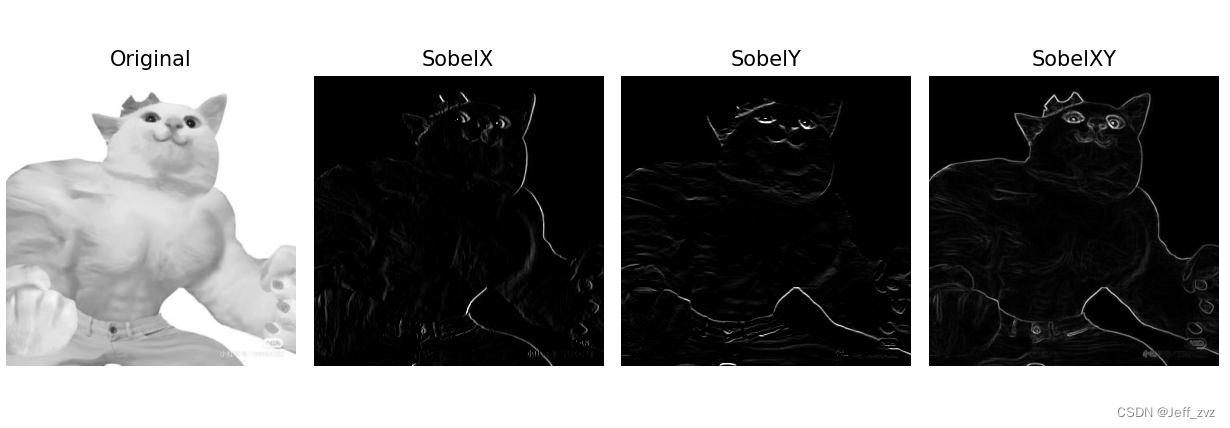
sobel算子
Sobel 算子是一种离散的微分算子,是高斯平滑和微分求导的联合运算,抗噪声能力强。
Sobel 梯度算子利用局部差分寻找边缘,计算得到梯度的近似值。先计算水平、垂直方向的梯度,再求总梯度。编程实现时,可以用绝对值近似平方根:G = ∣ G x ∣ + ∣ G y ∣
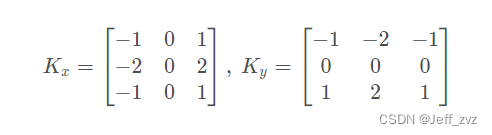
opencv函数:cv2.Sobel(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]]) → dst
参数说明:
- src:输入图像,灰度图像,不适用彩色图像
- dst:输出图像,大小和类型与 src 相同
- ddepth:输出图片的数据深度,由输入图像的深度进行选择
- dx:x 轴方向导数的阶数,1 或 2
- dy:y 轴方向导数的阶数,1 或 2
- ksize:Sobel 卷积核的大小,可选的取值为:1/3/5/7,ksize=-1 时使用Scharr 算子运算
- scale:缩放比例因子,可选项,默认值为 1
- delta:输出图像的偏移量,可选项,默认值为 0
- borderType:边界扩充的类型,注意不支持对侧填充(BORDER_WRAP)
def sobel(img):
SobelX = cv2.Sobel(img, cv2.CV_16S, 1, 0) # 计算 x 轴方向
SobelY = cv2.Sobel(img, cv2.CV_16S, 0, 1) # 计算 y 轴方向
absX = cv2.convertScaleAbs(SobelX) # 转回 uint8
absY = cv2.convertScaleAbs(SobelY) # 转回 uint8
SobelXY = cv2.addWeighted(absX, 0.5, absY, 0.5, 0) # 用绝对值近似平方根
plt.figure(figsize=(10, 6))
plt.subplot(141), plt.axis('off'), plt.title("Original")
plt.imshow(img, cmap='gray', vmin=0, vmax=255)
plt.subplot(142), plt.axis('off'), plt.title("SobelX")
plt.imshow(SobelX, cmap='gray', vmin=0, vmax=255)
plt.subplot(143), plt.axis('off'), plt.title("SobelY")
plt.imshow(SobelY, cmap='gray', vmin=0, vmax=255)
plt.subplot(144), plt.axis('off'), plt.title("SobelXY")
plt.imshow(SobelXY, cmap='gray')
plt.tight_layout()
plt.show()
边栏推荐
- Project training - clonemon
- Zipkin入门
- These gadgets are also very easy to use
- Modifying field length in Oracle and postgrepsql
- Collation of open source modulation identification data set
- XXL task executor calls local project
- Typescript class and interface, class and generic, interface merging
- 这几个小工具也太好用了
- Introduction to database system experiment report answer Experiment 6: advanced query of data table
- Heap can also be regarded as a tree structure. It is specified that the root node must be greater than or less than the left and right child nodes, but the size order of the left and right child nodes
猜你喜欢
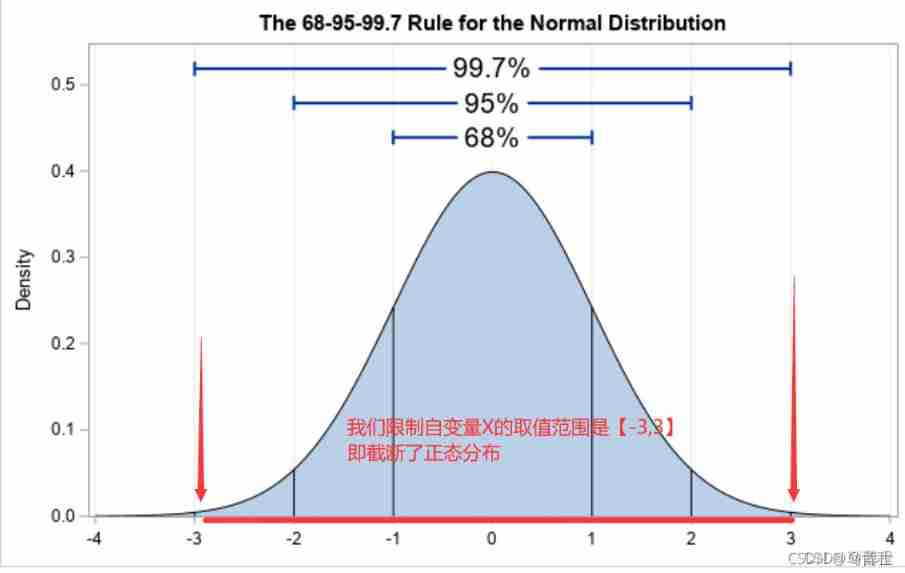
TRUNC in pytorch_ normal_ principle

【CVPR2022】QueryDet论文精读

盘它!用「飞项」轻松管理各类型项目

Anaconda+tensorflow most effective summary version (blood and tears summary of 6 reloads)

进程间的通信

【clickhouse专栏】新建库角色用户初始化

torch. nn. functional. pad

mysql高级特性篇,可以多看看,应付面试

Redis cluster in Linux system

Don't want the project out of control? You need to use project management tools
随机推荐
项目实训-克隆门
(resolved) the tqdm progress bar in the Jupiter notebook does not update and display in one line, but scrolls down to output
Typescript type alias
MySQL死锁问题如何解决?背诵版
CentOS essay 03:centos8.2 installing MySQL
for in / for of / forEach 循环
Typescript recognizable Union
Don't want the project out of control? You need to use project management tools
GO语言:字符串的连接、数字转化字符串
Interprocess communication
Collation of open source modulation identification data set
Disk format FAT32, exFAT, NTFS of [software tool]
指定环境下安装Jupyter
Is the result too different from the goal? With the help of target management, you can reach the target accurately!
Entity class conversion cannot be reassigned
Web design and website planning assignment 11 game selection form
ActiveMQ简单教程,适合初学者,学习笔记yyds
Empty difference between postgrepsql and Oracle
字符设备驱动程序之异步通知机制
Project training - clonemon


